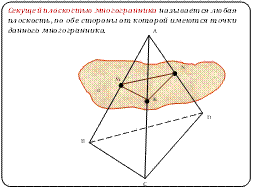
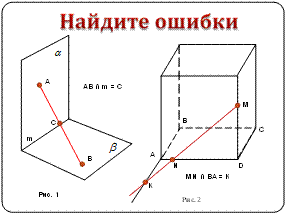
Если две точки принадлежат секущей плоскости и плоскости некоторой грани многогранника, то прямая, проходящая через данные точки, будет являться следом секущей плоскости на плоскости грани.
Если секущая плоскость параллельна прямой, лежащей в некоторой плоскости, и пересекает эту плоскость, то линия пересечения этих плоскостей параллельна данной прямой.
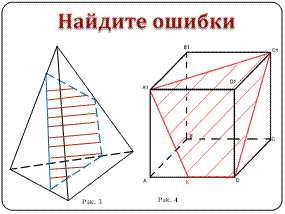
При пересечении двух параллельных плоскостей секущей плоскостью получаются параллельные прямые.
Если секущая плоскость параллельна некоторой плоскости, то эти две плоскости пересекают третью плоскость по прямым, параллельным между собой.
Если у секущей плоскости и плоскостей двух пересекающихся граней есть общая точка, то она лежит на прямой, содержащей общее ребро данных граней.
Задания для практической работы
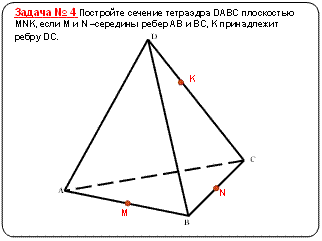
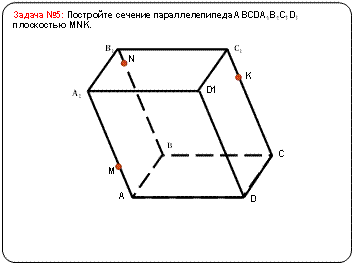
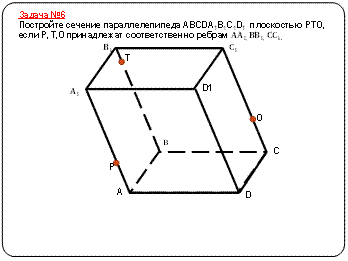
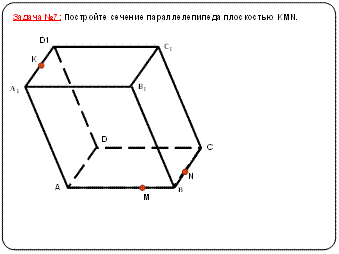
Творческие задания (карточки по вариантам):
1. В правильной треугольной пирамиде SАВС через вершину С и середину ребра SА проведите сечение пирамиды, параллельное SB. На ребре АВ взята точка F так, что АF:FВ=3:1. Через точку F и середину ребра SС проведена прямая. Будет ли эта прямая параллельна плоскости сечения?
2. АВ1С - сечение прямоугольного параллелепипеда АВСDА1В1С1D1. Через точки Е, F, К, которые являются соответственно серединами ребер DD1, А1D1, D1C1 проведено второе сечение. Докажите, что треугольники ЕFК и АВ1C подобны, и установите какие углы этих треугольников равны между собой.
Практическое занятие 13
Выполнение заданий на признаки перпендикулярности прямой и плоскости, перпендикулярности плоскостей
Цель:
1) Обобщить теоретические знания по теме: «Перпендикулярность прямых. Перпендикулярность прямой и плоскости».
2) Рассмотреть алгоритмы решений заданий теме «Перпендикулярность прямых. Перпендикулярность прямой и плоскости», решить задачи.
3) Формировать умения прогнозировать собственную деятельность, умение организовать свою деятельность и анализировать ее.
Теоретический материал
Определение Прямая, пересекающая плоскость, называется перпендикулярной этой плоскости, если она перпендикулярна каждой прямой, которая лежит в данной плоскости и проходит через точку пересечения.
Теорема 1 ПРИЗНАК ПЕРПЕНДИКУЛЯРНОСТИ ПРЯМОЙ И ПЛОСКОСТИ. Если прямая, пересекающая плоскость, перпендикулярна двум прямым в этой плоскости, проходящим через точку пересечения данной прямой и плоскости, то она перпендикулярна плоскости.
Теорема 2 1-ое СВОЙСТВО ПЕРПЕНДИКУЛЯРНЫХ ПРЯМОЙ И ПЛОСКОСТИ. Если плоскость перпендикулярна одной из двух параллельных прямых, то она перпендикулярна и другой.
Теорема 3 2-ое СВОЙСТВО ПЕРПЕНДИКУЛЯРНЫХ ПРЯМОЙ И ПЛОСКОСТИ. Две прямые, перпендикулярные одной и той же плоскости, параллельны.
Пример 1: Докажите, что через любую точку прямой в пространстве можно провести перпендикулярную ей прямую.
Решение: пусть а - прямая и А - точка на ней. Возьмем любую точку Х вне прямой а и проведем через эту точку и прямую а плоскость . В плоскости через точку А можно провести прямую b, перпендикулярную а.
Пример 2: Докажите, что через любую точку А можно провести прямую, перпендикулярную данной плоскости.
Решение: Проведем в плоскости две пересекающиеся прямые с и b. Через точку их пересечения проведем плоскости и перпендикулярные прямым b и соответственно. Они пересекаются по некоторой прямой а. Прямая а перпендикулярна прямым b и с, значит и плоскости. Проведем теперь через точку А прямую d, параллельную а. По теореме 2 она перпендикулярна плоскости .
Пример 3: Докажите, что если прямая параллельна плоскости, то все ее точки находятся на одинаковом расстоянии от плоскости.
Решение: Пусть а - данная прямая и - данная плоскость. Возьмем на прямой а две произвольные точки Х и Y. Их расстояния до плоскости - это длины перпендикуляров ХХ1и YY1, опущенных на эту плоскость. По теореме 3 прямые ХХ1 и YY1 параллельны, следовательно, лежат в одной плоскости. Эта плоскость пересекает плоскость по прямойХ1Y1.Прямая а параллельна прямой Х1Y1, так как не пересекает содержащую её плоскость. Итак у четырехугольника ХХ1YY1противолежащие стороны параллельны. Следовательно, он параллелограмм, а значитХХ1=YY1.
Задачи для самостоятельного решения
Задача №1: Плоскости равностороннего треугольника АВС и квадрата ВСDE перпендикулярны. Найдите расстояние от точки А до стороны DE, если АВ.
Задача №2: Диагональ ВD ромба АВСD перпендикулярна к плоскости α. Как расположена по отношению к этой плоскости другая её диагональ?
Задача №3: Верхние концы двух вертикально стоящих столбов, удаленных на расстояние 4 м, соединены перекладиной. Высота одного столба 5 м, а другого - 8 м. Найдите длину перекладины.
Задачи на готовых чертежах
Задание № 1
Дан куб ABCDA1B1C1D1.
Доказать:
1) прямые AC и D1O перпендикулярны;
2)  ABC1 = 90°
| 
|
| Задание № 2
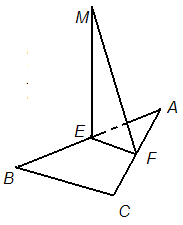
Отрезок EF является средней линией прямоугольного треугольника ABC ( 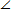ACB=90°). Через точку E проведен перпендикуляр ME к плоскости этого треугольника.
Доказать:
1) MF⊥AC,
2) MC = MA.
| 
|
Дополнительные задания (по вариантам)
| 1 вариант | 2 вариант |
1.
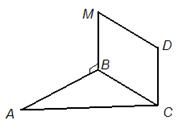Дано: M  ABC, MBCD – прямоугольник.
Доказать: прямая CD⊥ABC
| 1.
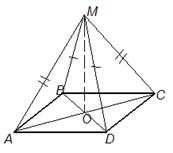Дано: ABCD – параллелограмм.
Доказать: прямая MO⊥ABC
|
2.
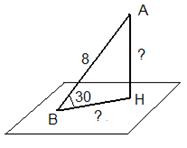Дано: AH ⊥α, AB – наклонная.
Найти AH, BH.
| 2.
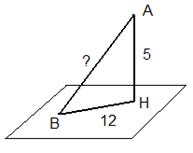Дано: AH ⊥α, AB – наклонная.
Найти AB.
|
Работа в парах – решаются задачи по готовым чертежам.
| 1 группа | 2 группа |
Дано:
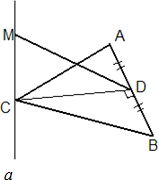a⊥ABC
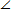AСВ = 90°,
AC = 4, MD = 3.
Найти MC.
| Дано:
a ⊥ABC,
ΔABC - равносторонний,
AB = 2√3, MD = 4
Найти MC.
|
Практическое занятие №14
Определение угла между прямой и плоскостью. Применение теоремы о трёх перпендикулярах
Цели: совершенствовать умения учащихся применять теоретические знания к решению задач на доказательство и вычисления, развивать пространственное воображение, развивать умение строить аргументированное и логически верное решение задачи, способствовать дальнейшему развитию навыков самоконтроля.
I.
1. Дано: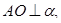 
АО = 4,
p – касательная к окружности,
АВ – наклонная к α, АВ = 5
Доказать: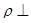 
АВ
Найти: r
М
2. Дано: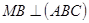 
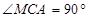
Доказать: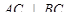 
В
С
А
D
3. Дано: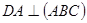 
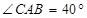
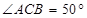
Доказать: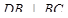 
C
A
B
В
4. Дано: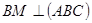 
ВК – медиана и высота ∆ АВС
Доказать: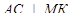 
Определить вид ∆ АМС В С
К
А
II.
1. Дано: ВК – высота ∆ АВС М
АВ = 7, ВС = 3
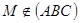, МВ = 4
АМ =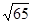 
, СМ = 5 В С
Доказать: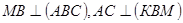 
2. Дано: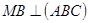 
, МВ = 3 К
МА = МС = 5, А
АК = КС,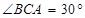 
Найти расстояние от точки М до АС.
3. Дано: ∆ АВС,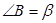 
, 
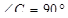Д
, 
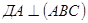
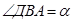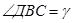
Доказать: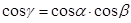 
4. Дано: ∆ АВС, 
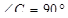, В А
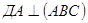
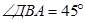С
Найти: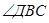 
Далее проводится проверка и обсуждение решения задач со всеми учащимися класса
Решение задач:
№ 1
1) ∆ МВС – прямоугольный, так как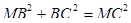 
(4² + 3² = 5²), следовательно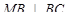 
2) ∆ МВА – прямоугольный, так как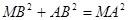 
(4² + 7² = 
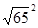), следовательно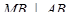 
3) Из 1) и 2) следует, что МВ – перпендикуляр к плоскости АВС.
4) МК – наклонная к плоскости АВС, ВК – её проекция,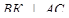 
, следовательно 
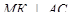. Тогда прямая АС перпендикулярна двум пересекающимся прямым МК и ВК плоскости МВК, т.е. 
Что и требовалось доказать.
№ 2
1) Так как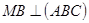 
, 
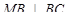и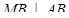 
. Тогда ∆ АВМ = ∆СВМ по катету и гипотенузе (МВ – общий катет, МА = МС по условию), следовательно АВ = СВ =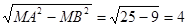 
2) ∆АВС: АВ = СВ = 4,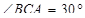 
, ВК – медиана, высота и биссектриса, следовательно ∆АВК – прямоугольный с гипотенузой 4 и острым углом 
,
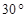ВК = 2
3) ВК – проекция МК на плоскость (АВС),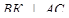 
, следовательно 
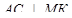, т.е. МК – расстояние от точки М до АС.
4) ∆ МВК – прямоугольный (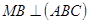 
). 
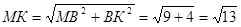
Ответ: расстояние от точки М до АС равно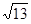 
№ 3
1) 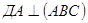, ДС – наклонная к плоскости АВС, АС – её проекция, 
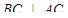(по условию), тогда 
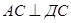, ∆ ДСВ – прямоугольный,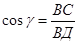 
2) ∆ АВС – прямоугольный по условию,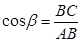 
3) ∆ ДАВ – прямоугольный ( ),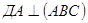 
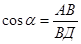
4) 
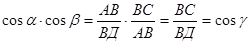, что и требовалось доказать.
№ 4
Используем формулу, доказанную в задаче № 3, cos ÐДВС = cos ÐДВА ∙ cos ÐАВС
cosÐДВС =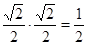 
, Ð ДВС =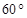 
Ответ: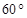
III. Задачи для самостоятельного решения:
Уровень 1
1) Через вершину В прямоугольника АВСД проведен перпендикуляр МВ к плоскости прямоугольника. Определите вид ∆ АМД и найдите его площадь, если стороны прямоугольника АВ = 3 и АД = 8, а ВМ = 4. (Ответ: 20)
2) Из вершины равностороннего треугольника АВС восставлен перпендикуляр АД к плоскости треугольника. Найдите расстояние от точки Д до стороны ВС, если
АД = 13, ВС = 6. (Ответ: 14)
Уровень 2
1) К плоскости треугольника из центра вписанной в него окружности восставлен перпендикуляр длиной 3. Найдите расстояние от конца этого перпендикуляра до сторон треугольника, если длины сторон треугольника 13, 14 и 15 (Ответ: 5)
2) Точка М лежит вне плоскости ромба АВСД на равном расстоянии от его сторон. Найдите расстояние от проекции точки М на эту плоскость до сторон ромба, если сторона ромба равна 12, а острый угол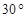 
(Ответ: 6)
Уровень 3
1) Катеты прямоугольного треугольника равны 18 и 32. Из точки М, делящей гипотенузу пополам, восставлен к плоскости треугольника перпендикуляр МК, равный 12. Найдите расстояние от точки К до каждого катета. ( Ответ: 20 и 15)
Через вершину А прямоугольного треугольника АВС в прямым углом В проведён перпендикуляр АД к плоскости треугольника. Найдите длину наклонной ДС, если её проекция равна ℓ,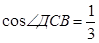 
, 
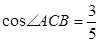. (Ответ: 
ℓ)
Практическое занятие №15
Определение перестановок, размещений, сочетаний при решении задач
Цель работы: закрепить знания и навыки в решении комбинаторных задач
Умение и навыки, которые должны приобрести студенты на занятии: вычислять сочетания, размещения, перестановки.
Дата: 2018-12-21, просмотров: 741.
