Выполнение заданий на построение графиков тригонометрических функций
Цель
Постройте графики предложенных функций.
Выполнение работы
Методические указания.
На миллиметровой бумаге, формата А4. Постройте графики предложенных функций. Масштаб выберите 1 см. откладывая единичные отрезки по оси х, помните, что число π =3,14=3 см.
Каждый график изобразите на отдельной координатной плоскости.
Работа состоит из двух частей: первая часть, это задания которые обязательно нужно выполнить, чтобы получить зачет, если эти задания выполнены с ошибкой, необходимо их исправить и снова сдать работу на проверку. Вторая часть, содержит задания, выполнив которые, вы можете заработать дополнительную оценку: основная часть +2 задания – «4», основная часть +3 задания – «5».
Вторая часть рассчитана на 10 вариантов, номер варианта совпадает с последней цифрой порядкового номера в списке. Например, 1, 11, 21, 31 …выполняют 1 вариант, 2,12, 22 … - 2 вариант, и т.д.
Задачи для самостоятельного решения.
Обязательная часть
Задание 1. Постройте графики функций: (для всех вариантов) Оценивается правильность построения и аккуратность при выполнении построений.
1) 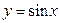 ,
,
2) 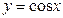
3) 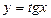
4) 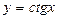
Задачи на дополнительную оценку:
Задание 2.Постройте графики функций, выполнив преобразования:
1-й вариант А)  Б)
Б) 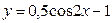 В)
В) 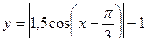
2-й вариант А) 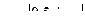 Б)
Б) 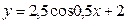 В)
В) 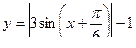
3-й вариант А)  Б)
Б) 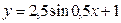 В)
В) 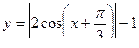
4-й вариант А)  Б)
Б) 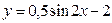 В)
В) 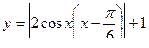
5-й вариант А) 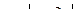 Б)
Б) 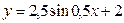 В)
В) 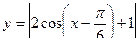
6-й вариант А) 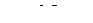 Б)
Б) 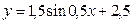 В)
В) 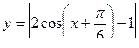
7-й вариант А)  Б)
Б) 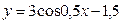 В)
В) 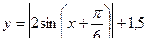
8-й вариант А)  Б)
Б) 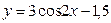 В)
В) 
9-й вариант А) 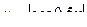 Б)
Б) 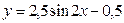 В)
В) 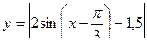
10-й вариант А)  Б)
Б) 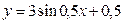 В)
В) 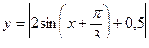
Сделайте выводы, ответив на вопросы.
1) Как называются графики тригонометрических функций?
2) Какие преобразования графиков функций вы знаете?
3) Как выполняется преобразование сжатия и растяжения относительно оси Х, относительно оси У?
Практическое занятие № 32
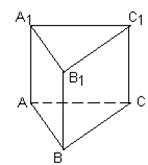
Выполнение построений прямой, наклонной призм, нахождение их элементов
Часть 1
| РАЗВЕРТКА | ЧЕРТЕЖ | ПОЛНАЯ ПОВЕРХНОСТЬ |

| 
| 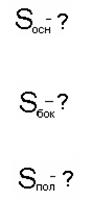
|
Задание № 1: По данным развёртки начертить на картоне, сделать модель многогранника. В тетради начертить модель и найти полную поверхность призмы.
Задание № 2: Перечертить таблицу в тетрадь и заполнить. Найти для каждого вопроса ответ, которые записаны под таблицей.
| Вопросы | Ответы | |
| Треугольная ПРИЗМА | ||
| 1 | Что такое треугольная призма? | |
| 2 | Как взаимно расположены боковые ребра призмы? | |
| 3 | Что можно сказать об основаниях призмы, боковых гранях? | |
| 4 | Определить элементы треугольной призмы. | |
| 5 | Сколько диагоналей у треугольной призмы? | |
Ответы:
1.Основания призмы есть равные треугольники, боковые грани – это параллелограммы, если призма прямая то грани – прямоугольники
2. Боковые ребра призмы равны и параллельны
3. Ребер – 9, вершин – 6, граней – 5
4. Многогранник составленный из двух равных треугольников , которые расположены в двух параллельных плоскостях и трех параллелограммов называется ….
5. Призма не имеет диагоналей
Задание № 3: Выбрать правильные ответы, из полученных букв составить слово, по которому вы узнаете, каких принципов нужно придерживаться в жизни.
| Вопросы | Ответы | |
| Треугольная ПРИЗМА | ||
| 1 | Многоугольники из которых составлены многогранники – это … | К) ребра П) грани В) вершины Г) высоты |
| 2 | Перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания называется… | О) высота Р) прямая В)грань Г) вершина |
| 3 | В треугольной призме можно провести диагональ. | А) да Н) нет |
| 4 | В основании треугольной призмы может лежать равнобедренный треугольник | И) да Б) нет |
| 5 | В правильной треугольной призме в основании лежит | С) равнобедренный треугольник М) равносторонний треугольник В) прямоугольный треугольник |
| 6 | Треугольная призма имеет ….ребер | Г) 6 Р) 5 А) 9 |
| 7 | Боковые грани прямой треугольной призмы… | О) квадраты б Т) прямоугольники В) треугольники |
| 8 | Если в основании прямой призмы лежит правильный многоугольник то призма называется… | Ю) треугольная Б) прямая В)наклонная Ь) правильная |
Часть 2
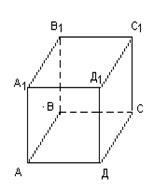
Задание № 1: По данным развёртки начертить на картоне, сделать модель многогранника. В тетради начертить модель и найти полную поверхность призмы.
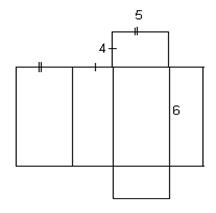
| 
| 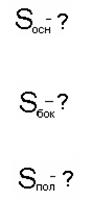
|
Задание № 2: Перечертить таблицу в тетрадь и заполнить. Найти для каждого вопроса ответ, которые записаны под таблицей.
| Четырехугольная ПРИЗМА | ||
| 1 | Что такое четырехугольная призма? | |
| 2 | Определить элементы четырехугольной призмы. | |
| 3 | Чем являются боковые грани призмы, основания четырехугольной призмы? | |
| 4 | Является ли параллелепипед призмой? | |
| 5 | Сколько диагоналей у четырехугольной призмы? | |
1. Основания призмы есть равные четырехугольники, боковые грани – это параллелограммы, если призма прямая то грани – прямоугольники
2. Параллелепипед – это призма, в основании которой лежит параллелограмм.
3. Ребер – 12, вершин – 8, граней – 6
4. Многогранник составленный из двух равных четырехугольников , которые расположены в двух параллельных плоскостях и четырех параллелограммов называется ….
5. В …. призме можно провести четыре диагонали.
Задание № 3: Выбрать правильные ответы, из полученных букв составить слово, по которому вы узнаете, каких принципов нужно придерживаться в жизни.
| Четырехугольная ПРИЗМА | ||
| 1 | Многогранник, который расположен по одну сторону от плоскости каждой его грани называется… | П) выпуклым Б) не выпуклым |
| 2 | В основании четырехугольной призмы может лежать ромб. | Р)да Б)нет |
| 3 | Сколько вершин имеет куб? | А)4 И) 8 О) 6 Ы) 12 |
| 4 | Правильная четырехугольная призма – в основании лежит | Р) ромб Н) квадрат В) прямоугольник |
| 5 | Прямоугольный параллелепипед – это призма | И)да А)нет |
| 6 | Боковые грани прямой четырехугольной призмы… | О) квадраты М) прямоугольники В) треугольники |
| 7 | Если боковые ребра призмы перпендикулярны к основаниям то призма… | Г)правильная А)прямая В) наклонная |
| 8 | Если в основании прямой призмы лежит правильный многоугольник то призма называется… | А) треугольная Д) прямая В)наклонная Т) правильная |
| 9 | Четырехугольная призма имеет ….ребер | А) 6 О) 5 Ю) 9 Ь) 12 |
Часть 3
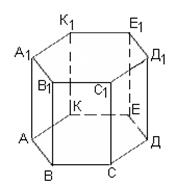
Задание № 1: По данным развёртки начертить на картоне, сделать модель многогранника. В тетради начертить модель и найти полную поверхность призмы.
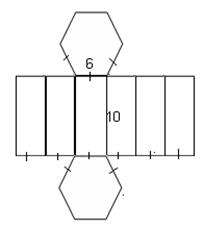
| 
| 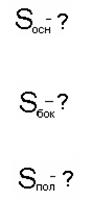
|
Задание № 2: Перечертить таблицу в тетрадь и заполнить. Найти для каждого вопроса ответ, которые записаны под таблицей.
| Шестиугольная ПРИЗМА | ||
| 1 | Что такое шестиугольная призма? | |
| 2 | Определить элементы шестиугольной призмы. | |
| 3 | Чем являются основания и боковые грани шестиугольной призмы ? | |
| 4 | Сколько диагоналей у шестиугольной призмы? | |
| 5 | Когда призма называется прямой? | |
1. Основания призмы есть равные шестиугольники, боковые грани – это параллелограммы, если призма прямая то грани – прямоугольники
2. В ….. призме можно провести 12 диагоналей.
3. Ребер – 18, вершин – 12, граней – 8.
4. Многогранник составленный из двух равных шестиугольников , которые расположены в двух параллельных плоскостях и шести параллелограммов называется ….
5. Если боковые ребра призмы перпендикулярны к основаниям то призма называется….
Задание № 3: Выбрать правильные ответы, из полученных букв составить слово, по которому вы узнаете, каких принципов нужно придерживаться в жизни.
| Шестиугольная ПРИЗМА | ||
| 1 | Грани - это многоугольники, из которых составлен многогранник | П)да Б)нет |
| 2 | Шестиугольная призма имеет ….ребер | Ю) 6 А) 5 И) 9 О) 18 |
| 3 | Боковые грани прямой шестиугольной призмы… | К) квадраты М) прямоугольники В) треугольники |
| 4 | Правильная шестиугольная призма – в основании лежит | А) ромб Р) квадрат Ю) прямоугольник О) правильный шестиугольник |
| 5 | В шестиугольной призме можно провести диагональ. | Г) да Б) нет |
| 6 | Если боковые ребра призмы перпендикулярны к основаниям то призма… | К)правильная А)прямая В) наклонная |
| 7 | Если в основании прямой призмы лежит правильный многоугольник то призма называется… | Р) шестиугольная Б) прямая В)наклонная Т) правильная |
| 8 | Куб – это шестиугольная призма | Ю) да Ь) нет |
Практическое занятие №33
Решение задач на определение элементов параллелепипеда и куба
Цель: закрепить навык решения практических задач на вычисление объёмов куба и прямоугольного параллелепипеда.
Теоретическая часть
За единицу измерения объема принимается объем единичного куба, т.е. объем куба, длина ребра которого равна 1 единице длины.
1 кубический сантиметр (1 cм3) - объем куба, длина которого равна 1 см.
1 кубический дециметр (1 дм3) - объем куба, длина которого равна 1 дм.
1 кубический метр (1 м3) - объем куба, длина которого равна 1 м.

Теорема: объем прямоугольного параллелепипеда с измерениями а, b, с вычисляется по формуле
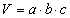 , V = Sосн
, V = Sосн  h.
h.
Теорема: объем наклонного (любого) параллелепипеда равен произведению площади основания S на высоту h:
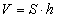 .
.
Объем куба равен кубу (третьей степени) его ребра. V = a3
Выполните задания
1 вариант
1. Выразите: а) в кубических дециметрах: 1 м3; 1 литр.
б) в кубических сантиметрах: 1 дм3; 1 м3.
2.Ответьте «да» или «нет».
а) Р = (а + b)  2 - периметр прямоугольника б) S = а
2 - периметр прямоугольника б) S = а 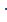 а - площадь квадрата
а - площадь квадрата
в) V = а 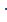 b
b 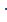 с - объем параллелепипеда г) V = а
с - объем параллелепипеда г) V = а  а
а  а - объём куба
а - объём куба
3. Объём каждого маленького кубика 1 куб. ед. Найдите объём фигур, изображённых на рисунках.

4  . Объём параллелепипеда равен 60 см3, если размеры 4см, 5см. Проставьте недостающий размер.
. Объём параллелепипеда равен 60 см3, если размеры 4см, 5см. Проставьте недостающий размер.
5. Каковы измерения параллелепипеда на рис. б), сложенного из 3 одинаковых брусков,  изображённых на рис. а). Каков его объём?
изображённых на рис. а). Каков его объём?
6. Найдите объем прямоугольного параллелепипеда с ребрами 3 см, 5 см и 8 см.
а) 120 см3; б) 60 см3; в) 32 см3; г) другой ответ.
7. Длина прямоугольной комнаты в 2 раза больше ширины и на 2 м больше высоты. Найдите объем комнаты, если ее длина равна 6 м.
а) 432 м3; б) 144 м3; в) 72 м3; г) другой ответ.
8. Найдите объем куба, если площадь его развертки равна 96 см2.
а) 16 см3; б) 64 см3; в) 80 см3; г) другой ответ.
9. Найдите ребро куба, если его объем равен 512 м3.
а) 4 м; б) 8 м; в) 16 м; г) другой ответ.
10. Как изменится объем параллелепипеда, если его длину увеличить в 4 раза, ширину увеличить в 6 раз, а высоту уменьшить в 8 раз?
а) увеличится в 3 раза; б) уменьшится в 12 раз; в) не изменится; г) другой ответ.
 11. Три ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1; 0,5 и 16. Найдите ребро равновеликого ему куба.
11. Три ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1; 0,5 и 16. Найдите ребро равновеликого ему куба.
2 вариант
1. Выразите: а) в кубических дециметрах: 1 м3; 1 литр.
б) в кубических миллиметрах: 1 см3; 1 м3.
2.Ответьте «да» или «нет».
а) Р = 4а - периметр прямоугольника в) V = а 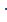 b
b 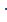 с - объём параллелепипеда
с - объём параллелепипеда
б) S = а·в - площадь квадрата
г) V = a3  объём куба
объём куба
3. Объём каждого маленького кубика 1 куб. ед. Найдите объём фигур, изображённых на рисунках.


4. Объём параллелепипеда равен 40 см3.Его размеры 2 см, 5см.Проставьте недостающий размер.
5  . а) б) Каковы измерения параллелепипеда на рис. б),
. а) б) Каковы измерения параллелепипеда на рис. б),
 сложенного из 3 одинаковых брусков,
сложенного из 3 одинаковых брусков,

 изображённых на рис. а). Каков его объём?
изображённых на рис. а). Каков его объём?
 1 см 8 см
1 см 8 см
2 см
6. Найдите объем прямоугольного параллелепипеда с ребрами 6 см, 3 см и 4 см.
а) 72 см3; б) 13 см3; в) 22 см3; г) другой ответ.
7. Длина прямоугольной комнаты в 3 раза больше ширины и на 2 м больше высоты. Найдите объем комнаты, если ее длина равна 6 м.
а) 432 м3; б) 144 м3; в) 48 м3; г) другой ответ.
8. Найдите объем куба, если площадь его развертки равна 150 см2.
а) 16 см3; б) 125 см3; в) 80 см3; г) другой ответ.
9. Найдите ребро куба, если его объем равен 729 м3.
а) 9 м; б) 8 м; в) 16 м; г) другой ответ.
10. Как изменится объем параллелепипеда, если его длину увеличить в 5 раза, ширину увеличить в 8 раз, а высоту уменьшить в 10 раз?
а) увеличится в 4 раза; б) уменьшится в 12 раз; в) не изменится; г) другой ответ.
 11. Площадь грани прямоугольного параллелепипеда равна 12. Ребро, перпендикулярное
11. Площадь грани прямоугольного параллелепипеда равна 12. Ребро, перпендикулярное
Практическое занятие №34
Решение задач на определение элементов пирамиды
Цели:
Образовательная: продолжить формирование у студентов умений решать задачи по теме «Пирамида».
Воспитательная: воспитание самостоятельности, творческого подхода к решению задач.
Развивающая: развитие логического мышления, навыков сравнительного анализа.
Оборудование: доска, компьютер, проектор, экран, индивидуальные карточки-задания, записи на доске.
План занятия.
Подготовительный этап.
Повторение опорных знаний.
1) Проверка усвоения пройденного материала фронтально (или индивидуально) по следующим вопросам (на экран проектируются вопросы, на которые студенты отвечают устно).
1. Дайте определение пирамиды.
2. Что называется диагональным сечением пирамиды?
3. Какая пирамида называется правильной?
4. На макете укажите все элементы пирамиды.
5. Сформулируйте теорему о свойстве параллельных сечений пирамиды.
Теоретический этап.
а) (Устно по готовому чертежу). Смоделируйте пирамиду, в основании которой лежит остроугольный треугольник, и обозначьте ее. Назовите:
1) вершины
2) ребра основания
3)боковые ребра
4) основание
5) боковые грани
6) высоту призмы
7)угол между боковым ребром и основанием
8) угол между боковой гранью и основанием
9)угол между высотой и боковой гранью
10) угол между высотой и боковым ребром
б) ДАВС- правильная пирамида. ДО перпендикулярно АВС. СК перпендикулярно АВ, АМ перпендикулярно ВС, ВN перпендикулярно АС, АВ= 6 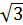 , ДО=4. Найдите sin <ДКО.
, ДО=4. Найдите sin <ДКО.
Практический этап.
Самостоятельное применение умений и знаний.
Провести самостоятельную работу в 15 вариантах. (Приложение 1)
Приложение 1
Варианты для самостоятельной работы.
Вариант 1.
Задача 1.
Смоделируйте пирамиду, в основании которой лежит треугольник, и обозначьте ее. Назовите:
1) вершины
2)ребра оснований
3) боковые ребра
4) основание
5) боковые грани
6) высоту пирамиды
7) апофему
8)угол между боковым ребром и основанием
9) угол между боковой гранью и основанием
10) угол между боковым ребром и высотой.
Задача 2.
ДАВС- правильная пирамида. ДО перпендикулярно АВС. СК перпендикулярно АВ, АМ перпендикулярно ВС, ВN перпендикулярно АС, АВ= 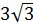 , АД=5. Найдите ДО.
, АД=5. Найдите ДО.
Задача 3.
Дано: ΔАВС, <АСВ=90°, ДО перпендикулярно (АВС), ДО =8, О- точка пересечения медиан, АД=10, АС= 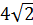 . Найдите ВС.
. Найдите ВС.
Вариант 2.
Задача 1.
Смоделируйте пирамиду, в основании которой лежит квадрат, и обозначьте ее. Назовите:
1) вершины
2)ребра оснований
3) боковые ребра
4) основание
5) боковые грани
6) высоту пирамиды
7) апофему
8)угол между боковым ребром и основанием
9) угол между боковой гранью и основанием
10) угол между боковым ребром и высотой.
Задача 2.
ДАВС- правильная пирамида. ДО перпендикулярно АВС. СК перпендикулярно АВ, АМ перпендикулярно ВС, ВN перпендикулярно АС. АД= 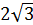 ,<АДВ= 120°. Найдите РОСН.
,<АДВ= 120°. Найдите РОСН.
Задача 3.
Дано: ΔАВС, <АСВ=90°, АС=СВ , ДО перпендикулярно (АВС), АД = 5, ДО = 3, О- точка пересечения медиан. Найдите S осн.
Вариант 3
Задача 1.
Смоделируйте пирамиду, в основании которой лежит остроугольный треугольник, и обозначьте ее. Назовите:
1) вершины
2)ребра оснований
3) боковые ребра
4) основание
5) боковые грани
6) высоту пирамиды
7) апофему
8)угол между боковым ребром и основанием
9) угол между боковой гранью и основанием
10) угол между боковым ребром и высотой.
Задача 2.
ДАВС- правильная пирамида. ДО перпендикулярно АВС. СК перпендикулярно АВ, АМ перпендикулярно ВС, ВN перпендикулярно АС. ВС=СД= 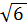 . Найдите ДО.
. Найдите ДО.
Задача 3.
Дано: ΔАВС, <АСВ=90°, ОєАВ, АО=ОВ=9, ДО перпендикулярно (АВС), Q-точка пересечения медиан, ДQ =5. Найдите ДО.
Вариант 4
Задача 1.
Смоделируйте пирамиду, в основании которой лежит ромб, и обозначьте ее. Назовите:
1) вершины
2)ребра оснований
3) боковые ребра
4) основание
5) боковые грани
6) высоту пирамиды
7) апофему
8)угол между боковым ребром и основанием
9) угол между боковой гранью и основанием
10) угол между боковым ребром и высотой.
Задача 2.
ДАВС- правильная пирамида. ДО перпендикулярно АВС. СК перпендикулярно АВ, АМ перпендикулярно ВС, ВN перпендикулярно АС. КР- биссектриса <ДКС, ДР:РС=2:3. Найдите <ДКС.
Задача 3.
Дано: ΔАВС, <АСВ=90°, Ас =3, ВС=4, ДО перпендикулярно (АВС), О-центр вписанной окружности, ДО= 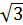 . Найдите расстояние от точки Д до прямой АС.
. Найдите расстояние от точки Д до прямой АС.
Вариант 5
Задача 1.
Смоделируйте пирамиду, в основании которой лежит тупоугольный треугольник, и обозначьте ее. Назовите:
1) вершины
2)ребра оснований
3) боковые ребра
4) основание
5) боковые грани
6) высоту пирамиды
7) апофему
8)угол между боковым ребром и основанием
9) угол между боковой гранью и основанием
10) угол между боковым ребром и высотой.
Задача 2.
ДАВС- правильная пирамида. ДО перпендикулярно АВС. СК перпендикулярно АВ, АМ перпендикулярно ВС, ВN перпендикулярно АС. АВ= 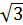 , tg<ДКС= 6. Найдите ДО.
, tg<ДКС= 6. Найдите ДО.
Задача 3.
Дано: ΔАВС, <АСВ=90°, АС =6, ВС=8, ДО перпендикулярно (АВС), ДО=3 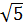 , О – центр вписанной окружности. Найти SΔАДС.
, О – центр вписанной окружности. Найти SΔАДС.
Вариант 6
Задача 1. Смоделируйте пирамиду, в основании которой лежит параллелограмм, и обозначьте ее. Назовите:
1) вершины
2)ребра оснований
3) боковые ребра
4) основание
5) боковые грани
6) высоту пирамиды
7) апофему
8)угол между боковым ребром и основанием
9) угол между боковой гранью и основанием
10) угол между боковым ребром и высотой.
Задача 2.
ДАВС- правильная пирамида. ДО перпендикулярно АВС. СК перпендикулярно АВ, АМ перпендикулярно ВС, ВN перпендикулярно АС, АВ=10 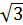 , cos <ДМО=0,2. Найдите апофему ДМ.
, cos <ДМО=0,2. Найдите апофему ДМ.
Задача 3.
Дано: ΔАВС, <АСВ=90°, АС =6, ВС=8, ДО перпендикулярно (АВС), ДО=3 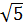 , О- центр вписанной окружности. Найти SΔАВД
, О- центр вписанной окружности. Найти SΔАВД
Практическое занятие № 35
Построение сечений многогранников плоскостями
Цели:
1. Проверить степень усвоения пройденного материала;
2. Развить логическое мышление;
3. Совершенствовать навыки решения задач по данной теме.
1 вариант
Построить сечение куба DKEFD1K1E1F1 плоскостью, проходящей через точки А, В, и С, данные на ребрах K1 E1, KE и D1K1.
2 вариант
Построить сечение четырехугольной пирамиды SABCD плоскостью, проходящей через три точки К, L, М, данные на ребрах SA, SB, SC пирамиды.
1 вариант
1. Построить сечение шестиугольной призмы плоскостью, заданной точками M, N и P на боковых гранях.
2. Построить сечение пятиугольной пирамиды, если плоскость проходит через т. M, принадлежащую боковому ребру, т. N, принадлежащую одной из граней пирамиды и т. P, лежащую на продолжении бокового ребра.
2 вариант
1. Построить сечение шестиугольной пирамиды плоскостью, заданной точками M, N и P на боковых не соседних гранях.
2. Построить сечение параллелепипеда, если плоскость проходит через т. M и N на боковых рёбрах и т. P на плоскости боковой грани, но не принадлежащей этой грани.
3 вариант
1. Построить сечение пятиугольной призмы плоскостью, заданной точками M, N и P на боковых не соседних рёбрах.
2. Построить сечение шестиугольной пирамиды, если плоскость проходит через т. M и N на двух различных боковых гранях и т. P на продолжении бокового ребра.
Математический диктант.
1. Что такое «произвольное параллельное проектирование»?
Любой плоский четырёхугольник ABCD вместе с его диагоналями может быть принят за параллельную проекцию тетраэдра, подобный тетраэдру A0B0C0D0 произвольной формы.
2. Какими свойствами должны обладать требования к построению сечений многогранников?
Верное изображение, наглядное.
3. Что называется оригиналом фигуры?
Считается любая фигура Ф подобная Ф0.
4. Как по-другому мы можем назвать параллельное проектирование?
Внутреннее вспомогательное.
5. Неполное изображение - это …?
Иллюстративные чертежи.
6. Перечислите основные построения?
Построения плоскости, проходящей через 3 точки; построение линии пересечения 2-х плоскостей; известные построения на плоскости.
7. Три метода построений сечения многогранников?
Метод следов, метод вспомогательных сечений, комбинированный метод.
8. Как по-другому называется метод вспомогательных сечений?
Внутреннее проектирование.
9. Как по-другому называется комбинированный метод?
Ортогональная проекция.
ЕГЭ
Дан куб ABCDA´B´C´D´, где АА´, ВВ´, СС´, DD´ - боковые ребра. Построить сечение куба плоскостью, проходящей через вершину А и середины ребер В´С´ и С´D´
 Решение:
Решение:
1. KL∩A´B´=F
KL∩D´C´=E
2. AE∩DD´=N
3. AF∩BB´=M
4. NKLMA – искомое сечение
Исторический экскурс
Построения сечения многогранников
Наиболее доступными и эффективными в практике преподавания геометрии в средней школе являются следующие три метода построения сечений многогранников:
1. Метод следов.
2. Метод вспомогательных сечений.
3. Комбинированный метод.
Метод следов.
В общем случае секущая плоскость пересекает плоскость каждой грани многогранника и каждую из прямых, на которых лежат ребра многогранника. Прямую, по которой секущая плоскость пересекает плоскость какой-либо грани многогранника, называют следом секущей плоскости на плоскости этой грани, а точку, в которой секущая плоскость пересекает прямую, содержащую какое-нибудь ребро, называют следом секущей плоскости на этой прямой. Если секущая плоскость пересекает непосредственно грань многогранника, то можно также говорить о следе секущей плоскости на грани и аналогично говорить о следе на ребре.
След секущей плоскости на плоскости нижнего основания условимся ради краткости речи называть просто следом секущей плоскости. С построения именно этого следа чаще всего начинают построение сечения многогранника.
Способы задания сечения весьма разнообразны. Наиболее распространенным из них является способ задания секущей плоскости тремя точками, не лежащими на одной прямой.
В тех случаях, когда сечение строится с помощью следа на плоскости нижнего основания, задавая три точки, принадлежащие непосредственно секущей плоскости, следует указать их таким образом, чтобы проекции этих точек на плоскость нижнего основания (вторичные проекции) строились однозначно. Сделать это можно, например, если указать, на каком ребре лежит заданная точка или в какой грани и т. д.
При этом если многогранником, сечение которого строится, является призма, то проектирование (внутреннее) на, плоскость нижнего основания выполняется параллельное. Его направление определяется боковым ребром призмы. Если же многогранником является пирамида, то выполняется центральное (внутреннее) проектирование на плоскость основания. Центром проектирования является вершина пирамиды, в которой сходятся все боковые ребра.
Метод вспомогательных сечений.
Этот метод в достаточной мере является универсальным и имеет определенные преимущества по сравнению с методом следов в тех случаях, когда нужный след секущей плоскости оказывается за пределами чертежа. Вместе с тем построения при использовании этого метода получаются «скученными», так как все они выполняются внутри многогранника (это обстоятельство послужило причиной называть рассматриваемый метод также методом внутреннего проектирования).
Комбинированный метод.
Суть этого метода состоит в применении теорем о параллельности прямых и плоскостей в сочетании с методом следов, или с методом вспомогательных сечений, или с обоими этими методами.
Кроссворд.
По горизонтали:
1.Тело, ограниченное конической поверхностью и кругом с границей L.
2. Поверхность, простирающаяся неограниченно во все стороны.
3. Поверхность, составленная из двух равных параллелограммов ABCD и A1B1C1D1 и четырех параллелограммов.
4. Метод, суть которого состоит в том, что искомая величина находится с помощью уравнения, составленного по условию задачи.
5. Тело, ограниченное цилиндрической поверхностью и двумя кругами L1 и L2.
6. Тело, ограниченное сферой.
По вертикали:
3. Многогранник, составленный из n-угольника А1А2...Аn и n треугольников.
7. Метод, который чаще всего используется при решении задач на доказательство.
8. Прямоугольный параллелепипед, у которого все три измерения равны.
9. Многогранник, составленный из двух равных многоугольников А1А2...Аn и В1В2...Вn , расположенных в параллельных плоскостях, и n параллелограммов.


Занимательные задачи
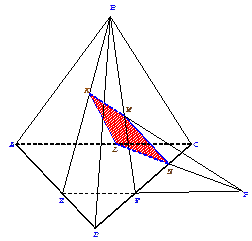
Боковое ребро правильной треугольной пирамиды вдвое больше стороны основания. Как построить сечение, которое проходит через сторону основания перпендикулярно скрещивающемуся с этой стороной боковому ребру?
Дано: MABC- правильная
треугольная пирамида, BM=2AB.
Построить: сечение ADB.
Решение: 
Анализ.
Поиск решения задачи проведем, полагая задачу решенной. Сечение ADB проходит через сторону AB перпендикулярно стороне MC. Если MC перпендикулярно ADB, то MC перпендикулярно BD и AD. K – середина MC, ∆KBC – равнобедренный, его медиана CP является и высотой, высота KE параллельно MO. Через точку пересечения CP и KE проходит третья высота BD.
Построение.
1.MK=KC; 2.KE 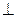 BC; 3.MO| |KE; 4.через CP∩KE проводим высоту BD; 5.ADB – искомое сечение.
BC; 3.MO| |KE; 4.через CP∩KE проводим высоту BD; 5.ADB – искомое сечение.
Доказательство.
Построенное сечение удовлетворяет всем условиям задачи.
Исследование.
2-ое решение: если ABD - искомое сечение, то BD 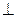 MC, MO
MC, MO 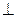 BC, треугольники BCD и MCO подобны: BC:MC=DC:OC,
BC, треугольники BCD и MCO подобны: BC:MC=DC:OC, 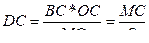 .
.
Наглядность.
Метод следов.

Метод вспомогательных сечений.
Комбинированный метод.

Практическое занятие № 36
Решение задач на нахождение элементов цилиндра и конуса
Цели:
Обучающие:
• Формировать умения применять понятия цилиндра, конуса и формулы для вычисления площади боковой поверхности при решении задач в контексте ЕГЭ.
Развивающие:
• Способствовать развитию умений учащихся обобщать полученные знания, проводить анализ синтез, сравнения, делать необходимые выводы при решении задач разного уровня сложности.
• Способствовать развитию умений творческого подхода к решению практических задач.
1. Осевое сечение цилиндра – квадрат со стороной 6 см. Найти высоту и радиус основания цилиндра.
2. Высота конуса 4 см, радиус основания – 3 см. Найти образующую конуса.
3. Высота конуса 12 см, образующая – 13 см. Найти боковую поверхность конуса.
4. Радиус основания цилиндра равен 2м, высота 3м. Найти диагональ осевого сечения.
5. Осевое сечение конуса равносторонний треугольник со стороной 10см. Найти радиус основания и высоту конуса.
6. Длина окружности основания цилиндра равна 1. Площадь боковой поверхности равна 2. Найдите высоту цилиндра.
7. Радиус основания конуса равен 3, высота равна 4. Найдите площадь полной поверхности конуса, деленную на π. 1
8. Образующая конуса равна 10, высота конуса 6. Найдите радиус конуса.2
9. Осевое сечение конуса равносторонний треугольник со стороной 10см. Найти площадь боковой поверхности конуса.3
10. Диагональ осевого сечения цилиндра равна 48. Угол между этой диагональю и образующей равен 300. Найдите радиус цилиндра.2
11. Во сколько раз увеличится площадь боковой поверхности конуса, если его образующую увеличить в 3 раза?1
12. Осевое сечение конуса равносторонний треугольник со стороной 10см. Найти радиус основания и высоту конуса.2
13. Радиус основания цилиндра равен 6, высота равна 3. Найдите площадь боковой поверхности цилиндра, деленную на π. 1
14. Высота конуса 12 см, образующая – 13 см. Найти боковую поверхность конуса.3
15. Длина окружности основания цилиндра равна 1. Площадь боковой поверхности равна 2. Найдите высоту цилиндра.
16. Осевое сечение конуса равносторонний треугольник со стороной 10см. Найти радиус основания и высоту конуса.
17. Диагональ осевого сечения цилиндра наклонена к плоскости основания под углом 60° и равна 20 см. Найдите площадь боковой поверхности цилиндра.
18. Высота конуса равна 2 √3 см. Найдите площадь боковой поверхности и площадь осевого сечения конуса, если оно является правильным треугольником.
19. Диаметр окружности основания цилиндра равен 26, а его образующая – 21. Плоскость пересекает его основания по хордам длины 24 и 10. Найти угол между этой плоскостью и плоскостью основания цилиндра.
Практическое занятие № 37
Определение площади сферы, объема шара
Цели:
образовательные:
· обобщить и систематизировать знания обучающихся по теме «Тела вращения»; вывести формулу объема шара и площади сферы.
воспитательные:
· показать, что источник возникновения изучаемой темы – реальный мир, что она возникла из практических потребностей; воспитание вычислительных навыков;
· показать связь с историей; воспитание самостоятельности; воспитание стремления к самореализации.
развивающие:
· совершенствование, развитие, углубление знаний, умений и навыков по теме; развитие пространственного воображения; развитие мыслительной деятельности: умения анализировать, обобщать, классифицировать.
Соотнесите название фигуры и формулу объема и площади поверхности тел.1.Цилиндр. 2.Конус. 3.Усеченный конус. 4. Шар.
V=1/3SОСНH=1/3∏R2H V=SОСНH=πR2H V=1/3∏H(R2+r2+Rr) S=4 πR2
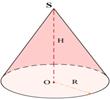
Шаром называется множество всех точек пространства, находящихся от данной точки на расстоянии, не больше данного R.
Радиусом шара называют всякий отрезок, соединяющий центр шара с точкой шаровой поверхности.
Отрезок, соединяющий две точки шаровой поверхности и проходящий через центр шара, называется диаметром шара.
Концы любого диаметра шара называются диаметрально противоположными точками шара. Отрезок, соединяющий две любые точки шаровой поверхности и не являющийся диаметром шара, называют хордой шара.
Теорема: Объем шара равен 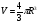
Доказательство:
Мы уже знаем, что можно вычислять объёмы тел с помощью интегральной формулы
V= 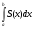
Давайте посмотрим, как это можно сделать для вывода формулы объема шара.
(Учитель объясняет вывод формулы объёма шара с помощью формулы, ученики делают записи в тетрадях).
Рассмотрим шар радиуса R с центром в точке О и выберем ось ОХ произвольным образом (рис192).Сечение шара плоскостью, перпендикулярной к оси ОХ и проходящий через точку М этой оси, является кругом с центом в точке М. Обозначим радиус этого круга через r, а его площадь через S(х), где х абсцисса точки М. Выразим S(х) через х и R. Из прямоугольного треугольника ОМС находим 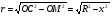 . Тогда
. Тогда 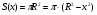 , где
, где 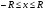
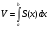
Так как 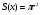 , то заменяя r через выражение
, то заменяя r через выражение 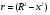 получим
получим 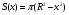
Заметим, что эта формула верна для любого положения точки М на диаметре АВ, т.е. для всех х, удовлетворяющих условию 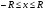
Применяя основную формулу для вычисления объемов тел при а= -R, b=R, получим
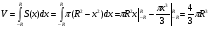
Теорема доказана.
В практических приложениях часто указывается диаметр шара, поэтому в процессе решения задач полезно знать формулу 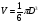 , где D – диаметр шара
, где D – диаметр шара
ПРОБЛЕМНАЯ ЗАДАЧА: При уличной торговле арбузами весы отсутствовали. Однако выход был найден: арбуз диаметром 3 дм приравнивали по стоимости к трём арбузам диаметром 1 дм.
Что вы возьмете? Правы ли были продавцы
Решение:
Необходимо найти объемы данных арбузов.
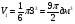
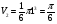 и таких арбузов три, значит их общий объем равен
и таких арбузов три, значит их общий объем равен 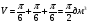
Задача (Архимеда): На надгробном камне могилы Архимеда в Сиракузах изображен цилиндр с вписанным в него шаром. Это символ открытия формул объема шара и площади сферы, а также важного вывода, что «объем шара, вписанного в цилиндр в …раз меньше объема цилиндра и что также относятся площади поверхностей этих тел». Найдите отношение объема цилиндра к объему шара и отношение площади поверхности цилиндра к площади поверхности шара.
Дано: в цилиндр вписан шар
Найти: отношение объёмов цилиндра и шара, отношение площадей поверхностей
РЕШЕНИЕ:
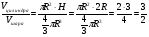
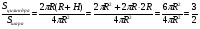
Ответ:1,5
Одним из своих наивысших достижений Архимед считал доказательство того, что объём шара в полтора раза меньше объёма описанного около него цилиндра. Недаром шар, вписанный в цилиндр, был высечен на надгробии Архимеда в Сиракузах.
ПРАКТИЧЕСКАЯ РАБОТА «Вычисление объёмов тел вращения»
Задачи :
1.Около шара описан цилиндр, площадь поверхности
которого равна 18. Найдите площадь поверхности шара.
Решение: (Опираемся на открытие Архимеда)
Ответ: 12
2.Площадь поверхности шара уменьшили 9 раз. Во сколько раз уменьшился объем шара?
Решение:
Пусть радиус первого шара R, а уменьшенного r.
Поверхность шара S1 = 4пR2, стала S2 = 4пR2/9 = 4п (R/3)2 = 4пr2
Видим, что r = 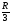 , т.е. радиус уменьшился в 3 раза.
, т.е. радиус уменьшился в 3 раза.
Объем V1= 4/3 ПR3, а объем V2= 4/3 пr3 = 4/3 п(R/3)3 =4/3 пR3 /27 = V1 / 27.
Ответ:27
Практическое занятие №38
Выполнение действий на нахождение производных
Цель работы: научиться вычислять производные различных функций, пользуясь правилами дифференцирования и таблицей производных
Задачи для решения на практической работе
ВАРИАНТ 1
Задание 1. Вычислить производные данных функций, пользуясь таблицей производных и соответствующими правилами дифференцирования:
ПРИМЕРЫ: Воспользуемся правилом нахождения производной суммы-разности функций, правилом вынесения постоянного множителя за знак производной и формулой 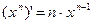 . Помним, что производная постоянного равна нулю!
. Помним, что производная постоянного равна нулю!
а) 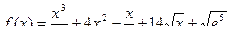 , найти
, найти 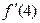 :
:
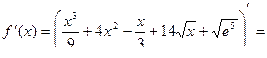
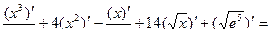
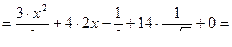
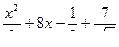 ;
; 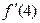
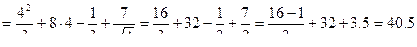
б) 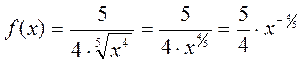 , найти
, найти 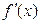 :
:
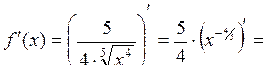
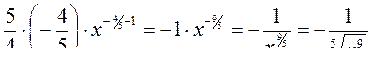 .
.
в,г,д) 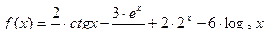 , найти
, найти 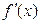 :
:
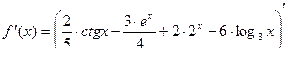
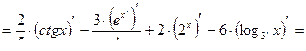
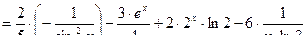
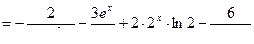 .
.
РЕШИТЕ САМОСТОЯТЕЛЬНО:
а) 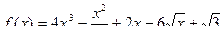 , найти
, найти 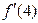 ; б)
; б) 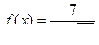 , найти
, найти 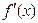 ;
;
в) 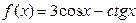 , найти
, найти 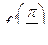 ; г)
; г) 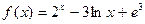 , найти
, найти 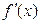 ;
;
д) 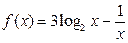 , найти
, найти 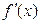 .
.
Задание 2. Вычислить производные данных функций, пользуясь соответствующими правилами дифференцирования:
ПРИМЕРЫ: а) 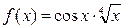 , найти
, найти 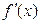 :
:
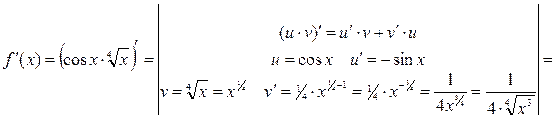

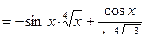 .
.
б) 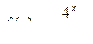 , найти
, найти 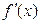 :
:
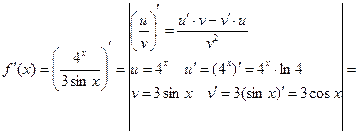
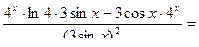
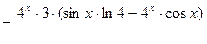
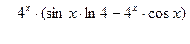 .
.
РЕШИТЕ САМОСТОЯТЕЛЬНО:
а) 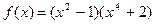 , найти
, найти 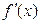 ; б)
; б) 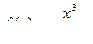 ,найти
,найти 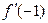 ;
;
в) 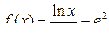 , найти
, найти 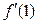 ; г)
; г) 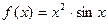 , найти
, найти 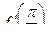 .
.
Задание 3. Решить уравнение: 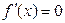 , если
, если 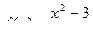 .
.
ПРИМЕР: Решить уравнение: 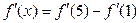 , если
, если 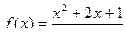 .
.
Решение:
1) 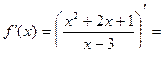
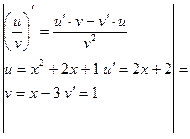
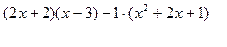
= 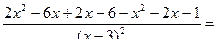
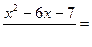
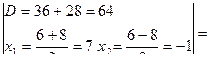
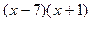 .
.
2) 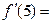
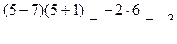 ,
, 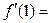
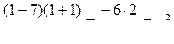 ,
, 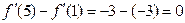 ,
,
3) Имеем уравнение: 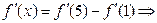
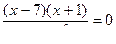
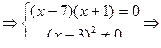
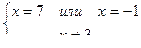 . Ответ: -1 или 7.
. Ответ: -1 или 7.
Задание 4. Решить неравенство: 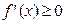 , если
, если 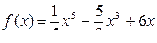 .
.
ПРИМЕР. Решить неравенство: 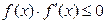 , если
, если 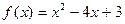 .
.
Решение: 1) 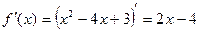 .
.
2) Имеем неравенство: 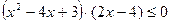 . Неравенство степени больше второй решается методом интервалов.
. Неравенство степени больше второй решается методом интервалов.
Пусть 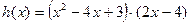 . Нули функции:
. Нули функции: 
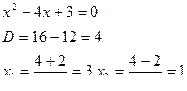 или
или 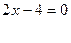
Отметим найденные значения на оси Ох и определим знаки на полученных интервалах:
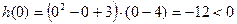

Корни не повторяются – знаки чередуются.
Ответ: 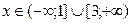
Задание 5. Найти 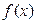 , если известна её производная
, если известна её производная 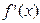 :
: 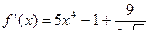 .
.
ПРИМЕР. Найти 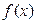 , если известна её производная
, если известна её производная 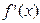 :
:  .
.
Решение: определим производной какого выражения является каждое слагаемое функции:
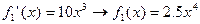 ,
, 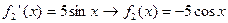 ,
, 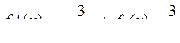 .
.
Значит, 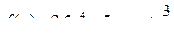 .
.
Задание 6.* 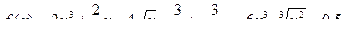 . Найти
. Найти 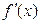 .
.
СДЕЛАТЬ ВЫВОД К ДАННОЙ РАБОТЕ, ОТВЕТИВ НА ВОПРОСЫ:
1) Запишите определение производной;
2) Как называется операция нахождения производной?
3) Запишите формулы производной произведения и частного;
4) Найдите производные следующих функций: 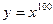 ,
, 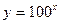 ,
, 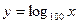 ;
;
5) Производная какой функции равна 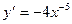 ?
?
Замечания по выполнению практической работы:
1) Работа состоит из 6 заданий, выполняется на оценку «3», «4» или «5», по окончании работы необходимо сделать вывод и побеседовать о выполненной работе с преподавателем.
2) Критерий оценки:
на оценку «3» необходимо выполнить задания №1, №2 и №3 или №4 без грубых ошибок, на оценку «4» - верно выполнить пять заданий, на оценку «5» - выполнить все задания.
3) Для выполнения работы необходимо повторить правила дифференцирования, таблицу производных основных элементарных функций.
4) При возникновении трудностей при решении заданий, необходимо обратиться к лекциям, методическим указаниям, преподавателю.
ВАРИАНТ 2
Задание 1. Вычислить производные данных функций, пользуясь таблицей производных и соответствующими правилами дифференцирования:
ПРИМЕРЫ: Воспользуемся правилом нахождения производной суммы-разности функций, правилом вынесения постоянного множителя за знак производной и формулой 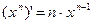 . Помним, что производная постоянного равна нулю!
. Помним, что производная постоянного равна нулю!
а) 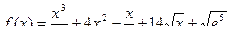 , найти
, найти 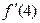 :
:
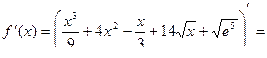
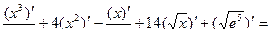
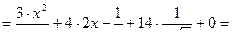
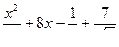 ;
; 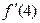
б) 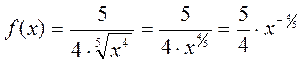 , найти
, найти 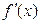 :
:
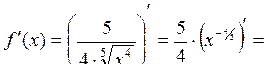
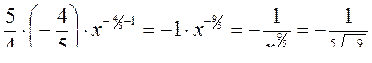 .
.
в,г,д) 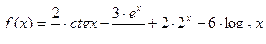 , найти
, найти 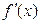 :
:
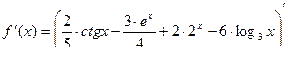
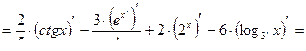
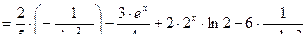
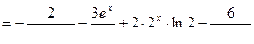 .
.
РЕШИТЕ САМОСТОЯТЕЛЬНО:
а) 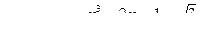 , найти
, найти 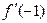 ; б)
; б) 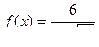 , найти
, найти 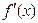 ;
;
в) 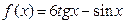 , найти
, найти 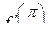 ; г)
; г) 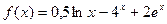 , найти
, найти 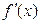 ;
;
д) 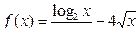 , найти
, найти 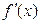 .
.
Задание 2. Вычислить производные данных функций, пользуясь соответствующими правилами дифференцирования:
ПРИМЕРЫ: а) 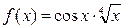 , найти
, найти 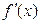 :
:
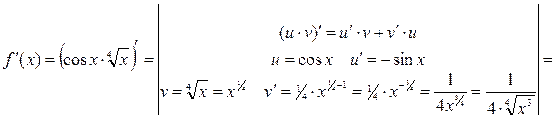

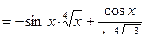 .
.
б) 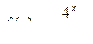 , найти
, найти 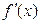 :
:
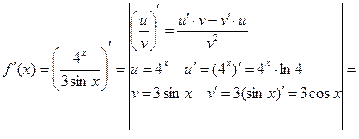
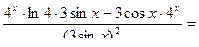
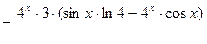
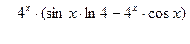 .
.
РЕШИТЕ САМОСТОЯТЕЛЬНО:
а) 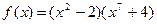 , найти
, найти 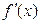 ; б)
; б) 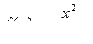 ,найти
,найти 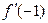 ;
;
в) 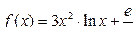 , найти
, найти 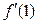 ; г)
; г) 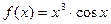 , найти
, найти 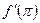 .
.
Задание 3. Решить уравнение: 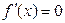 , если
, если 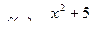 .
.
ПРИМЕР: Решить уравнение: 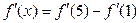 , если
, если 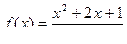 .
.
Решение:
1) 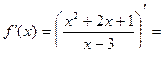
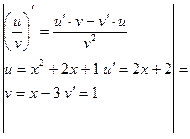
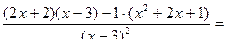
= 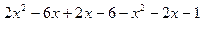
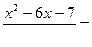
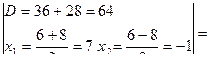
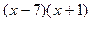 .
.
2) 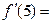
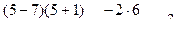 ,
, 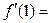
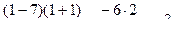 ,
, 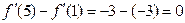 ,
,
3) Имеем уравнение: 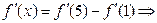
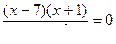
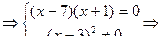
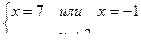 . Ответ: -1 или 7.
. Ответ: -1 или 7.
Задание 4. Решить неравенство: 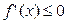 , если
, если 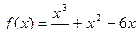 .
.
ПРИМЕР. Решить неравенство: 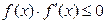 , если
, если 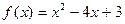 .
.
Решение: 1) 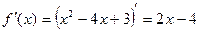 .
.
2) Имеем неравенство: 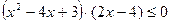 . Неравенство степени больше второй решается методом интервалов.
. Неравенство степени больше второй решается методом интервалов.
Пусть 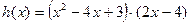 . Нули функции:
. Нули функции: 
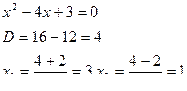 или
или 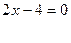
Отметим найденные значения на оси Ох и определим знаки на полученных интервалах:

Корни не повторяются – знаки чередуются.
Ответ: 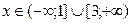
Задание 5. Найти 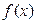 , если известна её производная
, если известна её производная 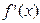 :
: 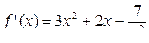 .
.
ПРИМЕР. Найти 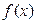 , если известна её производная
, если известна её производная 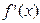 :
:  .
.
Решение: определим производной какого выражения является каждое слагаемое функции:
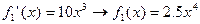 ,
, 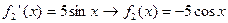 ,
, 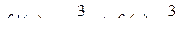 .
.
Значит, 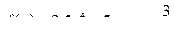 .
.
Задание 6.* 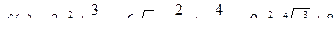 . Найти
. Найти 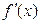 .
.
СДЕЛАТЬ ВЫВОД К ДАННОЙ РАБОТЕ, ОТВЕТИВ НА ВОПРОСЫ:
1) Запишите определение производной;
2) Как называется операция нахождения производной?
3) Запишите формулы производной произведения и частного;
4) Найдите производные следующих функций: 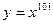 ,
, 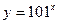 ,
, 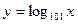 ;
;
5) Производная какой функции равна 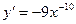 ?
?
Практическое занятие № 39
Выполнение заданий на применение производной к исследованию функций
Цели выполнения работы:
- Исследовать правило применения производной к исследованию функций на промежутки монотонности и экстремумы
- Применить данное правило при исследовании конкретных функций
- Осознать себя в данной теме
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ:
- Входной контроль: Исследование основных понятий
Дата: 2018-12-21, просмотров: 1367.