Пример №6. Возвести в степень комплексные числа 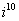 ,
, 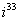 ,
, 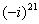
Если мнимая единица возводится в четную степень, то техника решения такова:
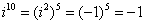
Если мнимая единица возводится в нечетную степень, то «отщипываем» одно «и», получая четную степень:
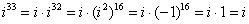
Если есть минус (или любой действительный коэффициент), то его необходимо предварительно отделить:

Извлечение корней из комплексных чисел. Квадратное уравнение с комплексными корнями
Пример №7. 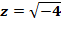
В комплексных числах извлечь корень – можно! А точнее, два корня:
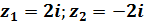
Такие корни также называют сопряженными комплексными корнями.
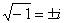 ,
, 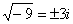 ,
, 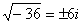 ,
, 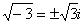 ,
, 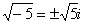 и т.д.
и т.д.
Во всех случаях получается два сопряженных комплексных корня.
Пример 8. Решить квадратное уравнение 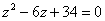
Вычислим дискриминант:
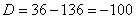
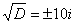
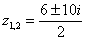
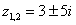 – сопряженные комплексные корни
– сопряженные комплексные корни
Порядок выполнения работы.
1. Внимательно изучите теоретическую справку по теме и рассмотрите примеры решения некоторых заданий.
2. Выполните самостоятельную работу по образцу.
| Задание 1. Даны два комплексных числа б) | |||
| 1 вариант | 2 вариант | ||
| 1 | 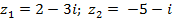
| 1 | 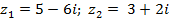
|
| 2 | 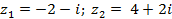
| 2 | 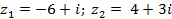
|
| 3 | 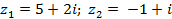
| 3 | 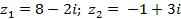
|
| 4 | 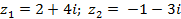
| 4 | 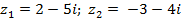
|
| 5 | 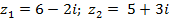
| 5 | 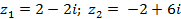
|
| 6 | 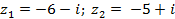
| 6 | 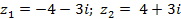
|
| 7* | 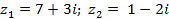
| 7* | 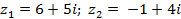
|
| 8* | 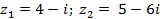
| 8* | 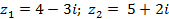
|
| 9* | 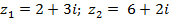
| 9* | 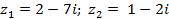
|
| 10* | 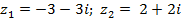
| 10* | 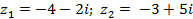
|
Обязательно к выполнению 6 вариантов комплексных чисел. Варианты 7-10 на дополнительную оценку.
Практическое занятие №3
Выполнение действий с арифметическим квадратным корнем
Цель: обобщить и систематизировать теоретический материал, закрепить практические навыки по теме «Квадратные корни»
Задачи
Образовательные:
· повторить и закрепить определение и свойства арифметического квадратного корня, правила вынесения множителя из-под знака корня и внесения множителя под знак корня;
· закрепить умение выполнять действия с арифметическими квадратными корнями, используя теоретический материал.
Развивающие:
· развивать познавательную активность, самостоятельность, сознательное восприятие учебного материала, вычислительные навыки.
Упражнения с решениями
1 Упростить выражения:
1) 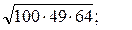 2)
2) 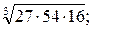 3)
3) 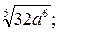
Образец решения:
1) Перемножать подкоренное выражение нет смысла, так как каждый из сомножителей представляет квадрат целого числа. Воспользуемся свойством 2:
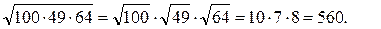
2) Попытаемся, если это возможно, представить подкоренное выражение в виде произведения множителей, каждый из которых является кубом целого числа, и применим свойство 2:
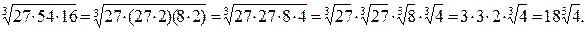
3) 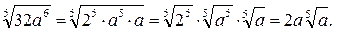
Решить и сверить ответ:
А 1) 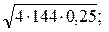 2)
2) 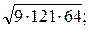 3)
3) 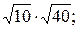 4)
4) 
Б 1) 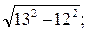 2)
2) 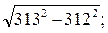 3)
3) 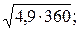 4)
4) 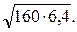
Ответы: А 1) 12; 2) 264; 3) 20; 4) 48.
Б 1) 5; 2) 25; 3) 42; 4) 32.
2 Найти значение выражения:
1) 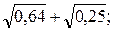 2)
2) 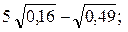 3)
3) 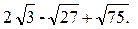
Образец решения:
1) В данном выражении первым действием является извлечение квадратного корня из числа. Вторым действием - сложение полученных результатов.
При вычислении используем 1-ое свойство корней:
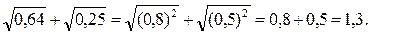
2) Аналогично предыдущему примеру, первым действием является извлечение квадратного корня из числа. Вторым и третьим действиями - умножение и разность полученных результатов.
При вычислении используем 1-ое свойство корней:
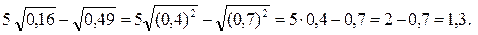
3) Преобразуем подкоренные выражения, извлечем корень, а затем упростим полученное выражение:
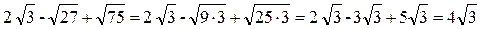 .
.
Решить и сверить ответ:
А 1) 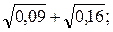 2)
2) 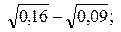 3)
3) 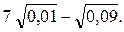
Б 1) 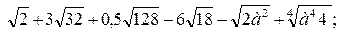
2) 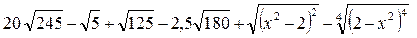
Ответы: А 1) 0,7; 2) 0,1; 3) 0,4.
Б 1) 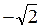 ; 2)
; 2) 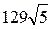 .
.
3 Возвести в степень:
1) 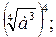 2)
2) 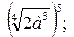 3)
3) 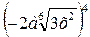 ; 4)
; 4) 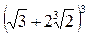
Образец решения:
При возведении корня в степень показатель корня остается без изменения, а показатели подкоренного выражения умножаются на показатель степени.
1) 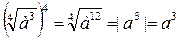 (так как
(так как 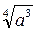 определен, то
определен, то 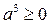 );
);
2) 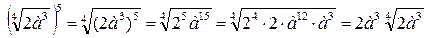 Если данный корень имеет коэффициент, то этот коэффициент возводится в степень отдельно и результат записывается коэффициентом при корне.
Если данный корень имеет коэффициент, то этот коэффициент возводится в степень отдельно и результат записывается коэффициентом при корне.
3) 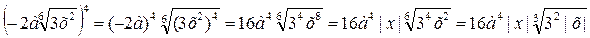
Здесь мы использовали свойство 6.
4) Выражение в скобках, представляющее сумму двух различных радикалов, возведем в куб и упростим: т 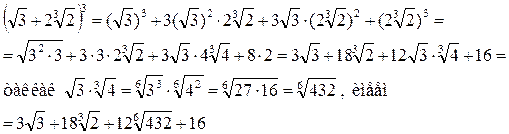
Дата: 2018-12-21, просмотров: 650.
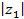 и
и 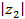 . Вычислите:
. Вычислите: 
