А 1) 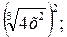 2)
2) 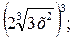 3)
3) 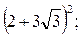 4)
4) 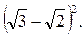
Б 1) 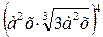 ; 2)
; 2) 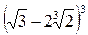 ; 3)
; 3) 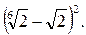
В 1) 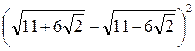 .
.
Ответы: А 1) 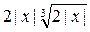 ; 2)
; 2) 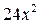 ; 3)
; 3) 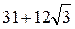 ; 4)
; 4) 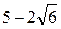 .
.
Б 1) 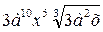 ; 2)
; 2) 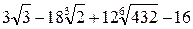 ; 3)
; 3) 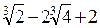 .
.
В 1) 8.
5 Исключите иррациональность в знаменателе:
1) 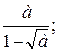 2)
2) 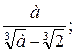 3)
3) 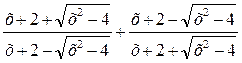 .
.
Образец решения:
Для исключения иррациональности в знаменателе дроби нужно подыскать простейшее из выражений, которое в произведении со знаменателем дает рациональное выражение, и умножить на подысканный множитель числитель и знаменатель данной дроби.
В более сложных случаях уничтожают иррациональность не сразу, а в несколько приемов.
1) В выражении 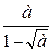 должно быть
должно быть 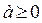 и
и 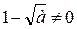 .
.
Умножая числитель и знаменатель дроби на 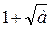 , получим:
, получим: 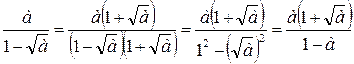 .
.
2) Умножая числитель и знаменатель дроби на неполный квадрат суммы, получим:
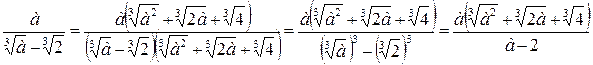
3) Приведем дроби к общему знаменателю: 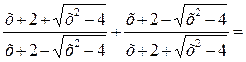
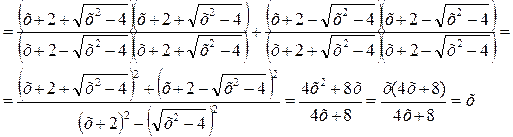
Решая данный пример, мы должны иметь в виду, что каждая дробь имеет смысл, т.е. знаменатель каждой дроби отличен от нуля. Кроме того, 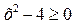 .
.
Проверь себя (решить и сверить ответ)
А 1) 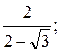 2)
2) 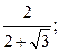 3)
3) 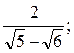 4)
4) 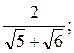 5)
5) 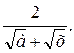
Б 1) 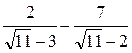 ; 2)
; 2) 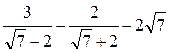 ; 3)
; 3) 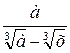 ;
;
4) 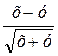 ; 5)
; 5) 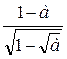 ; 6)
; 6) 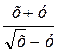 .
.
В 1) 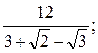 2)
2)  3)
3) 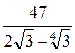 .
.
Ответы: А 1) 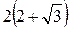 ; 2)
; 2)  ; 3)
; 3) 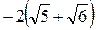 ; 4)
; 4) 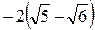 ; 5)
; 5) 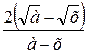 . Б 1) 1; 2)
. Б 1) 1; 2) 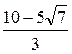 ; 3)
; 3) 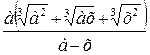 ; 4)
; 4) 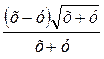 ; 5)
; 5) 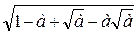 ; 6)
; 6) 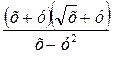 . В 1)
. В 1) 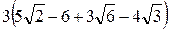 ; 2)
; 2) 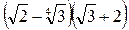 ; 3)
; 3) 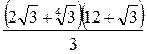 .
.
7 Найдите значение выражения:
1) 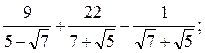
2) 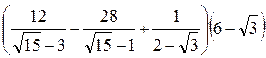 ;
;
3) 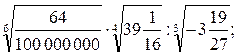
4) 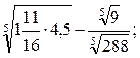
5) 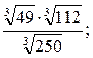
6)  .
.
Ответы: 1) 6; 2) 33; 3) -0,15; 4) 1; 5) 2,8; 6) 0,5.
Практическое занятие № 4
Выполнение преобразований с корнями n – ой степени
Цель работы:
Выполнить действия по преобразованию алгебраических, рациональных, иррациональных, степенных выражений.
КОРНИ НАТУРАЛЬНОЙ СТЕПЕНИ ИЗ ЧИСЛА, ИХ СВОЙСТВА
Корень n – степени: 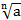 , n - показатель корня, а – подкоренное выражение
, n - показатель корня, а – подкоренное выражение
Если n – нечетное число, то выражение 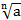 имеет смысл при
имеет смысл при 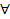 а
а
Если n – четное число, то выражение 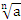 имеет смысл при
имеет смысл при 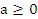
Арифметический корень: 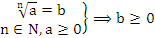
Корень нечетной степени из отрицательного числа: 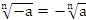
ОСНОВНЫЕ СВОЙСТВА КОРНЕЙ
1. Правило извлечения корня из произведения:
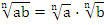
2. Правило извлечения корня из дроби:
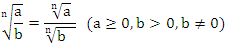
3. Правило извлечения корня из корня:
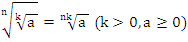
4. Правило вынесения множителя из под знака корня:
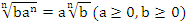
5. Внесение множителя под знак корня:
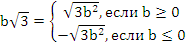 ,
,
6. Показатель корня и показатель подкоренного выражения можно умножить на одно и тоже число.

7. Правило возведения корня в степень.
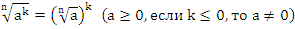
СТЕПЕНЬ С НАТУРАЛЬНЫМ ПОКАЗАТЕЛЕМ
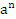 =
= 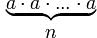 ,a – основание степени, n – показатель степени
,a – основание степени, n – показатель степени
Свойства:
1. При умножении степеней с одинаковыми основаниями показатели складываются, а основание остается неизменным.
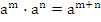
2. При делении степеней с одинаковыми основаниями показатели вычитаются, а основание остается неизменным.
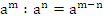
3. При возведении степени в степень показатели перемножаются.
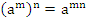
4. При возведении в степень произведения двух чисел, каждое число возводят в эту степень, а результаты перемножают.
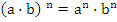
5. Если в степень возводят частное двух чисел, то в эту степень возводят числитель и знаменатель, а результат делят друг на друга.
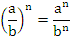
6. Если 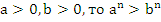
СТЕПЕНЬ С ЦЕЛЫМ ПОКАЗАТЕЛЕМ
1. 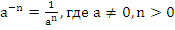
2. 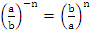
3. 
4. По определению: 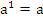
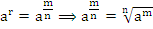
Свойства:
1. 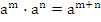
2. 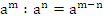
3. 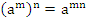
4. 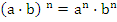
5. 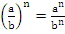
6. Пусть r рациональное число 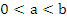 , тогда
, тогда
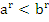 при r>0
при r>0 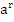 >
> 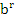 при r<0
при r<0
7 .Для любого рациональных чисел r и s из неравенства 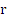 >
> 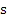 следует
следует
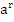 >
> 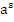 при a>1
при a>1 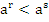 при
при 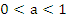
Формулы сокращённого умножения.
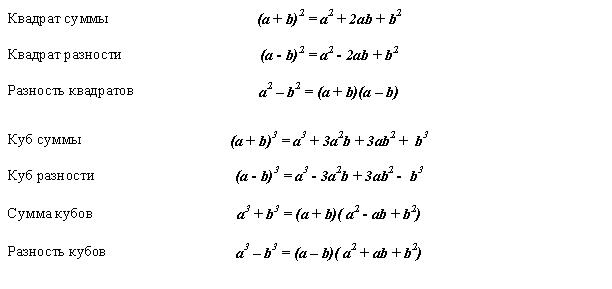
Пример 1. Упростите выражение 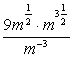 .
.
Решение
Применим свойства степеней (умножение степеней с одинаковым основанием и деление степеней с одинаковым основанием): 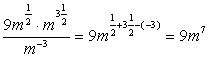 .
.
Ответ: 9m7 .
Пример 2.Сократить дробь: 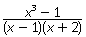
Решение. Так область определения дроби 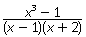 все числа, кроме х ≠ 1 и х ≠ -2.Вместе с тем
все числа, кроме х ≠ 1 и х ≠ -2.Вместе с тем 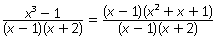 .Сократив дробь, получим
.Сократив дробь, получим 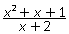 Область определения полученной дроби: х ≠ -2, т.е. шире, чем область определения первоначальной дроби. Поэтому дроби
Область определения полученной дроби: х ≠ -2, т.е. шире, чем область определения первоначальной дроби. Поэтому дроби 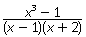 и
и 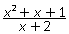 равны при х ≠ 1 и х ≠ -2.
равны при х ≠ 1 и х ≠ -2.
Пример 3.Сократить дробь: 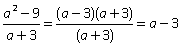
Пример 4.Упростить: 
Пример 5.Упростить: 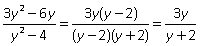
Пример 6. Упростить: 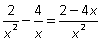
Пример 7. Упростить: 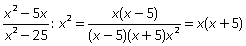
Пример 8.Упростить: 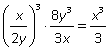
Пример 9. Вычислить: 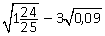 .
.
Решение. 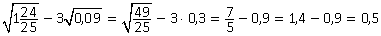
Пример 10.Упростить выражение: 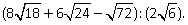
Решение. 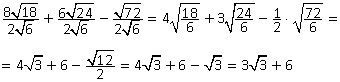
Пример 11.Сократить дробь 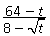 , если
, если 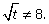
Решение. 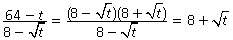 .
.
Пример 12.Освободиться от иррациональности в знаменателе дроби 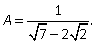
Решение. В знаменателе имеем иррациональность 2-й степени, поэтому помножим и числитель, и знаменатель дроби на сопряженное выражение, то есть сумму чисел 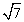 и
и 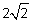 , тогда в знаменателе будем иметь разность квадратов, которая и ликвидирует иррациональность.
, тогда в знаменателе будем иметь разность квадратов, которая и ликвидирует иррациональность. 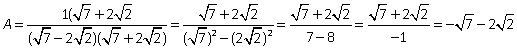
ВАРИАНТ - I
1. Упростите выражение:
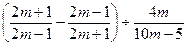 2. Найдите значение выражения:
2. Найдите значение выражения:
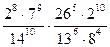 3. Представьте степень с дробным показателем в виде корня
3. Представьте степень с дробным показателем в виде корня
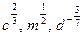 4. Привести указанное выражение к виду
4. Привести указанное выражение к виду 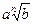 , где а -рациональное число, b – натуральное число , где а -рациональное число, b – натуральное число
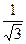 , , 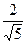 5. Упростить:
5. Упростить:
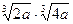 ; ; 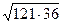 6. Замените арифметические корни степенями с дробным показателем
6. Замените арифметические корни степенями с дробным показателем
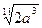 , , 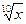 , , 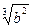 7. Представьте выражение в виде дроби, знаменатель которой не содержит знака корня
7. Представьте выражение в виде дроби, знаменатель которой не содержит знака корня
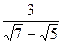 10. Выполните действие:
8. Сократите дробь 10. Выполните действие:
8. Сократите дробь 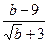 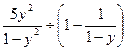 9. Выполните действие
9. Выполните действие 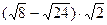
| ВАРИАНТ - II
1. Упростите выражение:
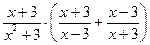 2. Найдите значение выражения:
2. Найдите значение выражения:
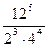 3. Представьте степень с дробным показателем в виде корня
3. Представьте степень с дробным показателем в виде корня
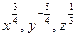 4. Привести указанное выражение к виду
4. Привести указанное выражение к виду 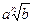 , где а- рациональное число, b – натуральное число , где а- рациональное число, b – натуральное число
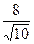 , , 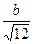 5. Упростить:
5. Упростить:
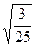 ; ; 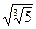 6. Замените арифметические корни степенями с дробным показателем
6. Замените арифметические корни степенями с дробным показателем
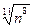 , , 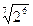 , , 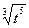 7. Представьте выражение в виде дроби, знаменатель которой не содержит знака корня
7. Представьте выражение в виде дроби, знаменатель которой не содержит знака корня
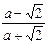 10. Выполните действие:
8. Сократите дробь 10. Выполните действие:
8. Сократите дробь 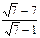 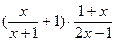 9. Выполните действие
9. Выполните действие 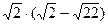
|
ВАРИАНТ - III
1. Выполните действие:
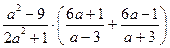 2. Найдите значение выражения:
2. Найдите значение выражения:
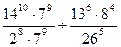 3. Представьте степень с дробным показателем в виде корня
3. Представьте степень с дробным показателем в виде корня
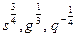 4. Привести указанное выражение к виду
4. Привести указанное выражение к виду 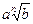 , где а -рациональное число, b – натуральное число , где а -рациональное число, b – натуральное число
 , , 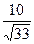 5. Упростить:
5. Упростить:
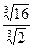 ; ; 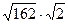 6. Замените арифметические корни степенями с дробным показателем
6. Замените арифметические корни степенями с дробным показателем
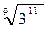 , , 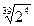 , , 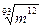 7. Представьте выражение в виде дроби, знаменатель которой не содержит знака корня
7. Представьте выражение в виде дроби, знаменатель которой не содержит знака корня
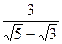 10. Выполните действие:
8. Сократите дробь 10. Выполните действие:
8. Сократите дробь 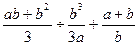
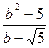 9. Выполните действие
9. Выполните действие
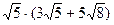
| ВАРИАНТ - IV
1. Выполните действие:
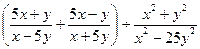 2. Найдите значение выражения:
2. Найдите значение выражения:
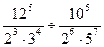 3. Представьте степень с дробным показателем в виде корня
3. Представьте степень с дробным показателем в виде корня
 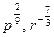 , , 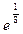 4. Привести указанное выражение к виду
4. Привести указанное выражение к виду 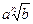 , где а- рациональное число, b – натуральное число , где а- рациональное число, b – натуральное число
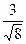 , , 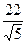 5. Упростить:
5. Упростить:
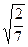 ; ; 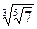 6. Замените арифметические корни степенями с дробным показателем
6. Замените арифметические корни степенями с дробным показателем
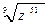 , , 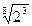 , , 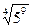 7. Представьте выражение в виде дроби, знаменатель которой не содержит знака корня
7. Представьте выражение в виде дроби, знаменатель которой не содержит знака корня
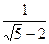 10. Выполните действие:
8. Сократите дробь 10. Выполните действие:
8. Сократите дробь 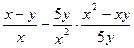
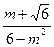 9. Выполните действие
9. Выполните действие
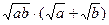
|
ВАРИАНТ - V
1. Упростите выражение:
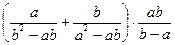 2. Найдите значение выражения:
2. Найдите значение выражения:
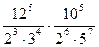 3. Представьте степень с дробным показателем в виде корня
3. Представьте степень с дробным показателем в виде корня
 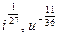 , , 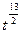 4. Привести указанное выражение к виду
4. Привести указанное выражение к виду 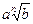 , где а- рациональное число, b – натуральное число , где а- рациональное число, b – натуральное число
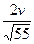 , , 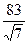 5. Упростить:
5. Упростить:
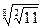 ; ; 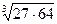 6. Замените арифметические корни степенями с дробным показателем
6. Замените арифметические корни степенями с дробным показателем
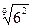 , , 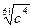 , , 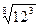 7. Представьте выражение в виде дроби, знаменатель которой не содержит знака корня
7. Представьте выражение в виде дроби, знаменатель которой не содержит знака корня
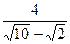 10. Выполните действие:
8. Сократите дробь 10. Выполните действие:
8. Сократите дробь 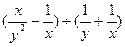
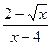 9. Выполните действие
9. Выполните действие
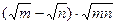
| ВАРИАНТ - VI
1. Упростите выражение:
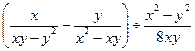 2. Найдите значение выражения:
2. Найдите значение выражения:
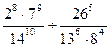 3. Представьте степень с дробным показателем в виде корня
3. Представьте степень с дробным показателем в виде корня
 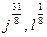 , , 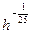 4. Привести указанное выражение к виду
4. Привести указанное выражение к виду 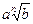 , где -а рациональное число, b – натуральное число , где -а рациональное число, b – натуральное число
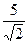 , , 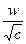 5. Упростить:
5. Упростить:
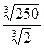 ; ; 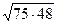 6. Замените арифметические корни степенями с дробным показателем
6. Замените арифметические корни степенями с дробным показателем
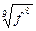 , , 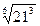 , , 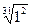 7. Представьте выражение в виде дроби, знаменатель которой не содержит знака корня
7. Представьте выражение в виде дроби, знаменатель которой не содержит знака корня
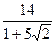 10. Выполните действие
8. Сократите дробь 10. Выполните действие
8. Сократите дробь 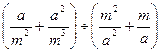
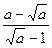 9. Выполните действие
9. Выполните действие
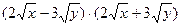
|
Практическое занятие №5
Выполнение преобразований со степенями с рациональным показателем
| Вариант 1 | Вариант 2 |
Задание 1. Вычислить:
а) 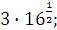 б) б) 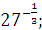 в) в) 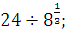 г)
г)  д) д) 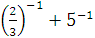 .
Задание 2. Вычислить:
а) .
Задание 2. Вычислить:
а) 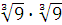 ; б) ; б) 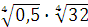 ; в) ; в) 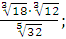 г)
г) 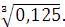 Задание 3. Найдите значение выражения
Задание 3. Найдите значение выражения 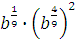 при при 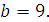 Задание 4. Найдите значение выражения
Задание 4. Найдите значение выражения 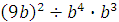 при при 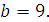 Задание 5. Найдите значение выражения
Задание 5. Найдите значение выражения 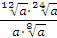 при при 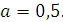 Задание 6. Вычислить:
Задание 6. Вычислить: 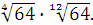
| Задание 1. Вычислить:
а) 5 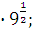 б) б) 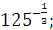 в) 81 в) 81 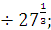 г)
г) 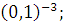 д) д) 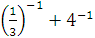 .
Задание 2. Вычислить:
а) .
Задание 2. Вычислить:
а) 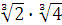 ; б) ; б) 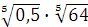 ;
в) ;
в) 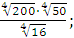 г) г) 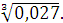 Задание 3. Найдите значение выражения
Задание 3. Найдите значение выражения 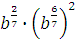 при при 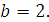 Задание 4. Найдите значение выражения
Задание 4. Найдите значение выражения 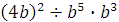 при при 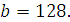 Задание 5. Найдите значение выражения
Задание 5. Найдите значение выражения 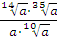 при при 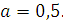 Задание 6. Вычислить:
Задание 6. Вычислить: 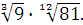
|
| Вариант 3 | Вариант 4 |
Задание 1. Вычислить:
а) 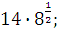 б) б) 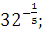 в) в) 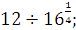 г)
г) 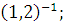 д) д) 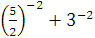 .
Задание 2. Вычислить:
а) .
Задание 2. Вычислить:
а) 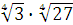 ; б) ; б) 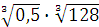 ;
в) ;
в) 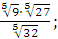 г) г) 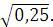 Задание 3. Найдите значение выражения
Задание 3. Найдите значение выражения 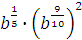 при при 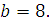 Задание 4. Найдите значение выражения
Задание 4. Найдите значение выражения 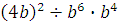 при при 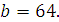 Задание 5. Найдите значение выражения
Задание 5. Найдите значение выражения 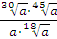 при при 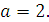 Задание 6. Вычислить:
Задание 6. Вычислить: 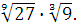
| Задание 1. Вычислить:
а) 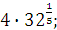 б) б) 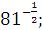 в) 3 в) 3 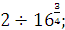 г)
г) 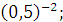 д) д) 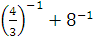 .
Задание 2. Вычислить:
а) .
Задание 2. Вычислить:
а)  ; б) ; б) 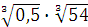 ;
в) ;
в) 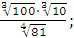 г) г) 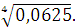 Задание 3. Найдите значение выражения
Задание 3. Найдите значение выражения 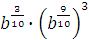 при при 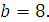 Задание 4. Найдите значение выражения
Задание 4. Найдите значение выражения 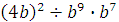 при при 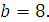 Задание 5. Найдите значение выражения
Задание 5. Найдите значение выражения 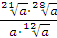 при при 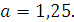 Задание 6. Вычислить:
Задание 6. Вычислить: 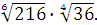
|
| Вариант 5 | Вариант 6 |
Задание 1. Вычислить:
а) 7 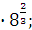 б) б) 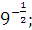 в) в) 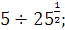 г)
г) 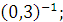 д) д) 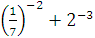 .
Задание 2. Вычислить:
а) .
Задание 2. Вычислить:
а) 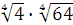 ; б) ; б) 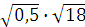 ; в) ; в) 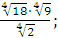 г)
г) 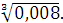 Задание 3. Найдите значение выражения
Задание 3. Найдите значение выражения 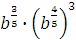 при при 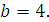 Задание 4. Найдите значение выражения
Задание 4. Найдите значение выражения 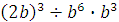 при при 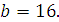 Задание 5. Найдите значение выражения
Задание 5. Найдите значение выражения 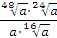 при при 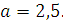 Задание 6. Вычислить:
Задание 6. Вычислить: 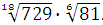
| Задание 1. Вычислить:
а) 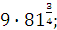 б) б) 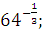 в) в) 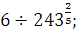 г)
г) 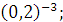 д) д) 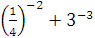 .
Задание 2. Вычислить:
а) .
Задание 2. Вычислить:
а) 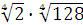 ; б) ; б) 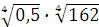 ;
в) ;
в) 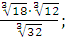 г) г) 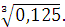 Задание 3. Найдите значение выражения
Задание 3. Найдите значение выражения 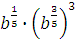 при при 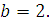 Задание 4. Найдите значение выражения
Задание 4. Найдите значение выражения 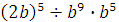 при при 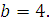 Задание 5. Найдите значение выражения
Задание 5. Найдите значение выражения 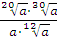 при при 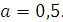 Задание 6. Вычислить:
Задание 6. Вычислить: 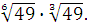
|
| Вариант 7 | Вариант 8 |
Задание 1. Вычислить:
а) 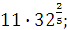 б) б) 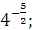 в) в) 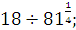 г)
г) 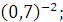 д) д) 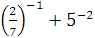 .
Задание 2. Вычислить:
а) .
Задание 2. Вычислить:
а) 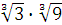 ; б) ; б) 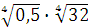 ; в) ; в) 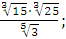 г)
г) 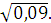 Задание 3. Найдите значение выражения
Задание 3. Найдите значение выражения 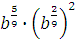 при при  Задание 4. Найдите значение выражения
Задание 4. Найдите значение выражения 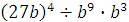 при при 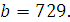 Задание 5. Найдите значение выражения
Задание 5. Найдите значение выражения 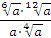 при при 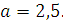 Задание 6. Вычислить:
Задание 6. Вычислить: 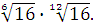
| Задание 1. Вычислить:
а) 10 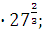 б) б) 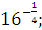 в) в) 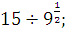 г)
г) 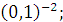 д) д) 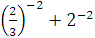 .
Задание 2. Вычислить:
а) .
Задание 2. Вычислить:
а) 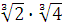 ; б) ; б) 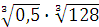 ;
в) ;
в) 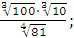 г) г) 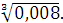 Задание 3. Найдите значение выражения
Задание 3. Найдите значение выражения 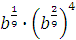 при при 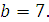 Задание 4. Найдите значение выражения
Задание 4. Найдите значение выражения 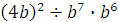 при при 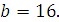 Задание 5. Найдите значение выражения
Задание 5. Найдите значение выражения 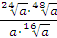 при при 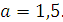 Задание 6. Вычислить:
Задание 6. Вычислить: 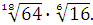
|
Практическое занятие № 6
Выполнение заданий на нахождение значений логарифмов
Цели урока:
образовательные
· повторить определение логарифма, основные логарифмические соотношения
· совершенствовать умения и навыки логарифмирования
· формировать и развивать навыки применения свойств логарифмов при нахождении значений логарифмических выражений
· совершенствовать вычислительные навыки
· развивающие
· развивать логическое мышление
· развивать усидчивость и трудолюбие
· развивать память и внимание
Задание 1.
1.Логарифмом _________________________числа b по основанию а называется _________________________, в которую надо возвести ____, чтобы получить ____
(где а…., а….)
2.Логарифм числа b по основанию 10 называется ___________________и обозначается_______
3.Логарифм числа b по основанию е называется ___________________и обозначается_______
4.Действие нахождения значения логарифма называется __________________________
5.Закончите запись:
1) 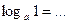
2) 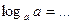
3) 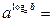 …
…
4) 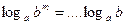
5) 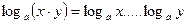
6) 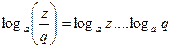
7) 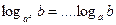
8) 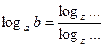
Задание 2.
1. 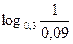 6.
6. 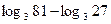
2. 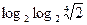 7.
7. 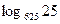
3. 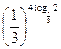 8.
8. 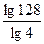
4. 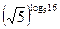 9.
9. 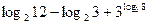
5. 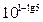 10
10 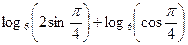
Задание 3.
1 вариант
а) 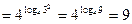
б) 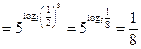
в) 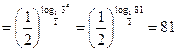
г) 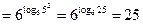
2 вариант
а) 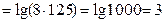
 б)
б) 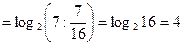
в) 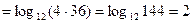 г)
г) 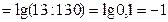
3 вариант
а) 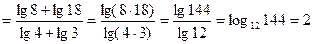
б) 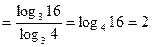
в) 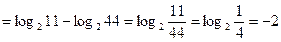
г) 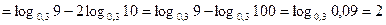
Задание 4.
А1 Вычислите: 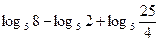
1) 100 2) 25 3) 12,25 4) 2
А2 Укажите значение выражения: 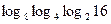
1) 0 2) 1 3) 4 4) 8
А3 Вычислите: 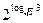
1) 3 2) 6 3) 9 4) 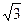
А4.Укажите значение выражения: 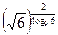
1) 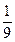 2) 6 3)
2) 6 3) 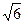 4) 9
4) 9
А5.Укажите значение выражения 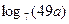 , если
, если
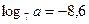
1) -10,6 2) -17,2 3) -6,6 4) -57,6
А6.Укажите значение выражения 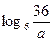 , если
, если
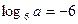
1) 4 2) 8 3) 6 4) -6
В1.Найдите значение выражения:
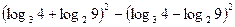 Ответ_____
Ответ_____
В2.Найдите значение выражения :
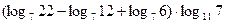 Ответ_____
Ответ_____
Практическое занятие № 7
Выполнение заданий на замену основания логарифмов
Цели:
знать:
определение логарифма;
свойства логарифма.
уметь:
преобразовывать выражения, содержащие логарифм.
Общие сведения и примеры выполнения заданий:
При выполнении заданий по данной теме нужно помнить:
1. Определение логарифма: 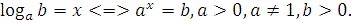
2. Основное логарифмическое свойство: 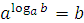 .
.
3. Десятичный логарифм (по основанию 10): 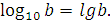
4. Натуральный логарифм (по основанию 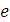 ):
): 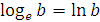 .
.
5. Свойства логарифмов:
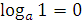
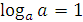
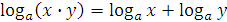
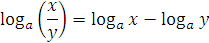
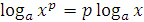
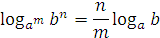
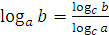 – переход к новому основанию.
– переход к новому основанию.
6. Свойства степени и корней.
7. Таблицу квадратов.
Задание 1
1. Вычислите: 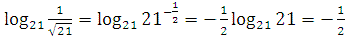 ;
; 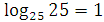 ;
;
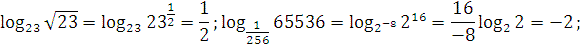
2. Вычислите: 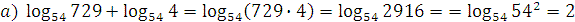 ;
;
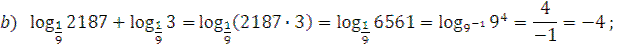
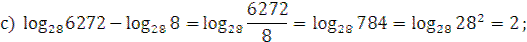
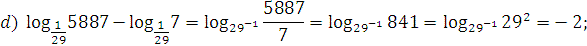
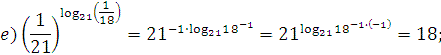
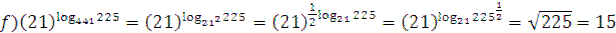
3. Вычислить: 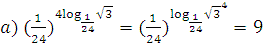 ;
;
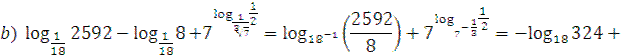
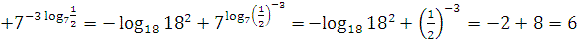 ;
; 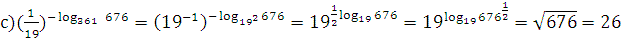
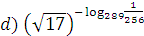 =
= 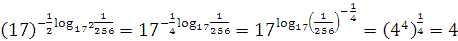 ;
;
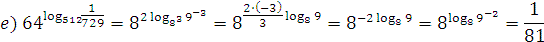
4. Вычислить:
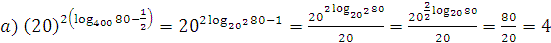 ;
;
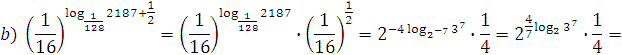
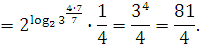
Задание 2
1. Вычислите: 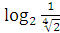 ;
; 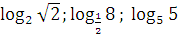
2. Вычислите: 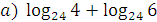 ;
; 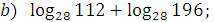
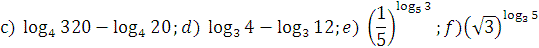
3. Вычислить: 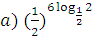 ;
; 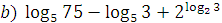 ;
;
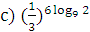 ;
; 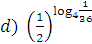 ;
; 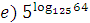
4. Вычислить: 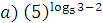 ;
; 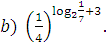
Контрольные вопросы:
1. Определение логарифма.
2.Перечислите основные свойства логарифма.
3. Формулы сокращенного умножения.
Практическое занятие № 8
Выполнение заданий на потенцирование логарифмических выражений
Цель работы:
Нахождение значения показательно-логарифмических выражений, логарифмирование и потенцирование выражений.
Определение логарифма
Логарифм положительного числа 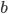 по основанию
по основанию 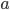 (обозначается
(обозначается 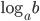 ) — это показатель степени, в которую надо возвести
) — это показатель степени, в которую надо возвести 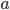 , чтобы получить
, чтобы получить 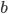 . b > 0, a > 0, а≠ 1.
. b > 0, a > 0, а≠ 1.
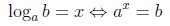 ,
, 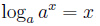
Пример:
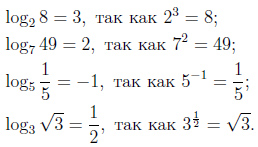
Десятичный логарифм — логарифм с основанием 10, который обозначается как 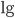 .
.
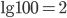 ,
, 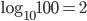 , так как
, так как 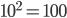
Натуральный логарифм — логарифм с основанием 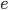 , обозначается
, обозначается 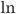
Свойства логарифма

| 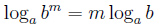
| |
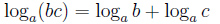
| 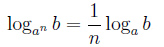
| 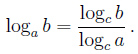
|
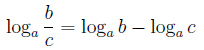
| 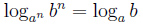
| 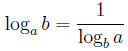
|
Дата: 2018-12-21, просмотров: 519.