ЛЕКЦИЯ 16. 19.12.2018 - разбор тестов из рабочих программ.
ЛЕКЦИЯ 17. 26.12.2018 - обзорная лекция по доказательствам.
Приложение 1. Список доказательств в билеты.
(ДОК 1). Вывести формулу поверхностного интеграла 2 рода:
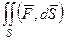 =
= 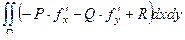 .
.
(ДОК 2) Докажите формулу Грина: 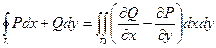 .
.
(ДОК 3) Доказать, что криволинейный интеграл 2 рода не зависит от пути  циркуляция по замкнутому контуру равна 0.
циркуляция по замкнутому контуру равна 0.
(ДОК 4) Доказать, что поле F потенциально 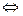 криволинейный интеграл 2 рода от F не зависит от пути.
криволинейный интеграл 2 рода от F не зависит от пути.
(ДОК 5) Доказать, что поле F потенциально 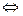 симметрична производная матрица.
симметрична производная матрица.
(ДОК 6) Докажите формулу Остроградского-Гаусса: 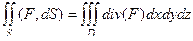 .
.
(ДОК 7) Докажите, что 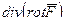 =0,
=0, 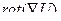 = 0.
= 0.
(ДОК 8).Докажите формулы 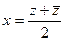 ,
, 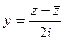
(ДОК 9). Докажите формулу Эйлера 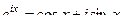 .
.
(ДОК 10) Докажите формулы: 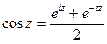 ,
, 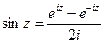 .
.
(ДОК 11) Докажите формулу логарифма  .
.
(ДОК 12). Доказать что линейное отображение  в комплексной плоскости есть композиция растяжения, поворота и сдвига.
в комплексной плоскости есть композиция растяжения, поворота и сдвига.
(ДОК 13). Докажите теорему: Функция 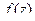 дифференцируема
дифференцируема 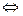
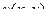 и
и 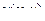 дифференцируемы и выполняются условия Коши-Римана:
дифференцируемы и выполняются условия Коши-Римана: 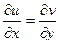 и
и 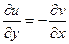 .
.
(ДОК 14). Докажите, что 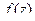 дифференцируемая функция
дифференцируемая функция 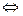 векторные поля
векторные поля 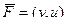 и
и 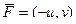 потенциальны.
потенциальны.
(ДОК 15). Если функция является аналитической в некоторой области D, то для каждой из её частей (действительной и мнимой) 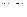 в этой области выполняется уравнение Лапласа:
в этой области выполняется уравнение Лапласа:
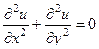 и
и 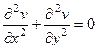 .
.
(ДОК 16). Доказать, что условия Коши-Римана эквивалентны условию  .
.
(ДОК 17). Докажите, что если 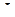 замкнутый контур, внутри которого во всех точках
замкнутый контур, внутри которого во всех точках 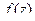 является аналитической, то
является аналитической, то 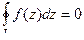 .
.
(ДОК 18). Докажите, что если 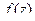 является аналитической во всех точках некоторой области
является аналитической во всех точках некоторой области 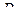 , граница которой односвязна, то интеграл от функции
, граница которой односвязна, то интеграл от функции 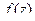 не зависит от пути, то есть имеет одно и то же значение для любой кривой
не зависит от пути, то есть имеет одно и то же значение для любой кривой 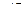 , соединяющей пару точек
, соединяющей пару точек 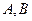 .
.
(ДОК 19). Докажите, что функция 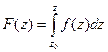 является первообразной от функции
является первообразной от функции 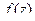 .
.
(ДОК 20). Докажите, что для аналитической на кривой 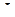 функции верна формула Ньютона-Лейбница:
функции верна формула Ньютона-Лейбница:  .
.
(ДОК 21). Доказать интегральную теорему Коши о том, что 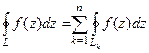 .
.
(ДОК 22). Доказать интегральную формулу Коши: 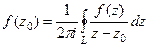
(ДОК 23). Доказать обобщённую интегральную формулу Коши: 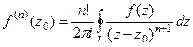 .
.
(ДОК 24). Доказать теорему о разложении функции в ряд Тейлора.
(ДОК 25). Доказать теорему о разложении функции в ряд Лорана.
(ДОК 26). Доказать, что не существует числовой системы нечётной размерности без делителей нуля.
(ДОК 27). Доказать теорему о виде ряда Тейлора в окрестности нуля порядка m.
(ДОК 28). Доказать теорему об изолированности нулей.
(ДОК 29). Теорема о взаимосвязи типа особой точки и строения ряда Лорана.
(ДОК 30). Доказать теорему: Если 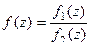 , причём точка
, причём точка 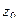 является нулём порядка m для функции
является нулём порядка m для функции 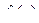 , и нулём порядка n для функции
, и нулём порядка n для функции 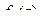 , то при
, то при 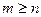 точка
точка 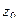 устранимая или правильная точка, а при
устранимая или правильная точка, а при 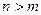 полюс порядка
полюс порядка 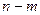 для функции
для функции 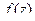 .
.
(ДОК 31). Доказать формулу вычисления вычета для полюса 1-го порядка: 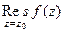 =
= 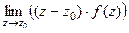 .
.
(ДОК 32). Доказать, что если функция имеет вид  , где
, где 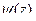 имеет нуль 1 порядка в точке
имеет нуль 1 порядка в точке 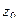 , а
, а 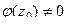 , то
, то 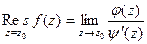 .
.
(ДОК 33). Доказать, что если 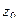 - полюс порядка m, то верна
- полюс порядка m, то верна
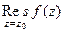 =
= 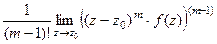 .
.
(ДОК 34). Доказать, что если  устранимая особая точка, то:
устранимая особая точка, то:
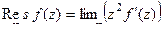
(ДОК 35). Доказать, что если 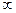 является полюсом порядка m, то:
является полюсом порядка m, то:
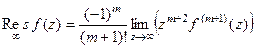
(ДОК 36). Доказать, что 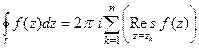 .
.
(ДОК 37). Доказать, что 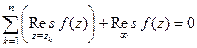 .
.
Дата: 2018-12-21, просмотров: 347.