Если 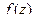 является аналитической на некотором замкнутом контуре
является аналитической на некотором замкнутом контуре 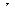 и в односвязной области внутри него, за исключением конечного количества изолированных особых точек, то
и в односвязной области внутри него, за исключением конечного количества изолированных особых точек, то
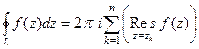 .
.
Доказательство (ДОК 36). По интегральной теореме Коши (стр. 58), интеграл по контуру 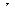 равен сумме интегралов по n контурам внутри него.
равен сумме интегралов по n контурам внутри него.
Тогда 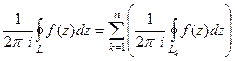 . Но каждое слагаемое в этой сумме - интеграл по контуру вокруг одной особой точки, делённый на
. Но каждое слагаемое в этой сумме - интеграл по контуру вокруг одной особой точки, делённый на
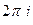 , а по определению это и есть вычет в данной точке
, а по определению это и есть вычет в данной точке 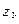 .
.
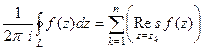
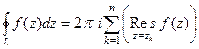 .
.
Вот и получается, что интеграл равен такой величине: 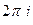 умножить на сумму вычетов.
умножить на сумму вычетов.
Теорема 9. Если 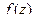 является аналитической во всей комплексной плоскости, за исключением конечного количества изолированных особых точек, то
является аналитической во всей комплексной плоскости, за исключением конечного количества изолированных особых точек, то 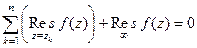 .
.
(Сумма вычетов во всех конечных особых точках + вычет в бесконечности равно 0).
Доказательство (ДОК 37). Если в плоскости конечное количество особых точек, то среди них есть самая далёкая от начала координат. Тогда их все можно включить в круг некоторого радиуса. Ограничим все n особых точек замкнутым контуром 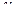 настолько большого радиуса
настолько большого радиуса 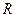 , чтобы все они лежали внутри круга
, чтобы все они лежали внутри круга 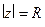 .
.
По определению вычета в 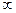 ,
, 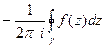 =
= 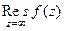 ,
,
а по прошлой теореме 8, 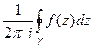 =
= 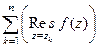 .
.
Получается, что вычет в 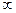 противоположен сумме всех вычетов в конечных особых точках. Складывая эти 2 равенства, мы как раз и получим
противоположен сумме всех вычетов в конечных особых точках. Складывая эти 2 равенства, мы как раз и получим 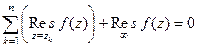 .
.
В следующем примере будет видно разнообразие способов вычисление вычета в 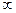 : и по доказанным формулам, и с помощью перехода к конечным точкам, и с помощью коэффициента из ряда Лорана.
: и по доказанным формулам, и с помощью перехода к конечным точкам, и с помощью коэффициента из ряда Лорана.
Пример. Найти 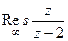 .
.
Способ 1. С помощью формулы из теоремы 6.
Так как 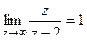 то
то 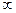 устранимая точка. Тогда можно вычислить по формуле:
устранимая точка. Тогда можно вычислить по формуле: 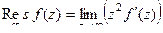 . Итак,
. Итак, 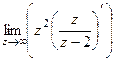 =
=
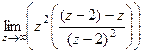 =
= 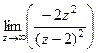 =
= 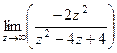 =
=
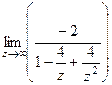 =
=  .
.
Обратите внимание, что по определению вычет это интеграл по ограниченному контуру, т.е. он не может получиться равным 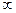 . При правильном вычислении производной, степени числителя и знаменателя уравниваются и предел получается конечный.
. При правильном вычислении производной, степени числителя и знаменателя уравниваются и предел получается конечный.
Способ 2. С помощью теоремы 9 (через конечную точку).
Заметим, что в знаменателе только 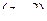 , т.е. эта функция имеет всего лишь одну конечную особую точку. Тогда:
, т.е. эта функция имеет всего лишь одну конечную особую точку. Тогда:
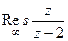 =
= 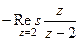 . То есть надо найти вычет в точке 2 и сменить знак.
. То есть надо найти вычет в точке 2 и сменить знак. 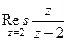 =
= 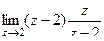 =
= 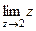 = 2. Поэтому
= 2. Поэтому 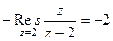 . Получается такой же ответ, как и прошлым методом.
. Получается такой же ответ, как и прошлым методом.
Способ 3. С помощью ряда Лорана.
Разложим 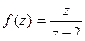 в ряд Лорана в области
в ряд Лорана в области 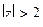 . При этом надо воспользоваться формулой суммы бесконечной убывающей прогрессии:
. При этом надо воспользоваться формулой суммы бесконечной убывающей прогрессии: 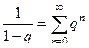 . Так как
. Так как 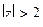 (рассматриваем окрестность бесконечности, а не нуля) то надо, чтобы получалось
(рассматриваем окрестность бесконечности, а не нуля) то надо, чтобы получалось 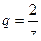 , оно по модулю меньше 1. Но ни в коем случае не
, оно по модулю меньше 1. Но ни в коем случае не 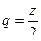 .
.
Итак, 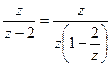 =
= 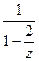 =
= 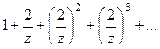 . Выберем коэффициент
. Выберем коэффициент 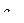 при
при 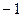 -й степени. Он равен 2. Тогда вычет равен
-й степени. Он равен 2. Тогда вычет равен 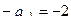 .
.
Файл по состоянию на 10.11.2018
Оставшиеся лекции:
ЛЕКЦИЯ 11. 14.11.2018 Приложения вычетов
ЛЕКЦИЯ 12. 21.11.2018 Вычеты и ряды
ЛЕКЦИЯ 13. 28.11.2018 Ряды Фурье
ЛЕКЦИЯ 14. 05.12.2018 Ряды Фурье
Дата: 2018-12-21, просмотров: 361.