Задумаемся над таким вопросом, можно ли обобщить комплексные числа, например, создать систему с двумя мнимыми единицами и числами вида 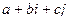 .
.
В системе комплексных чисел задана так называемая в алгебре билинейная операция умножения векторов плоскости. Линейное отображение, которое мы раньше ещё называли линейный оператор, переводит 1 вектор в 1 вектор: 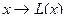 . Билинейное отображение даёт результат для пары объектов,
. Билинейное отображение даёт результат для пары объектов, 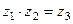 . Так как выполняется дистрибутивность, то есть можно раскрыть скобки в случае, когда объект на первом или втором месте есть сумма двух других, то отображение линейно по каждому аргументу, поэтому оно и называется билинейным.
. Так как выполняется дистрибутивность, то есть можно раскрыть скобки в случае, когда объект на первом или втором месте есть сумма двух других, то отображение линейно по каждому аргументу, поэтому оно и называется билинейным.
При фиксировании одного из элементов, получается действие только на 2-й элемент, т.е. линейное отображение (линейный оператор) действующий по закону 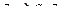 . Например, умножение на
. Например, умножение на 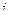 в комплексной плоскости приводит к повороту на 900.
в комплексной плоскости приводит к повороту на 900.
Если линейный оператор задаётся плоской квадратной матрицей порядка n, то для билинейной операции фактически можно построить n линейных операторов: умножение на 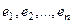 . Тогда в итоге получается объёмная матрица из n3 элементов.
. Тогда в итоге получается объёмная матрица из n3 элементов.
Например, чтобы задать умножение в комплексной плоскости, надо задать умножения всех базисных элементов друг на друга. Можно это записать в виде символьной таблицы:
| 1 | 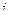
| |
| 1 | 1 | 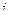
|
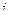
| 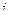
| 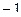
|
Если записать в векторном виде, используя обозначения 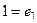 ,
, 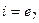 , то есть не акцентируя на том что это комплексная плоскости, а просто в общем виде как действия с геометрическими векторами плоскости, то таблица запишется так:
, то есть не акцентируя на том что это комплексная плоскости, а просто в общем виде как действия с геометрическими векторами плоскости, то таблица запишется так:
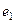
| 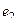
| |
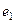
| 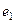
| 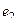
|
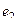
| 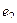
| 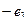
|
Но можно записать подробнее, учитывая все кординаты (те, которых нет, соответствуют 0):
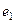
| 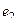
| |
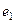
| 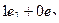
| 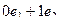
|
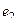
| 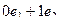
| 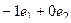
|
Но фактически здесь 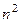 векторов, а значит
векторов, а значит 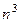 констант. Если откладывать вниз координаты каждого вектора, а в верхнем слое поместить основание матрицы, то получится вот такая 3-мерная матрица:
констант. Если откладывать вниз координаты каждого вектора, а в верхнем слое поместить основание матрицы, то получится вот такая 3-мерная матрица:
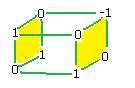
Рассмотрим две матрицы, являющиеся сечениями - они выделены жёлтым. Это линейный оператор умножения на 1 и умножения на 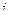 . И здесь одна матрица единичная (задаёт тождественный оператор) а вторая задаёт поворот плоскости на 900.
. И здесь одна матрица единичная (задаёт тождественный оператор) а вторая задаёт поворот плоскости на 900.
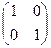 и
и 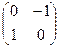 .
.
Докажем, что невозможно задать 3-мерную систему, так, чтобы при этом соблюдались известные базовые арифметические свойства. Например, докажем, что в 3-мерной системе (и в любой системе нечётной размерности) всегда есть делители нуля.
Теорема. Не существует числовой системы нечётной размерности без делителей нуля.
Доказательство (ДОК 26). Допустим, что существует система с двумя мнимыми единицами, где числа вида 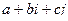 . Умножение на 1 сохраняет любой объект. Отразим это в таблице умножения базисных единиц:
. Умножение на 1 сохраняет любой объект. Отразим это в таблице умножения базисных единиц:
| 1 | 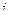
| 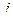
| |
| 1 | 1 | 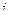
| 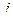
|
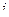
| 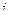
| 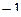
| * |
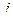
| 
| * | * |
Здесь осталось 3 элемента, помеченных *, которые ещё надо задать, а именно, 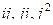 . Как бы мы их не задали, в любом случае, умножение на какой-либо фиксированный элемент данной системы - это линейный оператор в 3-мерном пространстве:
. Как бы мы их не задали, в любом случае, умножение на какой-либо фиксированный элемент данной системы - это линейный оператор в 3-мерном пространстве: 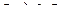 . Ему соответствует какая-то плоская матрица из 9 элементов
. Ему соответствует какая-то плоская матрица из 9 элементов 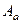 . Существует её определитель
. Существует её определитель 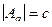 . Таким образом, можно поставить некое число в соответствие каждой точке пространства. Определитель матрицы умножения на данный элемент отождествляет с элементом данной системы, т.е. с точкой 3-мерного пространства. Таким образом, в 3-мерном пространстве задана непрерывная скалярная функция. Но ведь умножение на противоположный элемент
. Таким образом, можно поставить некое число в соответствие каждой точке пространства. Определитель матрицы умножения на данный элемент отождествляет с элементом данной системы, т.е. с точкой 3-мерного пространства. Таким образом, в 3-мерном пространстве задана непрерывная скалярная функция. Но ведь умножение на противоположный элемент 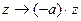 соответствует оператору, у которого матрица состоит из чисел с противоположным знаком. Это матрица
соответствует оператору, у которого матрица состоит из чисел с противоположным знаком. Это матрица 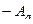 . Так как она порядка 3, то
. Так как она порядка 3, то 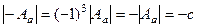 , т.к. коэффициент
, т.к. коэффициент 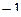 выносится из каждой строки, а их всего 3, нечётное количество. Соединяя точки
выносится из каждой строки, а их всего 3, нечётное количество. Соединяя точки 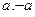 по сфере, получаем дугу, на которой функция изменяется от
по сфере, получаем дугу, на которой функция изменяется от 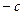 до
до 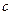 . Тогда существует какая-то точка
. Тогда существует какая-то точка 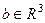 , где данная функция обращается в 0. Таким образом, линейный операторв умножения на
, где данная функция обращается в 0. Таким образом, линейный операторв умножения на 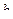 является вырожденным оператором, ведь определитель его матрицы равен 0. А если оператор вырожденный, то существует вектор в пространстве, который отображается в 0. Тогда
является вырожденным оператором, ведь определитель его матрицы равен 0. А если оператор вырожденный, то существует вектор в пространстве, который отображается в 0. Тогда
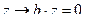 . Таким образом,
. Таким образом, 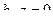 , но
, но 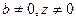 . То есть, в 3-мерной системе обязательно существуют делители нуля - такие ненулевые элементы, которые при умножении порождают 0.
. То есть, в 3-мерной системе обязательно существуют делители нуля - такие ненулевые элементы, которые при умножении порождают 0.
Аналогичное верно и для любой нечётной размерности, так как для неё 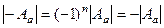 .
.
Кватернионы.
Указанные выше причины не препятствуют построению числовых систем в случае чётной размерности. Так, если сделать по аналогии перехода от действительных чисел к комплексным, удвоить размерность и образовать числа вида 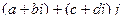 из пары комплексных чисел, где второе умножено ещё на какой-то объект
из пары комплексных чисел, где второе умножено ещё на какой-то объект 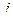 , то получается 4-мерная система с тремя мнимыми единицами и числами вида
, то получается 4-мерная система с тремя мнимыми единицами и числами вида 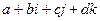 , которые называются кватернионами.
, которые называются кватернионами.
При этом  это мы изначально называем произведение 1-й и 2-й мнимых единиц некоторой третьей мнимой единицей.
это мы изначально называем произведение 1-й и 2-й мнимых единиц некоторой третьей мнимой единицей.
Получается антикоммутативная система с умножением:
 ,
, 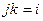 ,
, 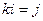 ,
, 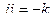 ,
, 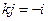 ,
, 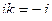 .
.
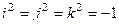 . Умножение на 1 сохраняет любой объект неизменным. Получается таблица:
. Умножение на 1 сохраняет любой объект неизменным. Получается таблица:
Таблица умножения базисных элементов системы кватернионов.
| 1 | 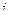
| 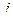
| 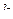
| |
| 1 | 1 | 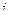
| 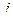
| 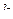
|
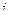
| 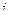
| 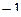
| 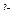
| 
|
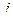
| 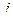
| 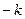
| 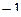
| 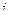
|
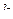
| 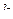
| 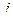
| 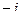
| 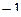
|
Обратите вниание, что законы умножения в системе кватернионов 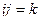 ,
, 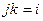 ,
, 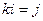 легко запомнить, если представить с помощью цикла:
легко запомнить, если представить с помощью цикла:
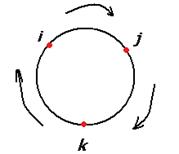
При умножении каждой пары получается следующий, если двигаться строго по часовой стрелке. Ещё обратите внимание, что мнимые единицы системы кватернионов подчиняются таким же законам, как векторное умножение в 3-мерном пространстве. Там тоже 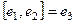 ,
, 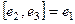 ,
,  . Векторное произведение пары векторов есть общий перпендикулярк ним, причём так чтобы получалась правоориентированная тройка. Векторное умножение было придумано Гамильтоном в 1843 году как раз одновременно с системой кватернионов.
. Векторное произведение пары векторов есть общий перпендикулярк ним, причём так чтобы получалась правоориентированная тройка. Векторное умножение было придумано Гамильтоном в 1843 году как раз одновременно с системой кватернионов.
Как и для комплексных чисел, здесь есть понятие «сопряжённый кватернион». Если 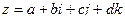 то
то 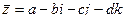 . При этом
. При этом 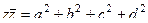 , то есть можно также ввести понятие модуля кватерниона:
, то есть можно также ввести понятие модуля кватерниона: 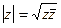 =
= 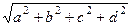 .
.
Подробнее о том, почему получается 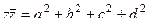 .
.
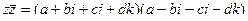 =
=
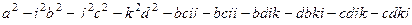 =
=
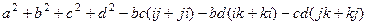 но система антикоммутативна, т.е.
но система антикоммутативна, т.е. 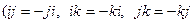 , поэтому все эти суммы в скобках равны 0, вот и остаётся
, поэтому все эти суммы в скобках равны 0, вот и остаётся 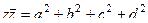 .
.
Дата: 2018-12-21, просмотров: 363.