Нули аналитической функции.
Определение. Точка  называется нулём функции
называется нулём функции 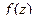 , если
, если 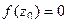 .
.
Мы сначала изучим нули функции, для того, чтобы затем изучить более подробно типы точек разрыва. Если  является нулём для
является нулём для 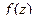 то в этой же точке предел
то в этой же точке предел 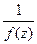 равен
равен 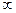 .
.
Вспомним, что в 1 семестре было ещё название «бесконечно-малая» и «бесконечно-большая» функция в точке. Бесконечно-малые могли быть разных порядков. Есть и здесь аналогичное более подробное определение, различающее порядки бесконечно малых:
Определение. Точка  называется нулём порядка m функции
называется нулём порядка m функции 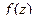 , если
, если 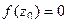 и функция представима в виде
и функция представима в виде 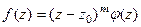 , где
, где 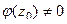 .
.
Кстати, здесь ещё можно напомнить, что для многочленов тоже было известно понятие корня кратности m, и аналогия тут прямая.
Теорема 1. (О виде ряда Тейлора в окрестности нуля порядка m).
Если  нуль порядка m функции
нуль порядка m функции  , то ряд Тейлора имеет вид
, то ряд Тейлора имеет вид
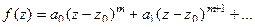 т.е. начинается именно со степени m.
т.е. начинается именно со степени m.
Доказательство (ДОК 27). Если 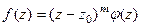 , где
, где 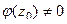 , то ряд Тейлора функции
, то ряд Тейлора функции 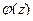 обязательно начинается с константы, а иначе не было бы
обязательно начинается с константы, а иначе не было бы 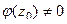 . Тогда:
. Тогда:
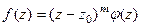 =
= 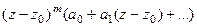
что и приводит к виду 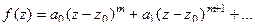
Теорема 2. (Об изолированности нулей).
Если  является нулём порядка m функции
является нулём порядка m функции  , то существует окрестность
, то существует окрестность 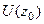 , не содержащая других нулей этой функции.
, не содержащая других нулей этой функции.
Доказательство (ДОК 28). Если  является нулём порядка m функции
является нулём порядка m функции  , то
, то 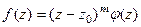 . Первый множитель обращается в 0 только в самой точке
. Первый множитель обращается в 0 только в самой точке  и нигде больше. Второй в точке
и нигде больше. Второй в точке  отличен от 0. Но
отличен от 0. Но 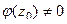 , а так как эта функция аналитическая и значит, непрерывная, то существует окрестность
, а так как эта функция аналитическая и значит, непрерывная, то существует окрестность 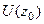 , в которой
, в которой 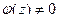 т.е. не обращается в 0 ни в одной её точке. Итак, есть произведение двух множителей, где первый равен 0 только в
т.е. не обращается в 0 ни в одной её точке. Итак, есть произведение двух множителей, где первый равен 0 только в  , а второй нигде в окрестности
, а второй нигде в окрестности 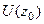 . Таким образом, в
. Таким образом, в 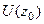 произведение обращается в 0 только в
произведение обращается в 0 только в  .
.
Следствие 1. Если существует последовательность нулей функции, сходящаяся к  , то в некоторой окрестности
, то в некоторой окрестности 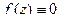 .
.
ЛЕКЦИЯ 9. 31.10.2018
Особые точки
Определение. Точка  называется правильной точкой функции
называется правильной точкой функции  , если
, если  является аналитической в
является аналитической в  , и особой точкой, если она не является аналитической в
, и особой точкой, если она не является аналитической в  .
.
Определение. Точка  называется изолированной особой точкой, если в некоторой её окрестности
называется изолированной особой точкой, если в некоторой её окрестности 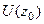 нет других особых точек.
нет других особых точек.
Существует такая классификация особых точек в зависимости от предела  .
.
| Название | Устранимая особая точка | Полюс | Существенно-особая точка |
| При каком условии | 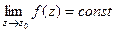
| 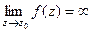
| 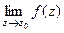 не существует
не существует
|
Пример
( 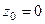 ) )
|  = = 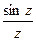
|  = = 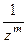
|  = = 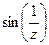
|
Теорема 1. Точка  является нулём функции
является нулём функции 
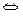 она является полюсом функции
она является полюсом функции 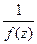 .
.
Доказательство. Точка  является нулём функции
является нулём функции 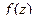
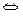 функция
функция 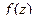 представима в виде
представима в виде 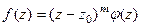 , причём
, причём
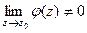 . Это эквивалентно тому, что
. Это эквивалентно тому, что 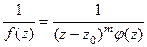 =
=
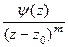 , где
, где 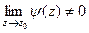 , а предел знаменателя равен 0. Это означает, что
, а предел знаменателя равен 0. Это означает, что 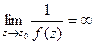 .
.
В связи с этим, естественным образом возникает определение полюса порядка 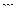 : точка
: точка  называется полюсом порядка m для функции
называется полюсом порядка m для функции  , если для функции
, если для функции 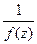 она является нулём порядка m.
она является нулём порядка m.
Теорема 2.
(О взаимосвязи типа особой точки и строения ряда Лорана).
1).  устранимая особая точка
устранимая особая точка 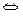 остутствует главная часть ряда Лорана.
остутствует главная часть ряда Лорана.
2)  полюс
полюс 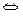 главная часть ряда Лорана содержит конечное количество слагаемых.
главная часть ряда Лорана содержит конечное количество слагаемых.
3)  существенно-особая точка
существенно-особая точка 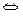 главная часть ряда Лорана содержит бесконечное количество слагаемых.
главная часть ряда Лорана содержит бесконечное количество слагаемых.
Доказательство (ДОК 29). Напомним строение ряда Лорана в окрестности точки  в общем случае:
в общем случае:
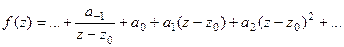
Пункт 1) Если присутствует хотя бы одна отрицательная степень, то 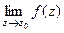 не будет конечным числом. Таким образом, если
не будет конечным числом. Таким образом, если 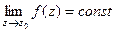 то
то 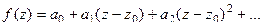 , причём
, причём 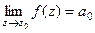 .
.
И обратно, если 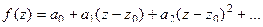 то
то 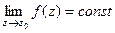 , потому что
, потому что 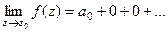 , ведь каждое слагаемое кроме
, ведь каждое слагаемое кроме 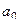 стремится к 0.
стремится к 0.
Пункт 2) Точка  является полюсом порядка m эквивалентно тому, что
является полюсом порядка m эквивалентно тому, что 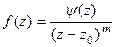 , где функция в числителе имеет ненулевой предел, поэтому её разложение в ряд имеет вид:
, где функция в числителе имеет ненулевой предел, поэтому её разложение в ряд имеет вид: 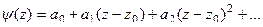
Тогда 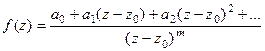 =
=
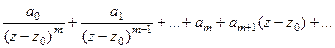 то есть крайняя отрицательная степень это именно число
то есть крайняя отрицательная степень это именно число  если порядок полюса m.
если порядок полюса m.
В главной части может быть не ровно m слагаемых, а какие-то пропущены (коэффициенты 0) но крайнее левое имеет именно степень, равную  .
.
И обратно, если крайняя левая степень  , то можно представить в виде
, то можно представить в виде
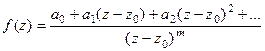 т.е.
т.е. 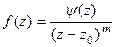 , и тогда точка является полюсом.
, и тогда точка является полюсом.
Пункт 3) Если точка является существенно-особой, но при этом допустить, что главная часть ряда Лорана состоит из нулевого либо из конечного количества слагаемых, то согласно предыдущим пунктам, получали бы противоречие: точка или устранимая, или полюс, и не является существенно-особой. Таким образом, из того, что она существенно-особая, логически следует бесконечность главной части ряда. И обратно, если главная часть бесконечна, то невозможно допустить, что точка полюс или устранимая, иначе сразу получалось бы противоречевое условие, что главная часть конечна.
Пример. Найти все особые точки и указать их тип для 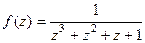 .
.
Решение. Преобразуем знаменатель: 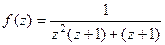 =
=
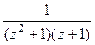 =
= 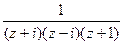 . В знаменателе 3 нуля, причём каждый 1-го порядка, а именно
. В знаменателе 3 нуля, причём каждый 1-го порядка, а именно 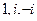 . Следовательно, для функции 3 полюса 1-го порядка:
. Следовательно, для функции 3 полюса 1-го порядка: 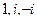 .
.
Пример. Указать тип всех особых точек для функции:
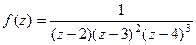 .
.
Решение. В знаментателе нули 1-го, 2-го и 3-го порядка, а именно, точки 2,3 и 4. Тогда для 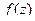 :
: 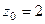 полюс 1-го порядка,
полюс 1-го порядка,
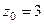 полюс 2-го порядка,
полюс 2-го порядка, 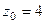 полюс 3-го порядка.
полюс 3-го порядка.
Теорема 3. Если 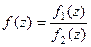 , причём точка
, причём точка  является нулём порядка m для функции
является нулём порядка m для функции 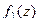 , и нулём порядка n для функции
, и нулём порядка n для функции 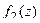 , то при
, то при 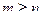 точка
точка  устранимая или правильная точка, а при
устранимая или правильная точка, а при 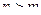 полюс порядка
полюс порядка 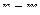 для функции
для функции 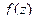 .
.
Доказательство (ДОК 30). Если  - нуль порядка m и n соответственно для числителя и знаменателя, то
- нуль порядка m и n соответственно для числителя и знаменателя, то 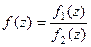 =
= 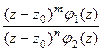 =
= 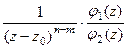 где
где 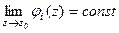 для каждой из двух функций. Тогда можно обозначить
для каждой из двух функций. Тогда можно обозначить 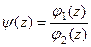 и в итоге
и в итоге  , это и означает, что полюс порядка
, это и означает, что полюс порядка 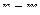 .
.
Пример. Определить тип особой точки 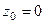 для функции
для функции 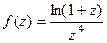 .
.
Решение. Представим функцию в числителе в виде разложения в ряд Тейлора.
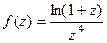 =
= 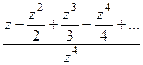 =
= 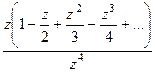 в числителе нуль 1 порядка, а в знаменателе 4-го. Тогда точка
в числителе нуль 1 порядка, а в знаменателе 4-го. Тогда точка  полюс 3 порядка.
полюс 3 порядка.
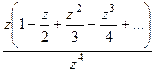 =
= 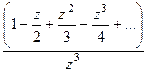 =
= 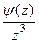 . В числителе после сокращения осталась функция, имеющая ненулевой предел.
. В числителе после сокращения осталась функция, имеющая ненулевой предел.
Дата: 2018-12-21, просмотров: 357.