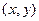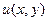Функция  фактически задаёт отображение плоскости в плоскости, то есть пара действительных чисел  отображается в пару чисел .  Для двух функций  и 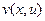 существуют 4 частных производных: .

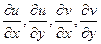Определение производной. Производной функции 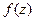 в точке  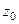называется следующий предел: .

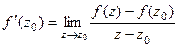Также можно кратко записать в виде .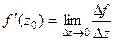

Заметим, что все величины в этой дроби, существуют и вычислимы, ведь здесь частное от разностей комплексных чисел.

Определение дифференцируемости. Функция  называется дифференцируемой в точке , если приращение функции можно представить в ви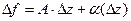де: , где 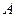 некоторое комплексное число,  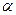- бесконечно малая более высокого порядка, чем .

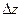Заметим, что если функция дифференцируема, то 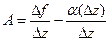 , но тогда т.е.  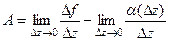тогда , т.е. константа .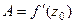

Геометрический смысл производной. Так как с точностью до бесконечно-малой, можно представить 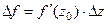, а это линейное отображение, изученное в конце прошлой лекции, то в малой окрестности отображение представимо в виде растяжения и поворота, где  это угол поворота, а  - коэффициент растяжения.

Изучим взаимосвязь дифференцируемости 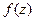 с дифференцируемостью координатных функци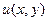й  и .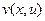

Теорема 1. Функция 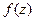 дифференцируема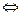 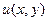 и 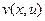 дифференцируемы и выполняются условия Коши-Римана:

 и .

Доказательство (ДОК 13).  Запишем подробнее равенство . .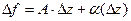

Раскроем скобки и сгруппируем слагаемые, в которых есть и в которых нет мнимой единицы.

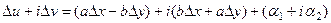
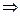
Получается такая система из двух равенств:

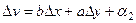
Если в 1-м уравнении рассмотреть приращение только по оси , тогда 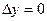, то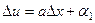   

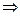
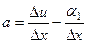
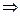
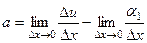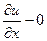 = , так как  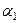бесконечно малая более высокого порядка, так что при делении на величину  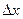первого порядка предел равен 0. Итак, .

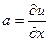Если теперь во 2-м уравнении рассмотреть приращение только по оси 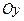, то аналогично получится  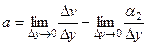= , т.е. 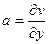. Итак, .

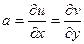По аналогии с этими рассуждениями, если в 1-м равенстве вычислять предел при сдвиге только по оси 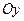, а во 2-м по 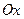, получим

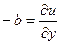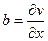, , откуда второе условие Коши-Римана .

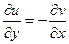А для доказательства достаточности, можно наоборот, сложить два равенства: 

,

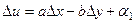
умножив при этом второе на 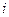. Если выполнены условия Коши-Римана, то 4 коэффициента при этом не являются 4-мя разными числами, а попарно совпадают, то мы как раз и получим:

□

       Вывод. Итак, 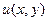 и 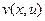 должны быть взаимосвязаны, т.е. если мы произвольно зададим две какие-то функции 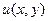,  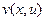и составим из них 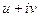, то не всегда получим какую-то дифференцируемую комплексную функцию.

Пример. Проверить выполнение условий Коши-Римана для функции .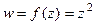

 =  =  = .

, .

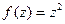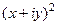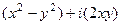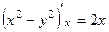,  они равны (1-е условие Коши-Римана).

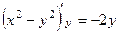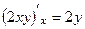,  они противоположны ( а это и есть

2-е условие Коши-Римана).

Теорема 2. 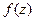 дифференцируемая функция  векторные поля

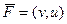 и 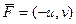 являются потенциальными.

Доказательство (ДОК 14). Вспомним условие потенциальности поля 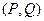, а именно, 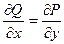. Для векторного поля  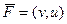в таком случае, , , 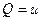и тогда условие потенциальности эквивалентно первому условию Коши-Римана  .

Для векторного поля 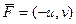 соответственно, 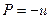, , 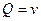и тогда условие потенциальности эквивалентно второму условию Коши-Римана: .

.

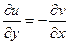Метод вычисления производных по функциям .

Если задано 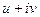 то достаточно вычислить . Производные по  являются излишней информацией, так как они взаимосвязаны с этими производными с помощью условий Коши-Римана. Например, 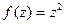 = 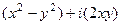. Тогда  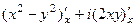= 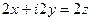, в то же время и .

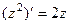А сейчас мы рассмотрим функцию, для которой не выполнены условия Коши-Римана.

Пример. 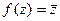. Тогда , 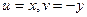. Не выполняется 1-е условие: 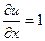, , 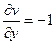они не равны ни в одной точке.

Геометрически это означает, что зеркальное отражение плоскости невозможно представить в виде композиции растяжения и поворота, то есть невозможно равенство из условия дифференцируемости .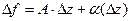

Определение. Если функция дифференцируема и в самой точке 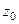, и во всех точках некоторой её окрестности, то она называется аналитической в точке .

Пример. Для функции  условия Коши-Римана выполняются независимо от точки, то есть во всех точках плоскости, тогда для каждой точки они автоматически выполнены и во всей её окрестности. Таким образом,  аналитическая во всех точках комплексной плоскости.

Различие понятий аналитичности и дифференцируемости видно на другом примере.

Пример. 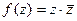. Распишем её через .

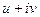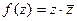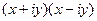 =  = . Здесь , .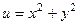

,  .

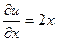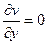1-е условие Коши-Римана выполняется только при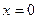

, .

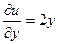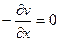2-е условие Коши-Римана выполняется только при .

Таким образом, единственная точка в плоскости, где выполнены условия Коши-Римана, это (0,0). Но ни в одной точке из её окрестности они не выполняются, а только в одной изолированной точке 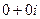. То есть, в начале координат функция дифференцируемая, но не аналитическая.

Теорема 3. Если функция является аналитической в некоторой области D, то для каждой из её частей (действительной и мнимой) 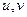 в этой области выполняется уравнение Лапласа:

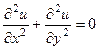 и .

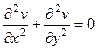Доказательство. (ДОК 15).

Запишем 2 условия Коши-Римана. Одно продифференцируем по переменной , а второе по :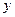

.

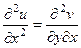
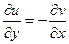
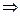
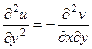Сложим теперь эти 2 равенства, но при этом смешанные производные 2 порядка от 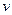 при этом совпадают, они вычитаются и дают 0.

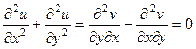. Итак, .

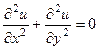Теперь снова запишем условия Коши-Римана, 1-е дифференцирует по , а второе по .

.

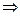
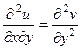
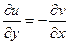
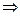
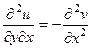Теперь вычтем из 1-го равенства 2-е.

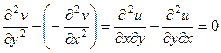, тогда .

□

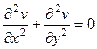Пример. 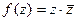 = 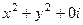. Здесь для  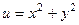не верно уравнение Лапласа: .

Теорема 4. Условия Коши-Римана эквивалентны условию .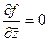

Доказательство (ДОК 16). Вспомним, что  можно выразить через 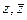 таким образом: 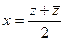, 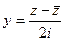. Сделаем это в функциях .

 = .

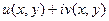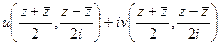Таким образом, функция стала выражена через два аргумента 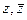, а значит, можно искать частную производную по .

Вспомним формулу полной производной (из 1 семестра) для случая композиции типа : . Найдём производные от 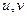 по  этим методом, причём здесь тоже промежуточные переменные .

, .

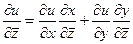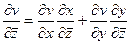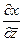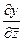При этом такие компоненты как  и  можно найти

из формул 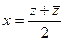, , 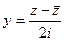а именно : 

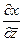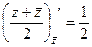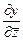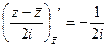 = ,  = . Таким образом,

, .

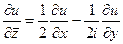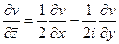Тогда  =  =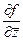

 =  =

 =  .

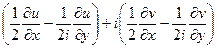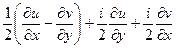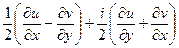Выполнение условий Коши-Римана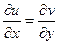

 в данном случае как раз и эквивалентно тому, что в обеих скобках нули, то есть .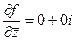

□

Итак, как видим, наличие 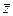 в составе функции приводит к недифференцируемости. Впрочем, то же верно и при наличи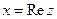и  или 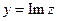, в составе которых есть элемент .