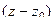В случае, когда в точке  полюс, в знаменателе далеко не всегда  степенная функция, содержащая , возможно, что там произвольная функция. Чтобы вычислять вычет и в этом случае, рассмотрим такой факт.

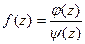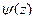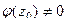Теорема 4. Если функция имеет вид , где  имеет нуль 1 порядка в точке , а , то .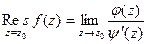

Доказательство (ДОК 32). По предыдущей теореме,

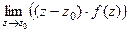= , тогда = 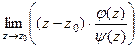, но при этом , так что можно утверждать, что =  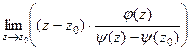= 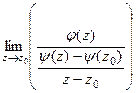, а теперь в знаменателе как раз и есть производная от  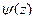в точке . Итак, 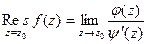, что и требовалось доказать.

Пример. Найти .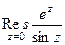

Решение.  =  = .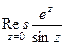

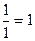Можно было решить и с помощью теоремы 4, 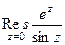 =  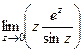=  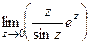= , но в этом случае надо было бы использовать 1-й замечательный предел. 

Выведем формулу для полюса порядка m.

Теорема 5. Если  - полюс порядка m,  то верна формула вычисления вычета:  = .

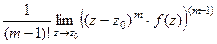Доказательство (ДОК 33). Как и теорему 3, можно доказать двумя методами: с помощью ряда и с помощью интегральной формулы Коши. Здесь остановимся на доказательстве только по интегральной формуле Коши. Запишем обобщённую формулу Коши для какой-нибудь функции 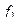, т.к. обозначение  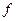у нас уже использовано, оно будет применяться ко всей функции, которая в интеграле.

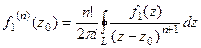. Но ведь мы можем сделать такую замену индекса:  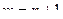и переписать формулу в виде

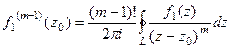 или эквивалентно: 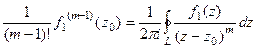.  Пусть . Тогда

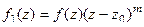, а интегральная формула Коши запишется в виде: 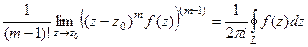= . Правая часть этой формулы по определению как раз и равна вычету .

Пример. Найти вычет .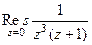

Решение. Здесь точка 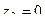 полюс порядка 3, конкретизируем формулу для этого порядка и этой точки:

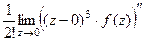= . Итак,  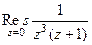=  =  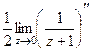=  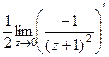=  =  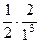= 1.

Пример. Найти вычет .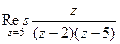

Решение.  Здесь точка  полюс 1 порядка. Поэтому

 =  =  = .

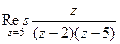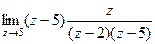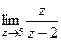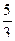Пример. Найти вычет .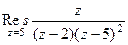

Решение. Здесь точка  полюс 2 порядка. Поэтому

 =  =  =

 =  = .

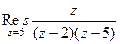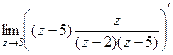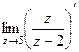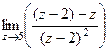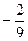Пример. Найти вычет .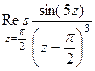

Решение. Здесь точка  полюс 3 порядка. Поэтому

 =  =  =  = .

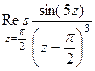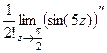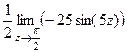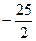Определение вычета в 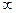. Пусть  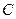замкнутый контур, на контуре и вне его нет особых точек. Тогда интеграл  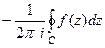называется вычетом функции  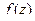в 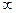 и обозначается .

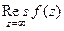Когда мы рассматривали конечную точку , то при вычислении интеграла по контуру обходили его против часовой стрелки, чтобы точка оставалась слева. А чтобы например, линия горизонта (бесконечность) оставалась с левой стороны при движении, нужно круг обходить наоборот, именно по часовой стрелке. Поэтому-то здесь изначально в определении знак минус.

Важно заметить, что при этом 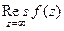 равен 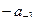, т.е. минус первому коэффициенту ряда Лорана при разложении в окрестности  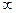(то есть в области 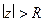) с противоположным знаком.

Пример. Найти вычет .

Решение. Вспомним разложение косинуса в ряд Тейлора:

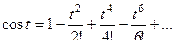Здесь 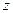 бесконечно-большая величина, а  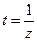наоборот, бесконечно малая, так что переход получается корректный, ведь мы применяем формулу Тейлора как раз в окрестности нуля.

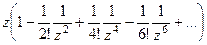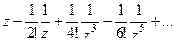 =  =  Теперь выберем коэффициент при  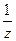и изменим его знак, получится . Ответ. .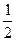

Пример. Найти вычет .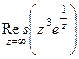

Решение. Вспомним разложение экспоненты в ряд Тейлора:

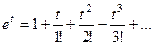Тогда  =

=  =

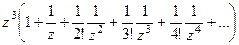Коэффициент при  равен 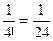, тогда ответ  = .

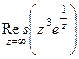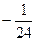Подробнее рассмотрим строение ряда Лорана в окрестности 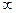. Если для  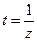полюс порядка m в точке 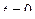, то крайняя отрицательная степень равна . Тогда для ряда Лорана по 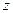, крайняя положительная степень равна . То есть ряд вида

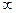. Если  устранимая особая точка, то ряд имеет вид . Но в этом случае коэффициент 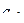 может быть не равен 0. То есть, даже в случае, когда  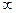 устранимая особая точка, то вычет может быть не равен 0.

Теорема 6. Если 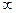 устранимая особая точка, то вычет равен:

Доказательство (ДОК 34). Если 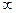 устранимая особая точка, то ряд имеет вид: 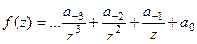. Чтобы коэффициент  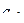оказался крайним и его можно было выразить, продифференцируем 1 раз, и константа  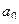исчезнет: 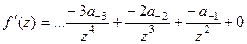. Теперь домножим на 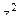, получим . Если перейти к пределу при 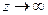, то все слагаемые устремятся к 0, и останется лишь одна константа 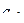, которую мы как раз и хотели выразить. Коэффициент  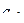с отрицательным знаком в точности равен вычету, поэтому полчили то, что и требовалось доказать:

=  

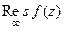
Теорема 7. Если 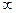 является полюсом порядка m, то вычет равен:

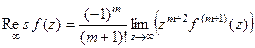
Доказательство (ДОК 35). Если 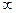 полюс порядка m, то ряд имеет вид: 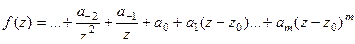. Чтобы коэффициент  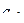оказался крайним и его можно было выразить, надо продифференцировать столько раз, чтобы исчезли все положительные степени. Так, после 1-го дифференцирования:

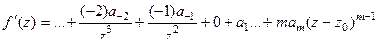
исчезла только константа 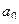. После 2-го исчезнет , а там где была степень m, только после 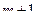- го дифференцирования.

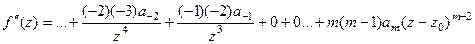
Все положительные степени исчезнут после дифференцирования 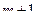 раз. Но более подробно обратим внимание, что при этом происходит с тем коэффициентом, где есть 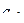. Там каждый раз степень в знаменателе увеличивается, и домножается на следующее отрицательное число. После m шагов получилось бы

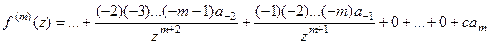где  .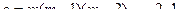

На последнем шаге справа от 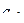 исчезает уже всё полностью, и получается

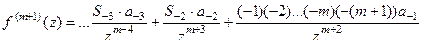
где 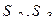 и далее - тоже числовые коэффициенты, состоящие из произведений целых отрицательных чисел. Если домножить на , то получатся все отрицательные степени 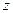, и лишь одна константа, как раз там, где есть .

.

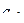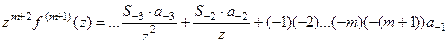Если теперь перейти к пределу при 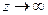, то все слагаемые кроме последнего устремятся к 0.

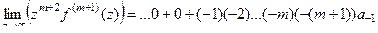 , итак,

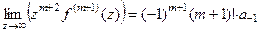. Но для вычета нам надо выразить величину 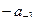, поэтому запишем так:

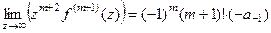. Тогда

. Впрочем, деление на 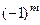 эквивалентно умножению на 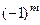, ведь это либо  либо 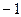. Так что для удобства записи формулы, можно перенести в числитель:

.

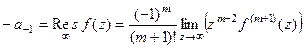Что и требовалось доказать.

Замечание. При 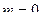 из формулы в теореме 7: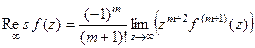

получается формула из теоремы 6: .

полюс порядка  это и есть устранимая точка.