(от скалярных функций).
В прошлом учебном году мы изучали формулы длины кривой и площади поверхности. Напомним их, чтобы ввести понятия криволинейных и поверхностных интегралов.
Формула длины явно заданной кривой: 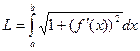 .
.
Для параметрически заданной кривой: 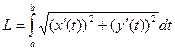 .
.
В трёхмерном пространстве: 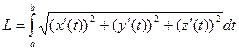 .
.
Площадь поверхности.
Для явно заданной поверхности: 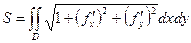 . Коротко напомним идею вывода этой формулы.
. Коротко напомним идею вывода этой формулы.
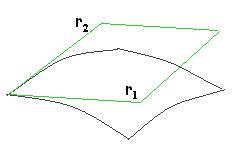
Вектор 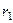 направлен по касательной в сечении, параллельном оси
направлен по касательной в сечении, параллельном оси 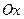 , то есть тангенс угла наклона для него это
, то есть тангенс угла наклона для него это 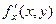 . Его координаты:
. Его координаты: 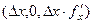 =
= 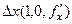 . Аналогично вектор
. Аналогично вектор 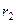 расположен в сечении вдоль оси
расположен в сечении вдоль оси 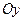 , его координаты
, его координаты 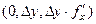 , если вынести дельта, то это
, если вынести дельта, то это 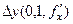 . Площадь параллелограмма вычисляется с помощью векторного произведения, она равна модулю векторного произведения.
. Площадь параллелограмма вычисляется с помощью векторного произведения, она равна модулю векторного произведения.
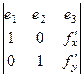 =
= 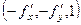 , модуль этого вектора:
, модуль этого вектора: 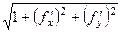 .
.
А в случае параметрического задания поверхности с помощью векторной функции 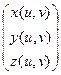 этот определитель приобрёл бы вид
этот определитель приобрёл бы вид
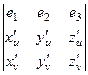 . Этот способ тоже употребляется на практике. Так, например, задать сферу можно с помощью двух параметров, аналогичных широте и долготе на земном шаре. Тогда в формуле площади поверхности под корнем - сумма квадратов трёх миноров, состоящих из частных производных, расположенных в двух нижних строках определителя.
. Этот способ тоже употребляется на практике. Так, например, задать сферу можно с помощью двух параметров, аналогичных широте и долготе на земном шаре. Тогда в формуле площади поверхности под корнем - сумма квадратов трёх миноров, состоящих из частных производных, расположенных в двух нижних строках определителя.
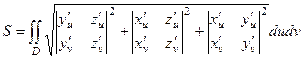 .
.
Теперь представим следующую ситуацию: проволока или поверхность имеют переменную плотность, и требуется найти массу. Если плотность единичная, то фактически найти длину кривой (или площадь поверхности) это и означает найти данную массу. Но если плотность переменная, то при мелком разбиении нужно на каждом участке надо умножать длину (площадь) соответствующего участка на плотность. Именно такая задача привела к появлению понятий криволинейного и поверхностного интегралов 1-го рода (от скалярных функций).
Определение. Пусть дана некоторая кривая в пространстве 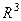 . Во всех точках пространства (и в частности, на кривой) задана ограниченная и непрерывная скалярная функция
. Во всех точках пространства (и в частности, на кривой) задана ограниченная и непрерывная скалярная функция 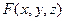 . Введём разбиение кривой на n частей, длину каждой из них обозначим
. Введём разбиение кривой на n частей, длину каждой из них обозначим 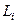 . Возьмём на каждой из этих частей по одной точке
. Возьмём на каждой из этих частей по одной точке 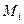 . Рассмотрим такую сумму:
. Рассмотрим такую сумму: 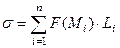 (она называется интегральной суммой). Предел таких сумм при
(она называется интегральной суммой). Предел таких сумм при 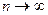 называется криволинейным интегралом 1-го рода (от скалярной функции).
называется криволинейным интегралом 1-го рода (от скалярной функции).
Примечание. 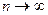 следует рассматривать при условии, что разбиение измельчается по всей кривой, т.е.
следует рассматривать при условии, что разбиение измельчается по всей кривой, т.е. 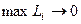 .
.
Формулы вычисления криволинейного интеграла 1-го рода.
Обозначение: 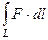 .
.
1) Для параметрически заданной кривой в трёхмерном пространстве: 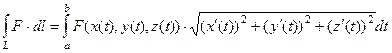 .
.
2) Для параметрически заданной кривой в плоскости: 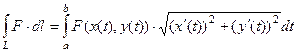 .
.
На практике это значит, что необходимо все переменные 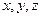 в составе функции
в составе функции 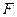 выразить через параметр
выразить через параметр 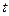 , таким образом, функция станет зависеть только одной переменной, получим
, таким образом, функция станет зависеть только одной переменной, получим 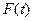 , и далее сводится к обычному определённому интегралу от
, и далее сводится к обычному определённому интегралу от 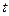 .
.
3) Для явно заданной кривой в плоскости: 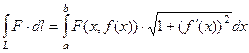 .
.
Примечание. Если 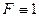 , то из этих получаются прежние формулы длины кривой, указанные в начале лекции.
, то из этих получаются прежние формулы длины кривой, указанные в начале лекции.
Пример. Найти массу проволоки, расположенной в виде полуокружности в верхней полуплоскости, если плотность равна 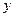 .
.
Решение. Так как все точки расположены на окружности, то лучше задать параметрически: 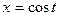 ,
, 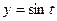 , причём
, причём 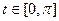 .
.
Далее, 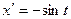 ,
, 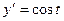 .
.
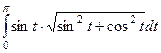 =
= 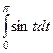 =
= 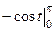 =
= 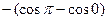 = 2.
= 2.
Определение. Пусть дана некоторая поверхность в пространстве 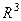 . Во всех точках пространства (и в частности, на поверхности) задана ограниченная и непрерывная скалярная функция
. Во всех точках пространства (и в частности, на поверхности) задана ограниченная и непрерывная скалярная функция 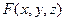 . Введём разбиение поверхности на n частей двумя семействами линий, площадь каждой части обозначим
. Введём разбиение поверхности на n частей двумя семействами линий, площадь каждой части обозначим 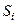 . Возьмём на каждой из этих частей по одной точке
. Возьмём на каждой из этих частей по одной точке 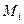 . Рассмотрим интегральную сумму:
. Рассмотрим интегральную сумму: 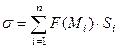 . Предел таких сумм при
. Предел таких сумм при 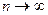 называется поверхностным интегралом 1-го рода (от скалярной функции).
называется поверхностным интегралом 1-го рода (от скалярной функции).
Обозначение 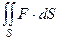
Формулы вычисления поверхностного интеграла 1-го рода.
Для явно заданной поверхности:
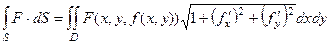 .
.
Для параметрически заданной поверхности правая часть формулы была бы такого вида:
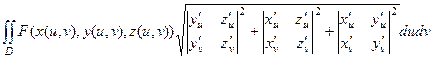
Мы на практике будем, как правило, стараться сводить к явному виду.
Ещё один физический смысл. 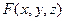 этот вовсе не обязательно плотность какой-то тонкой пластины. Допустим, что
этот вовсе не обязательно плотность какой-то тонкой пластины. Допустим, что 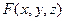 - уровень радиации, заданный во всех точках пространства. То есть, эта функция может быть задана во всем пространстве, независимо от наличия или отсутствия какой-либо поверхности. Если затем расположить там поверхность, то поверхностный интеграл 1 рода будет показывать, какую суммарную дозу радиоактивности получит эта поверхность.
- уровень радиации, заданный во всех точках пространства. То есть, эта функция может быть задана во всем пространстве, независимо от наличия или отсутствия какой-либо поверхности. Если затем расположить там поверхность, то поверхностный интеграл 1 рода будет показывать, какую суммарную дозу радиоактивности получит эта поверхность.
Пример. Дана функция 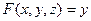 . Пусть поверхность - верхняя полусфера радиуса 1. Найти поверхностный интеграл 1 рода.
. Пусть поверхность - верхняя полусфера радиуса 1. Найти поверхностный интеграл 1 рода.
Решение. Верхняя полусфера задаётся в явной форме так:
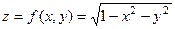 . Частные производные:
. Частные производные:
 ,
, 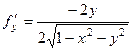 .
.
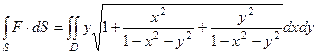 =
=
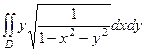 , где
, где 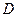 - проекция полусферы на горизонтальную плоскость, то есть круг радиуса 1, а поскольку круг, то выгодно будет перейти к полярным координатам.
- проекция полусферы на горизонтальную плоскость, то есть круг радиуса 1, а поскольку круг, то выгодно будет перейти к полярным координатам.
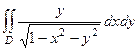 =
= 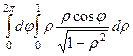 =
= 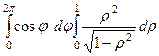 =
=
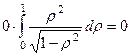 . К счастью, интеграл по
. К счастью, интеграл по  здесь даже не пришлось считать, т.к. интеграл по
здесь даже не пришлось считать, т.к. интеграл по  выделяется отдельным множителем и он равен 0.
выделяется отдельным множителем и он равен 0.
Дата: 2018-12-21, просмотров: 350.