Приходовский М.А.
Математика
Курс лекций
Семестр 3
Учебное пособие
Для специальности
Информатика и вычислительная техника»
Томск
ТУСУР
2018
Электронное учебное пособие составлено и скорректировано с учётом реального проведения лекций на ФСУ в группах 437-1,2,3 осенью 2018 года.
(ДОК №) - доказательства формул или теорем, которые попадают в теооретические билеты.
Оглавление
| Глава 1. Криволинейные и поверхностные интегралы, теория поля...................................................................................... § 1. Криволинейные и поверхностные интегралы 1 рода............ § 2. Криволинейные и поверхностные интегралы 2 рода............ § 3. Элементы теории поля.............................................................. Глава 2. Теория функций комплексного переменного ........... § 1. Действия с комплексными числами......................................... § 2. Функции комплексного переменного...................................... § 3. Дифференцирование комплексных функций......................... § 4. Интегрирование комплексных функций................................. § 5. Интегральная формула Коши .................................................. § 6. Комплексные числа и дифференциальные уравнения.......... § 7. Гиперкомплексные числовые системы. Кватернионы......... Глава 3. Особые точки и вычеты ............................................. § 1. Нули аналитической функции............................................... § 2. Особые точки .......................................................................... § 3. Вычеты..................................................................................... § 4. Приложения вычетов.............................................................. Глава 4. Ряды Фурье .................................................................... | 5 5 10 17 33 33 35 41 50 58 70 71 76 76 77 84 |
Оглавление по номерам лекций
| Лекция 1.......................................................................................... Лекция 2.......................................................................................... Лекция 3.......................................................................................... Лекция 4.......................................................................................... Лекция 5.......................................................................................... Лекция 6.......................................................................................... Лекция 7.......................................................................................... Лекция 8.......................................................................................... Лекция 9.......................................................................................... Лекция 10......................................................................................... Лекция 11......................................................................................... Лекция 12......................................................................................... Лекция 13......................................................................................... Лекция 14......................................................................................... Лекция 15......................................................................................... Лекция 16......................................................................................... | 5 13 21 32 41 50 58 69 77 86 |
ЛЕКЦИЯ 1. 05.09.2018
Глава 1.
Криволинейные и поверхностные интегралы, теория поля
ЛЕКЦИЯ 2. 12.09.2018
Пример вычисления поверхностного интеграла 2 рода
Векторное поле 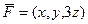 , поверхность - эллиптический параболоид
, поверхность - эллиптический параболоид 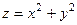 , где
, где  .
.
Решение. Вектор нормали 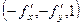 в данном случае
в данном случае 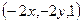 .
.
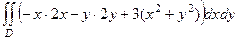 =
=  .
.
где D - проекция этой части параболоида на плоскость Оху, это круг радиуса 1. Перейдём к полярным координатам.
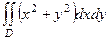 =
= 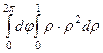 =
=  =
=  .
.
Далее рассмотрим взаимосвязь между двойным интегралом по плоской области и криволинейным интегралом по её границе (формула Грина). Вам давно известна формула Ньютона-Лейбница, выражающая взаимосвязь между интегралом по отрезку и значениями первообразной на его границе (граница состоит из 2 точек). Но подобные взаимосвязи есть также и и между плоской областью и её границей.
Определение. Работа векторного поля по перемещению точки по замкнутой кривой называется циркуляцией.
Обозначение:  или
или 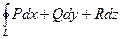 .
.
Для плоского векторного поля  верна такая формула. Формула Грина:
верна такая формула. Формула Грина: 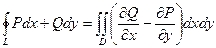 .
.
Работа силы по границе области равна двойному интегралу от 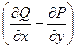 по этой плоской области.
по этой плоской области.
Доказательство (ДОК 2). Спроецируем область на ось Ох, обозначим границы проекции: точки  . Сама граница области тогда условно подразделяется на две линии, снизу
. Сама граница области тогда условно подразделяется на две линии, снизу  , а сверху
, а сверху 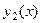 . Чтобы движение по замкнутому контуру происходило против часовой стрелки, надо по
. Чтобы движение по замкнутому контуру происходило против часовой стрелки, надо по 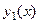 двигаться слева направо, а по
двигаться слева направо, а по 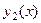 справа налево.
справа налево.
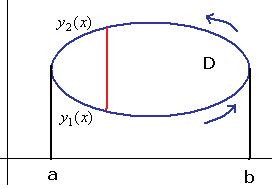
Рассмотрим подробнее интеграл от функции 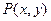 по границе области. В соответствии со всем сказанным, он может быть записан так:
по границе области. В соответствии со всем сказанным, он может быть записан так: 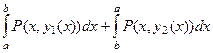 . Но во втором интеграле можно изменить
. Но во втором интеграле можно изменить 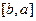 на
на 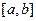 , сменив знак.
, сменив знак.
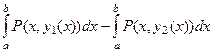 и их можно объединить
и их можно объединить
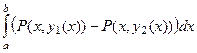 =
= 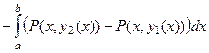
разность, которая внутри интеграла, является результатом применения формулы Ньютона-Лейбница по переменной 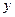 :
:
запишем это в виде: 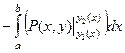 .
.
Но если формула Ньютона-Лейбница применяется к  , значит,
, значит,  это первообразная по
это первообразная по  , а она очевидно, является первообразной от своей производной
, а она очевидно, является первообразной от своей производной 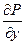 . То есть:
. То есть:
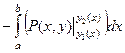 =
= 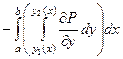 а этой как раз и есть двойной интеграл по области D.
а этой как раз и есть двойной интеграл по области D.
 =
= 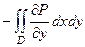 .
.
Аналогично можно спроецировать область D на ось Оу, допустим проекция займёт некоторый отрезок 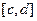 . Левую и правую линии, составляющие замкнутый контур, обозначим
. Левую и правую линии, составляющие замкнутый контур, обозначим  и
и 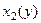 . Правая здесь будет
. Правая здесь будет 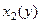 (она дальше от оси Оу).
(она дальше от оси Оу).
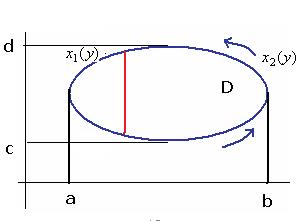
Тогда 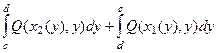 =
= 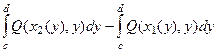 =
= 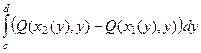 =
=
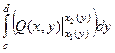 =
=  =
= 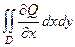 .
.
Сложим два полученных равенства и получается двойной интеграл
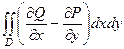 .
.
Пример вычисления работы по единичной окружности от поля
 без формулы Грина и по формуле Грина.
без формулы Грина и по формуле Грина.
Способ 1. Параметрически: 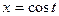 ,
,  ,
, 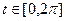 .
.
При этом 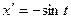 ,
, 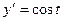 .
.
 =
= 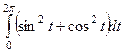 =
= 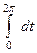 =
= 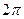 .
.
Способ 2.  . Тогда
. Тогда 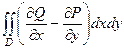 =
= 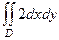 =
= 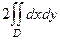 где D - круг радиуса 1. Тогда интеграл от 1 это его площадь.
где D - круг радиуса 1. Тогда интеграл от 1 это его площадь. 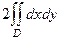 =
= 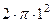 =
= 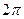 .
.
Элементы теории поля
Скалярное поле, или скалярная функция: 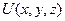 .
.
Векторная функция, которая отображает  называется векторным полем.
называется векторным полем.
Заметим, что градиент скалярной функции - это векторная функция:
 ,
,  ,
, 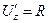
То есть, по скалярному полю всегда можно построить некоторое векторное.
Пример: 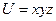 . Тогда
. Тогда 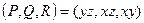 .
.
А вот обратная задача: если даны некоторые 3 скалярные функции, т.е. векторное поле, всегда ли они являются частными производными какой-то единой скалярной функции? Оказывается, нет.
Определение. Если существует такая скалярная функция 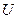 , что выполняется
, что выполняется  ,
, 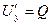 ,
, 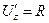 , (то есть их общая первообразная), то векторное поле называется потенциальным, а функция
, (то есть их общая первообразная), то векторное поле называется потенциальным, а функция 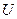 называется потенциалом поля
называется потенциалом поля 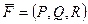 .
.
Свойство. Если 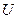 - потенциал, то
- потенциал, то 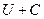 - тоже потенциал.
- тоже потенциал.
Доказательство: 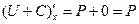 ,
, 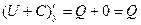 ,
, 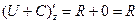 .
.
Потенциал определяется с точностью до константы (точно так же как и первообразная). Именно поэтому в физике важна именно разность потенциалов, а не сам потенциал.
Примеры.
Пример не потенциального поля.
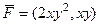 . Первообразная от 1 компоненты по
. Первообразная от 1 компоненты по 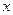 это
это 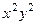 , однако первообразная по
, однако первообразная по 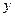 от второй компоненты совсем другая:
от второй компоненты совсем другая:
 , они не совпадают.
, они не совпадают.
Пример потенциального поля.
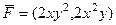 . Его потенциал:
. Его потенциал: 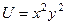 .
.
Далее нам надо научиться выяснять 2 вопроса:
1) выяснять, является ли поле потенциальным.
2) вычислять потенциал, если оно потенциально.
Теорема 1. Криволинейный интеграл 2 рода не зависит от пути 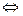 циркуляция по замкнутому контуру равна 0.
циркуляция по замкнутому контуру равна 0.
Доказательство (ДОК 3).

Необходимость. Пусть интеграл зависит только от начальной и конечной точки, и не зависит от пути, соединяющего точки А,В. Возьмём какой-нибудь замкнутый контур, разобьём его какими-нибудь случайно взятыми точками. Докажем, что циркуляция равна 0.
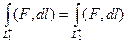
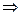

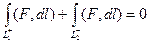 . Но так как объединение 2 частей в замкнутый контур это
. Но так как объединение 2 частей в замкнутый контур это  , то получается:
, то получается: 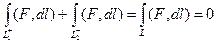 .
.
Достаточность.
Пусть для любого замкнутого контура 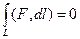 . Если даны какие-то точки А,В, и какие-то две различные линии, соединяющие их, то эти две линии можно объединить в единый замкнутый контур.
. Если даны какие-то точки А,В, и какие-то две различные линии, соединяющие их, то эти две линии можно объединить в единый замкнутый контур.
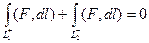
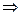

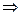
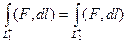 ,
,
что и требовалось доказать.
Теорема 2. Поле F потенциально 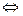 криволинейный интеграл 2 рода от F не зависит от пути, причём тогда потенциал в любой точке
криволинейный интеграл 2 рода от F не зависит от пути, причём тогда потенциал в любой точке 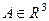 вычисляется в виде
вычисляется в виде 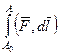 где A0 - некоторая начальная точка, как правило (0,0,0).
где A0 - некоторая начальная точка, как правило (0,0,0).
Доказательство (ДОК 4).
Необходимость. Если поле потенциально то  ,
,  ,
, 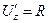
а тогда в интеграле 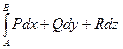 получится
получится 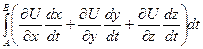 а по формуле полного дифференциала это
а по формуле полного дифференциала это  но ведь первообразная от производной - это сама функция U, тогда работа поля
но ведь первообразная от производной - это сама функция U, тогда работа поля 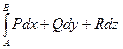 в итоге равна
в итоге равна 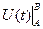 =
= 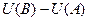 то есть зависит только от начальной и конечной точки.
то есть зависит только от начальной и конечной точки.
Достаточность.
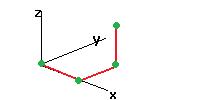
Если криволинейный интеграл для поля (P,Q,R) не зависит от пути, возьмём начальную точку, например начало координат (0,0,0). Введём некоторую скалярную функцию U(x,y,z) равную работе поля от (0,0,0) до точки А(x,y,z). То есть  .
.
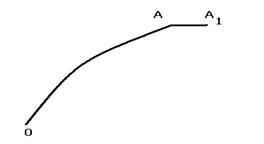
А теперь мы докажем, что именно эта функция является потенциалом.
Составим путь из дуги от 0 до А и дополнительного маленького горизонтального отрезка вдоль оси Ох. Интеграл от 0 до А равен U(А). Интеграл от 0 до А1 равен U(А1).
Координаты точек: А (x,y,z) и А1 (x+∆x,y,z) .
Тогда 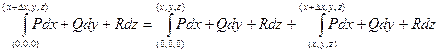 =
= 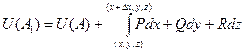 но в интеграле по отрезку АА1 меняется только x, при этом y, z константы, то есть dy = 0, dz = 0.
но в интеграле по отрезку АА1 меняется только x, при этом y, z константы, то есть dy = 0, dz = 0.
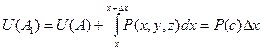 для некоторой промежуточной точки с, где достигается среднее значение.
для некоторой промежуточной точки с, где достигается среднее значение.
Тогда  , следовательно,
, следовательно, 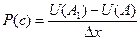 =
= 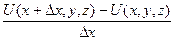 .
.
Но точка с тоже стремится к х при ∆x →0.
То есть 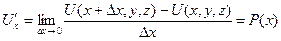 . Итак,
. Итак,  .
.
Аналогично, рассматривая точку А1 с координатами А1 (x,y+∆y,z) получили бы 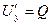 , а если то А1 (x,y,z+∆z) то
, а если то А1 (x,y,z+∆z) то 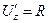 . Итак, поле потенциально и U(x,y,z), равная работе силы по перемещению от начальной точки до (x,y,z), является потенциалом.
. Итак, поле потенциально и U(x,y,z), равная работе силы по перемещению от начальной точки до (x,y,z), является потенциалом.
Следствие. Поле F потенциально 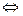 циркуляция по замкнутому контуру равна 0.
циркуляция по замкнутому контуру равна 0.
ЛЕКЦИЯ 3. 19.09.2018
Итак, в конце прошлой лекции мы доказали, что поле потенциально 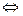 криволинейный интеграл 2 рода не зависит от пути. Этот критерий позволяет вычислить потенциал, если известно, что поле потенциально, однако практически ничем не поможет выяснить изначально вопрос о том, потенциально ли поле. Ведь кривых, соединяющих две точки А,В бесконечно много, и невозможно вычислить интегралы по всем этим кривым. Поэтому для проверки потенциальности необходим другой критерий.
криволинейный интеграл 2 рода не зависит от пути. Этот критерий позволяет вычислить потенциал, если известно, что поле потенциально, однако практически ничем не поможет выяснить изначально вопрос о том, потенциально ли поле. Ведь кривых, соединяющих две точки А,В бесконечно много, и невозможно вычислить интегралы по всем этим кривым. Поэтому для проверки потенциальности необходим другой критерий.
Теорема 3. 1) Если поле 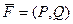 потенциально то симметрична производная матрица
потенциально то симметрична производная матрица 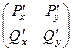 .
.
2) Если граница области D, в которой задано векторное поле, является односвязным множеством, и симметрична производная матрица 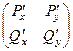 , то поле потенциально.
, то поле потенциально.
Доказательство (ДОК 5).
1) Необходимость. Пусть поле потенциально. Тогда 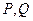 являются производными от какой-то общей функции
являются производными от какой-то общей функции 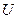 , т.е.
, т.е.  ,
,  . тогда
. тогда 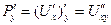 ,
, 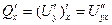 . Но смешанные частные производные 2-го порядка совпадают, значит,
. Но смешанные частные производные 2-го порядка совпадают, значит, 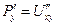 =
= 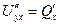 .
.
а следовательно, 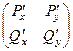 =
=  .
.
2) Достаточность. Сначала подробнее о том, почему односвязной должна быть даже не сама область, а её граница. Это означает, что внутри плоской области нет пустот, то есть областей, не принадлежащих данному множеству, то есть каждый контур можно стянуть в точку. Например, кольцо само как плоское множество является односвязным множеством, любую пару точек можно соединить какой-либо кривой. Но его граница не является односвязной, а состоит из двух окружностей, и не всякую пару точек на границе можно соединить кривой, лежащей на границе. Например, если А,В на внешней и внутреннней окружности, то соединяющая кривая проходит не только по границе:
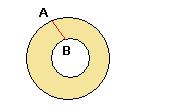
Здесь мы будем использовать формулу Грина, которую доказали ранее, а там фактически неявно это и предполагали при записи двойного интеграла, когда для  рассматривался отрезок
рассматривался отрезок 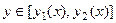 , то есть такая ситуация, как для кольца, не рассматривается, а только множества без внутренних пустот.
, то есть такая ситуация, как для кольца, не рассматривается, а только множества без внутренних пустот.
Если производная матрица симметрична, то 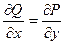 (в других обозначениях
(в других обозначениях 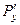 =
=  ). Тогда
). Тогда 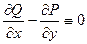 , и двойной интеграл по любой плоской области равен 0:
, и двойной интеграл по любой плоской области равен 0: 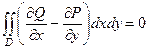 .
.
Но ведь тогда для любого замкнутого контура получается, что по формуле Грина, если двойной интеграл по его внутренней области 0, то и циркуляция по границе тоже 0:
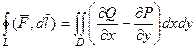 = 0,
= 0,
а если для любого контура циркуляция 0, то поле потенциально, что следует из теорем 1 и 2, доказанных ранее.
В 3-мерном случае требуется совпадение трёх пар производных, доказательство показано пока для 2-мерного случая, чтобы использовать формулу Грина. В 3-мерном случае будет использоваться формула Стокса, которую введём чуть позже.
Алгоритм нахождения потенциала.
1. Выяснить потенциальность поля, проверив симметричность производной матрицы (она сотоит из всех частных производных: от всех компонент векторного поля по всем переменным).
2. Найти потенциал, как скалярную функцию, равную криволинейному интегралу от фиксированной точки до произвольной.
Как правило, в качестве «начальной» фиксированной точки рассматривают начало координат, если же в функциях присутствуют к примеру 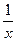 или
или 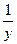 , то можно взять в качестве начальной точку (1,1) а не (0,0).
, то можно взять в качестве начальной точку (1,1) а не (0,0).
Путь от начальной точки до может быть по любой кривой, но практически лучше по ломаной, состоящей из отрезков, параллельных осям координат. Сначала от (0,0) к (x,0) а затем 2-е звено до точки (x,y).
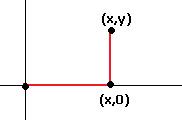
Пример. Доказать, что поле 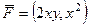 потенциально и найти потенциал.
потенциально и найти потенциал.
Решение. Шаг 1. Сначала найдём производную матрицу, вычислив все частные производные по всем переменным:
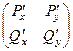 =
= 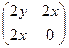 . Мы видим, что она симметрична. Значит, поле потенциально.
. Мы видим, что она симметрична. Значит, поле потенциально.
Шаг 2. Найдём криволинейный интеграл от (0,0) до 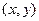 , соединив с помощью ломаной. Лучше всего даже обозначить конечную точку
, соединив с помощью ломаной. Лучше всего даже обозначить конечную точку 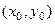 , чтобы не путать обозначение переменной, по которой ведётся интегрирование, и верхнего предела. Вычислив
, чтобы не путать обозначение переменной, по которой ведётся интегрирование, и верхнего предела. Вычислив 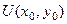 , затем мы учтём тот факт, что эта точка была произвольной, и сможем записать уже просто
, затем мы учтём тот факт, что эта точка была произвольной, и сможем записать уже просто 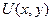 .
.
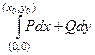 разбивается на сумму двух интегралов, по каждому участку ломаной, причём на каждом из них обнуляется один из двух дифференциалов: на горизонтальном отрезке меняется только
разбивается на сумму двух интегралов, по каждому участку ломаной, причём на каждом из них обнуляется один из двух дифференциалов: на горизонтальном отрезке меняется только  , а тогда
, а тогда 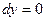 , на вертикальном меняется
, на вертикальном меняется 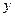 , тогда
, тогда 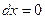 .
.
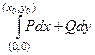 =
= 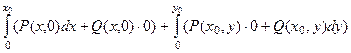
в обоих интегралах формально присутствуют оба слагаемых, но одно из них обнуляется, поэтому выглядит далее так, как будто распределилось по одному слагаемому в каждый интеграл.
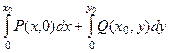 в первом фиксировано
в первом фиксировано 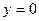 , а на втором участке переменная
, а на втором участке переменная  уже достигла
уже достигла  и далее не меняется, поэтому там
и далее не меняется, поэтому там 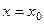 .
.
Для данного конкретного примера получается
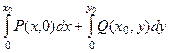 =
= 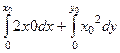 =
= 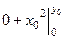 =
= 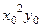 .
.
Итак, 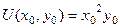 , тогда можно сказать, что
, тогда можно сказать, что 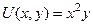 .
.
Проверка. 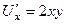 ,
, 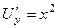 .
.
Определение. Дивергенция векторного поля.
 (сумма элементов главной диагонали производной матрицы). Это скалярная величина.
(сумма элементов главной диагонали производной матрицы). Это скалярная величина.
Определение. Ротор векторного поля.
rot(F) = 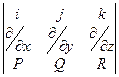 =
= 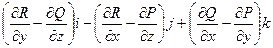
в других обозначениях это выглядит так: 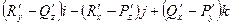 .
.
Таким образом, ротор - это некоторое новое векторное поле из 3 компонент, построенное с помощью исходного векторного поля.
Определение. Если ротор = 0 то поле называется безвихревым.
Обратим внимание, что при определении дивергенции используются 3 частных производных, которые расположены в производной матрице по диагонали: дифференцируется i-я компонента по i-й переменной, а при определении ротора - только производные компонент по «чужим» номерам переменных, таких 6 из 9 в производной матрице:

Причём, 3-я координата ротора это та разность, которая уже использовалась в формуле Грина. Если поле плоское, а именно 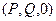 , то отлична от 0 только лишь третья компонента, а именно та, которая была в формуле Грина.
, то отлична от 0 только лишь третья компонента, а именно та, которая была в формуле Грина.
Пример, демонстрирующий геометрический смысл ротора.
Рассмотрим векторное поле 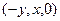 .
.
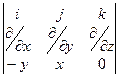 =
=  .
.
т.е. если векторы в плоскости соответствуют вращению против часовой стрелки, то ротор направлен вверх.
Пусть две из трёх компонент векторного поля равны 0. Например, 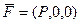 или
или  или
или 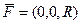 . Тогда все векторы направлены в одну сторону. Например, рассмотрим
. Тогда все векторы направлены в одну сторону. Например, рассмотрим  . Тогда векторное поле выглядит примерно так:
. Тогда векторное поле выглядит примерно так:
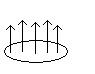
То есть, фактически здесь информацию содержит только скалярная функция 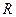 , все векторы направлены по одной линии и отличаются лишь длиной. Тогда поток поля через поверхность можно вычислить через двойной интеграл
, все векторы направлены по одной линии и отличаются лишь длиной. Тогда поток поля через поверхность можно вычислить через двойной интеграл 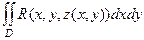 , где D это проекция поверхности на плоскость 0xy, ведь в формуле:
, где D это проекция поверхности на плоскость 0xy, ведь в формуле: 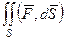 =
= 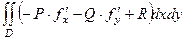
компоненты 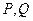 равны 0. Аналогично, если есть только одна ненулевая компонента
равны 0. Аналогично, если есть только одна ненулевая компонента 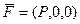 то получится
то получится 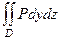 , а если
, а если 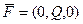 то
то 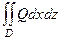 . Но ведь любой вектор в пространстве можно представить в виде суммы трёх векторов, параллельных осям. Таким образом, и векторное поле можно разложить на сумму 3 компонент, а именно
. Но ведь любой вектор в пространстве можно представить в виде суммы трёх векторов, параллельных осям. Таким образом, и векторное поле можно разложить на сумму 3 компонент, а именно 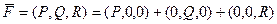 . Тогда поверхностный интеграл 2 рода можно вычислить с помощью суммы трёх двойных интегралов по трём проекциям на координатные плоскости соответственно, т.е. верна ещё и такая формула:
. Тогда поверхностный интеграл 2 рода можно вычислить с помощью суммы трёх двойных интегралов по трём проекциям на координатные плоскости соответственно, т.е. верна ещё и такая формула:
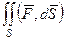 =
= 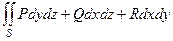 (*)
(*)
Пусть теперь L - замкнутая пространственная кривая, S - поверхность, натянутая на эту кривую, т.е. кривая является краем поверхности, для наглядности представьте например, окружность и полусферу, то есть, S не обязано лежать в плоскости. Да впрочем, и сам замкнутый контур L тоже не обязан лежать в плоскости. Так, например, гнутое железное колесо является хоть и замкнутой, но не плоской кривой. Циркуляция по контуру L выражается через поверхностный интеграл по S, а именно, равна потоку ротора через S. Эта взаимосвязь выражена в формуле Стокса, которая является обобщением формулы Грина на пространственный случай.
Формула Стокса. 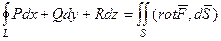 .
.
Кратко рассмотрим идею доказательства формулы Стокса. Надо рассмотреть 3 проекции на координатные плоскости. При подробной записи формулы Стокса, если расшифровать подробно все 3 координаты ротора и кроме того, применить при этом формулу (*) выведенную чуть выше, получим:
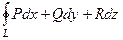 =
=
= 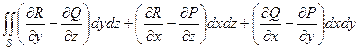 .
.
Обратим внимание, что 3-е слагаемое в точности такое, как в формуле Грина. Если рассмотреть проекция векторного поля на координатную плоскость 0xy, а именно для поля 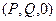 , доказательство в точности такое, как было для формулы Грина, что приведёт к слагаемому
, доказательство в точности такое, как было для формулы Грина, что приведёт к слагаемому
 . Если то же самое сделать в двух других координатных плоскостях, 0xz и 0yz, то получим два других слагаемых.
. Если то же самое сделать в двух других координатных плоскостях, 0xz и 0yz, то получим два других слагаемых.
Из формулы Стокса следует, что и в 3-мерном случае потенциальность векторного поля эквивалентна симметричности производной матрицы:
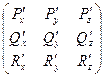
Действительно, если 3 пары частных производных совпадают:  то ротор равен 0, а значит и поток ротора равен 0, но тогда по формуле Стокса и циркуляция равна 0, из чего следует потенциальность поля (чуть раньше это было выведено из формулы Грина для 2-мерного поля). Итак, эквивалентны такие 3 условия:
то ротор равен 0, а значит и поток ротора равен 0, но тогда по формуле Стокса и циркуляция равна 0, из чего следует потенциальность поля (чуть раньше это было выведено из формулы Грина для 2-мерного поля). Итак, эквивалентны такие 3 условия:
Симметрична производная матрица 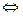

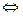 поле потенциально.
поле потенциально.
Пример. Доказать, что поле 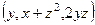 потенциально и найти потенциал.
потенциально и найти потенциал.
Решение.
Сначала найдём матрицу из всех 9 частных производных.
 =
=  . Матрица симметрична, это в то же самое время означает, что ротор равен 0. Поле потенциально.
. Матрица симметрична, это в то же самое время означает, что ротор равен 0. Поле потенциально.
Вычислим криволинейный интеграл по ломаной,соединяющей точки 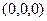 и
и 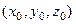 .
.
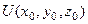 =
= 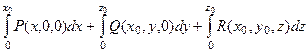 =
= 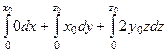 =
= 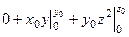 =
= 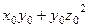 .
.
Тогда 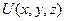 =
=  .
.
Проверка:
 =
= 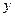 ,
,  =
= 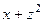 ,
, 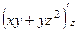 =
= 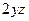 .
.
Рассмотрим ещё одну разновидность формул, взаимосвязывающих интеграл по границе и внутренней части области.
ЛЕКЦИЯ 4. 26.09.2018
Глава 2.
Доказательство (ДОК 9).
Обобщение любой функции на случай комплексного переменного можно проводить с помощью рядов. Поскольку существует любая степень мнимой единицы 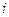 , например
, например 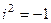 ,
, 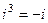 ,
, 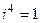 , и т.д. то этот подход возможен. Вспомним разложение экспоненты в ряд Тейлора.
, и т.д. то этот подход возможен. Вспомним разложение экспоненты в ряд Тейлора. 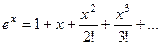
Тогда вычислим 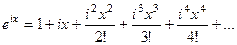 =
=
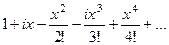 теперь соберём в отдельные слагаемые все части, где нет
теперь соберём в отдельные слагаемые все части, где нет 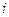 , и где есть
, и где есть 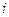 .
.
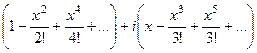 но ведь в 1 и 2 скобках стоят разложения
но ведь в 1 и 2 скобках стоят разложения 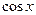 и
и 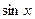 . Итак,
. Итак, 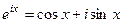 , что и требовалось доказать.
, что и требовалось доказать.
Теперь для любого числа 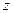 можно вычислить
можно вычислить  :
:
 =
= 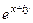 =
= 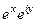 =
= 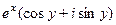 =
=  .
.
Для сопряжённого числа можно вычислить аналогично:
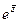 =
= 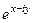 =
=  =
= 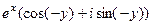 =
= 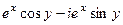 .
.
(здесь воспользовались чётностью cos и нечётностью sin).
Получается, сопряжение под знаком экспоненты приводит
Доказательство (ДОК 10).
Рассмотрим для действительного числа 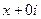 и покажем, что данные функции, а именно
и покажем, что данные функции, а именно 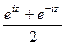 и
и 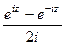 , приведут именно к обычному синусу и косинусу действительного числа, т.е. они обобщают синус и косинус.
, приведут именно к обычному синусу и косинусу действительного числа, т.е. они обобщают синус и косинус.
1) 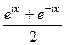 =
= 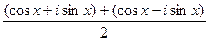 =
= 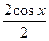 =
= 
2) 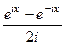 =
= 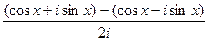 =
= 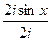 =
= 
Неограниченность синуса и косинуса в комплексной плоскости.
Пример. 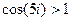 .
.
Вычислим: 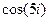 =
= 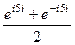 =
= 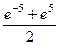
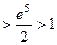 .
.
Логарифм комплексного числа.
Обобщённый логарифм вводится с помощью формулы:
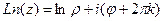 .
.
Доказательство (ДОК 11).
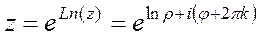
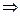
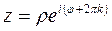
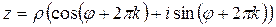 ,
,
это означает 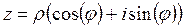 так как синус и косинус не зависят от прибавления угла, кратного
так как синус и косинус не зависят от прибавления угла, кратного 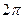 . Это равенство уже очевидно, так как это и есть тригонометрическая форма комплексного числа.
. Это равенство уже очевидно, так как это и есть тригонометрическая форма комплексного числа.
Если вычислять логарифм положительного действительного числа, то 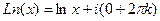 , т.е. одна точка из бесконечного множества попадает на действительную ось, потому что исходный угол
, т.е. одна точка из бесконечного множества попадает на действительную ось, потому что исходный угол 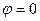 . Для любого числа, которое не является действительным положительным,
. Для любого числа, которое не является действительным положительным,  , поэтому происходит сдвиг этой последовательности на часть деления, и ни одна точка не попадёт на действительную ось.
, поэтому происходит сдвиг этой последовательности на часть деления, и ни одна точка не попадёт на действительную ось.
Пример. Вычислить  .
.
Здесь 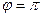 ,
, 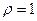 . Поэтому
. Поэтому 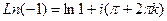 =
=  .
.
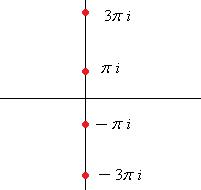
Точки в комплексной плоскости: 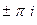 ,
, 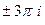 ,
, 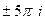 , и так далее.
, и так далее.
Ни одного значения на действительной оси нет, и здесь, по сравнению со значениями логарифма положительного числа, сдвиг на половину деления: одна точка ушла вверх с действительной оси, а другая ещё не достигла этой оси. Чертёж:
Пример. Вычислить 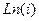 .
.
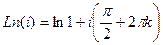 =
= 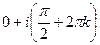 . Последовательность значений такова:
. Последовательность значений такова: 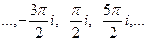 каждая соседняя пара отличается на
каждая соседняя пара отличается на 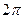 по высоте. Здесь сдвиг вверх всего на четверть деления, а не на половину, как для
по высоте. Здесь сдвиг вверх всего на четверть деления, а не на половину, как для  .
.
1) При фиксированном модуле исходного числа и увеличении его аргумента, эта последовательность точек плывёт вверх, при полном повороте на 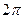 как раз следующая точка попадёт на место предыдущей.
как раз следующая точка попадёт на место предыдущей.
2) При фиксированном аргументе исходного числа и увеличении его модуля, эта последовательность точек плывёт вправо, если исходная точка внутри единичной окружности то множество значений логарифма в левой полуплоскости, так как 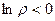 , а если вне единичной окружности, то в правой полуплоскости.
, а если вне единичной окружности, то в правой полуплоскости.
Динамическая анимация, показывающая поведение значений  в зависимости от колебаний модуля или аргумента
в зависимости от колебаний модуля или аргумента  , показана в следующем обучающем видеоролике:
, показана в следующем обучающем видеоролике:
http://www.youtube.com/watch?v=LKFFn-TSLd0
Замечание. Единственная точка в комплексной плоскости, для которой не существует логарифма, это 0. Ведь в этом случае 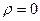 , и не существует
, и не существует  .
.
Пример. Вычислим 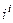 .
.
Решение. Представим 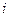 , расположенную в основании, в виде
, расположенную в основании, в виде  . Тогда
. Тогда 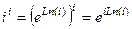 , причём чуть выше мы вычисляли
, причём чуть выше мы вычисляли
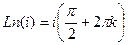 . Тогда
. Тогда 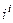 =
= 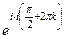 =
= 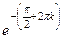 т.е. получается бесконечное множество точек на действительной оси.
т.е. получается бесконечное множество точек на действительной оси.
Для всякой функции 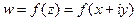 можно отдельно выделить действительную и мнимую части, и представить в виде
можно отдельно выделить действительную и мнимую части, и представить в виде
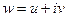 . Таким образом, возникают понятия: действительная и мнимая часть функции, обозначения:
. Таким образом, возникают понятия: действительная и мнимая часть функции, обозначения:  ,
,  . Итак, комплексной функции можно поставить в соответствие некоторое отображение из
. Итак, комплексной функции можно поставить в соответствие некоторое отображение из 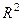 в
в 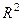 , а именно
, а именно  . Но график такого отображения был бы в 4-мерном пространстве, поэтому изобразить его в нашем 3-мерном пространстве невозможно. Но мы можем пользоваться неким подобием графика, а именно, рассматривать чертёж искажений плоскости, изучать, в какие линии отображаются горизонтальные либо вертикальные линии из исходной плоскости.
. Но график такого отображения был бы в 4-мерном пространстве, поэтому изобразить его в нашем 3-мерном пространстве невозможно. Но мы можем пользоваться неким подобием графика, а именно, рассматривать чертёж искажений плоскости, изучать, в какие линии отображаются горизонтальные либо вертикальные линии из исходной плоскости.
Пример. Разложить 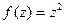 на действительную и мнимую часть, изобразить искажения плоскости при переходе
на действительную и мнимую часть, изобразить искажения плоскости при переходе 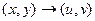 .
.
1) 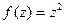 =
= 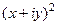 =
= 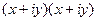 =
=  .
.
Таким образом, 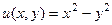 ,
,  .
.
Чтобы исследовать, куда переходят горизонтальные прямые, зафиксируем  , при этом
, при этом 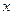 изменяется от
изменяется от 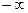 до
до 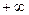 , пусть движение задано с помощью параметра
, пусть движение задано с помощью параметра 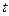 :
:
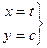
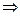
 .
.
Чтобы составить уравнение, взаимосвязывающее  , и узнать, какая это кривая, исключим параметр
, и узнать, какая это кривая, исключим параметр 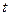 , выразив из второго уравнения:
, выразив из второго уравнения:  , тогда
, тогда 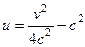 . Это парабола, лежащая на боку, ветвями направленная вправо, причём чем больше
. Это парабола, лежащая на боку, ветвями направленная вправо, причём чем больше 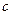 , тем левее вершина, и тем более пологая парабола получается, ведь
, тем левее вершина, и тем более пологая парабола получается, ведь 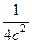 при этом меньше. А если
при этом меньше. А если 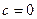 , то возникает предельный случай: обе ветви смыкаются в одну линию и образуют правую полуось. Действительная ось отображается на правую полуось в плоскости
, то возникает предельный случай: обе ветви смыкаются в одну линию и образуют правую полуось. Действительная ось отображается на правую полуось в плоскости 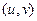 .
.
Аналогично, для какой-либо вертикальной прямой:
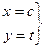
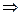
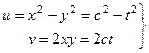 . Тогда, исключая параметр
. Тогда, исключая параметр 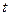 , получим
, получим 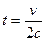
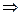
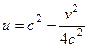 . Это параболы, направленные ветвями влево, симметричные тем, что были рассмотрены чуть выше.
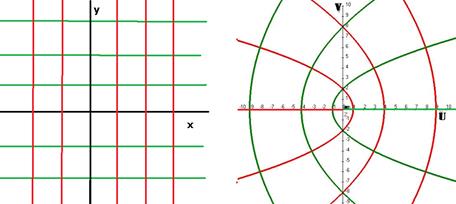
. Это параболы, направленные ветвями влево, симметричные тем, что были рассмотрены чуть выше.
На чертеже зелёным цветом показаны горизонтальные прямые и их образы при отображении  , а красным - вертикальные прямые и их образы:
, а красным - вертикальные прямые и их образы:
Пример. Разложить  на действительную и мнимую часть.
на действительную и мнимую часть.
Используем то, что нашли ранее: 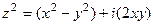 , тогда
, тогда
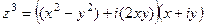 =
=  =
= 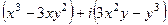 .
.
Здесь 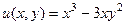
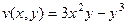
Пример. Разложить 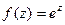 на действительную и мнимую часть.
на действительную и мнимую часть.
По формуле Эйлера:  =
= 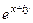 =
= 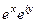 =
= 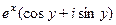 =
= 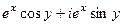 , тогда
, тогда 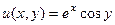 ,
, 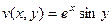 .
.
Изучим деформации плоскости при действии линейной функции вида  , где коэффициенты
, где коэффициенты  ,
, 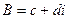 это тоже некоторые комплексные числа. При этом очевидно, что
это тоже некоторые комплексные числа. При этом очевидно, что 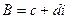 приводит к сдвигу плоскости на вектор
приводит к сдвигу плоскости на вектор 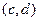 , поэтому сначала более подробно изучим именно
, поэтому сначала более подробно изучим именно 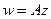 без сдвига.
без сдвига.
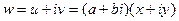 =
= 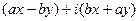 . Но такое отображение можно представить с помощью линейного оператора:
. Но такое отображение можно представить с помощью линейного оператора:
 =
= 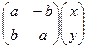 .
.
Введём величину 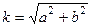 , тогда существует какой-то угол
, тогда существует какой-то угол 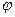 , для которого
, для которого 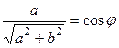 ,
, 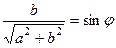 . Причём заметим, что это именно
. Причём заметим, что это именно 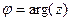 ,
, 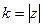 для исходного комплексного числа.
для исходного комплексного числа.
Тогда матрица линейного оператора имеет вид: 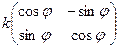 то есть это композиция растяжения и поворота плоскости, причём поворот на угол
то есть это композиция растяжения и поворота плоскости, причём поворот на угол  , а растяжение или сжатие на
, а растяжение или сжатие на  .
.
(ДОК 12). Доказать что линейное отображение  в комплексной плоскости есть композиция растяжения, поворота и сдвига.
в комплексной плоскости есть композиция растяжения, поворота и сдвига.
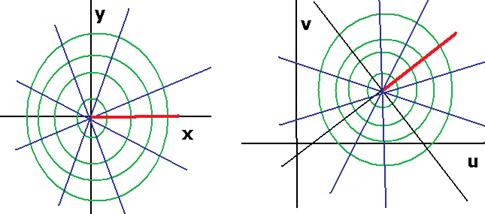
На этом чертеже показано, как изменяется плоскость при линейном отображении. Красным веделено горизонтальное направление, после отображения оно повёрнуто.
Замечание. Отображение 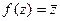 соответствует зеркальному отражению плоскости, т.е. оно не сводится к композиции поворота и растяжения.
соответствует зеркальному отражению плоскости, т.е. оно не сводится к композиции поворота и растяжения.
ЛЕКЦИЯ 5. 03.10.2018
Доказательство. (ДОК 15).
Запишем 2 условия Коши-Римана. Одно продифференцируем по переменной  , а второе по
, а второе по 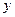 :
:


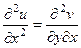
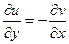
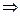
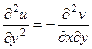 .
.
Сложим теперь эти 2 равенства, но при этом смешанные производные 2 порядка от 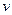 при этом совпадают, они вычитаются и дают 0.
при этом совпадают, они вычитаются и дают 0.
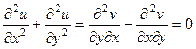 . Итак,
. Итак, 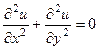 .
.
Теперь снова запишем условия Коши-Римана, 1-е дифференцирует по  , а второе по
, а второе по  .
.

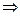
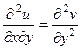
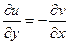
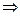
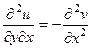 .
.
Теперь вычтем из 1-го равенства 2-е.
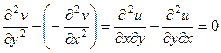 , тогда
, тогда 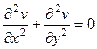 .
.
□
Пример. 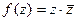 =
=  . Здесь для
. Здесь для 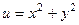 не верно уравнение Лапласа:
не верно уравнение Лапласа:  .
.
Теорема 4. Условия Коши-Римана эквивалентны условию 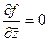 .
.
Доказательство (ДОК 16). Вспомним, что  можно выразить через
можно выразить через 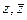 таким образом:
таким образом: 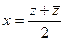 ,
, 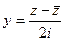 . Сделаем это в функциях
. Сделаем это в функциях  .
.
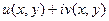 =
= 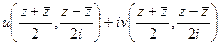 .
.
Таким образом, функция стала выражена через два аргумента 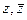 , а значит, можно искать частную производную по
, а значит, можно искать частную производную по  .
.
Вспомним формулу полной производной (из 1 семестра) для случая композиции типа  :
:  . Найдём производные от
. Найдём производные от 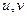 по
по  этим методом, причём здесь тоже промежуточные переменные
этим методом, причём здесь тоже промежуточные переменные  .
.
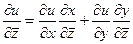 ,
, 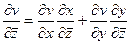 .
.
При этом такие компоненты как 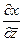 и
и 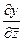 можно найти
можно найти
из формул 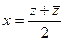 ,
, 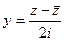 , а именно :
, а именно :
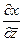 =
= 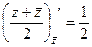 ,
,  =
= 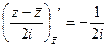 . Таким образом,
. Таким образом,
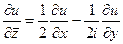 ,
, 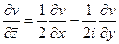 .
.
Тогда 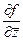 =
= 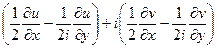 =
=
 =
=  =
=
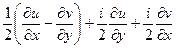 =
= 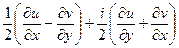 .
.
Выполнение условий Коши-Римана 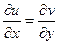

в данном случае как раз и эквивалентно тому, что в обеих скобках нули, то есть 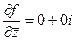 .
.
□
Итак, как видим, наличие 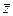 в составе функции приводит к недифференцируемости. Впрочем, то же верно и при наличии
в составе функции приводит к недифференцируемости. Впрочем, то же верно и при наличии 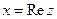 или
или 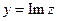 , в составе которых есть элемент
, в составе которых есть элемент  .
.
ЛЕКЦИЯ 6. 10.10.2018
Решение.
А) 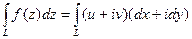 =
= 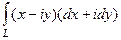 =
=
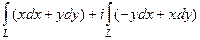 , далее вычисляем 2 криволинейных интеграла по отрезку, на котором
, далее вычисляем 2 криволинейных интеграла по отрезку, на котором 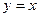 , заменяем
, заменяем 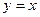 ,
, 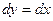 .
.
При этом 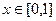 .
. 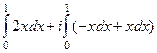 =
= 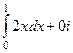 =
=  .
.
Б) Исходное раскрытие скобок происходит так же, как и в прошлом случае:  но теперь линия
но теперь линия  это не отрезок, заданный явным уравнением
это не отрезок, заданный явным уравнением 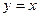 , а парабола, заданная явным уравнением
, а парабола, заданная явным уравнением 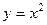 . Поэтому заменяем
. Поэтому заменяем 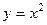 ,
, 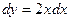 .
.
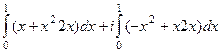 =
= 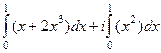 =
=
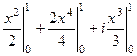 =
= 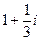 .
.
Ответ. по отрезку: 1, по параболе: 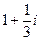 .
.
Как видим, в зависимости от формы кривой могут получиться разные ответы, но это здесь потому, что функция не аналитическая, она содержит 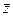 , а мы доказывали теорему 4 в конце прошлого § о том, что аналитичность равносильна отсутствию
, а мы доказывали теорему 4 в конце прошлого § о том, что аналитичность равносильна отсутствию  в составе функции, то есть тому, что
в составе функции, то есть тому, что 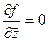 .
.
Теорема 1. Если 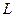 замкнутый контур, внутри которого во всех точках
замкнутый контур, внутри которого во всех точках 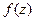 является аналитической, то
является аналитической, то 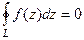 .
.
(ДОК 17). Доказательство. 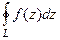 =
=  =
=
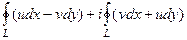 в двух этих интегралах - циркуляция двух векторных полей
в двух этих интегралах - циркуляция двух векторных полей 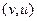 и
и 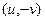 , они потенциальны по теореме 2 прошлого §, а тогда циркуляция равна 0, то есть получаем
, они потенциальны по теореме 2 прошлого §, а тогда циркуляция равна 0, то есть получаем 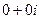 .
.
Теорема 2. Если 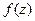 является аналитической во всех точках некоторой области
является аналитической во всех точках некоторой области 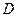 , граница которой односвязна, то интеграл от функции
, граница которой односвязна, то интеграл от функции 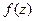 не зависит от пути, то есть имеет одно и то же значение для любой кривой
не зависит от пути, то есть имеет одно и то же значение для любой кривой 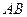 , соединяющей пару точек
, соединяющей пару точек 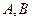 .
.
(ДОК 18). Доказательство. Аналогично прошлой теореме,
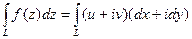 =
= 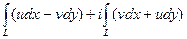 .
.
Криволинейные интегралы 2 рода от векторных полей 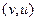 и
и  не зависят от пути, что доказано ранее в главе «теория поля».
не зависят от пути, что доказано ранее в главе «теория поля».
Так как для аналитической функции интеграл не зависит от пути, то для аналитической функции оказывается возможным ввести понятие первообразной. Введём в рассмотрение такую функцию: 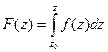 которая каждой точке ставит в соответствие интеграл до неё от некоторой фиксированной точки
которая каждой точке ставит в соответствие интеграл до неё от некоторой фиксированной точки  . Вводится по аналогии с вычислением потенциала поля, только в данном случае, вычисляются потенциалы двух полей
. Вводится по аналогии с вычислением потенциала поля, только в данном случае, вычисляются потенциалы двух полей 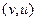 и
и  . Докажем, что построенная таким образом функция является первообразной.
. Докажем, что построенная таким образом функция является первообразной.
Теорема 3. Функция 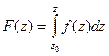 является первообразной от функции
является первообразной от функции 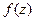 .
.
(ДОК 19). Доказательство.
Докажем, что производная от  равна
равна 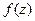 .
.
По определению производной, 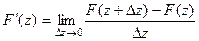 .
.
Распишем разность в числителе более подробно.
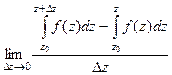 =
= 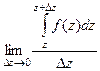 .
.
потому что по свойству 2, в числителе сокращается интеграл по той части, которая от 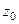 до
до  , и остаётся только от
, и остаётся только от  до
до 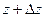 .
.
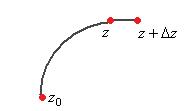
Итак, остаётся доказать равенство: 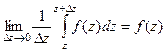 , которое можно переписать в виде
, которое можно переписать в виде  .
.
Распишем более подробно действительную и мнимую часть как в интеграле, так и в правом пределе.
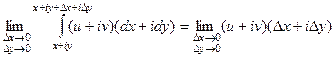
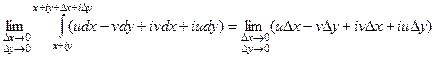
Проведём исследование 1 из 4 слагаемых, остальные по аналогии.
Если рассматривать в проекции на горизонтальную ось, допустим, что  фиксировано, то:
фиксировано, то:
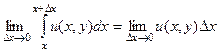 что эквивалентно
что эквивалентно
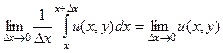 .
.
Но так как для непрерывной функции действительного переменного верна теорема о среднем, т.е. такое свойство: 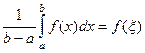 , то в данном случае можно утверждать, что существует такая точка
, то в данном случае можно утверждать, что существует такая точка 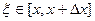 , что выполняется
, что выполняется 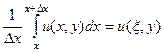 , причём при
, причём при 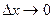 точка
точка 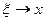 , ведь она находится на отрезке, который стягивается в одну точку, в свою левую границу.
, ведь она находится на отрезке, который стягивается в одну точку, в свою левую границу.
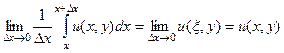 . Итак, мы исследовали 1-е слагаемое из 4-х, остальные аналогично, причём везде используются только функции действительного переменного, просто одни из них умножаются на
. Итак, мы исследовали 1-е слагаемое из 4-х, остальные аналогично, причём везде используются только функции действительного переменного, просто одни из них умножаются на 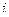 в итоговой записи, а другие нет. Но для каждого элемента при этом можно использовать теорему о среднем как для действительной функции.
в итоговой записи, а другие нет. Но для каждого элемента при этом можно использовать теорему о среднем как для действительной функции.
Теорема 4. Для аналитической на кривой 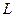 функции верна формула Ньютона-Лейбница:
функции верна формула Ньютона-Лейбница: 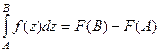 .
.
(ДОК 20). Доказательство. По построению первообразной,
 и
и  .
.
Но тогда 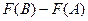 =
= 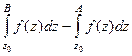 а тогда по 3-му свойству
а тогда по 3-му свойству
это 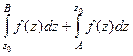 , что равно интегралу по кривой, проходящей от
, что равно интегралу по кривой, проходящей от 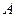 до
до  (через точку
(через точку  ).
).
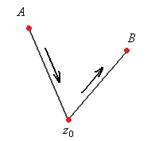
Тогда 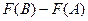 =
= 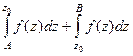 =
= 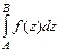 т.к. по свойству 2, их можно объединить. Итак,
т.к. по свойству 2, их можно объединить. Итак, 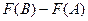 =
= 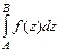 .
.
Пример. Вычислить  от 0 до
от 0 до 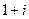 двумя способами:
двумя способами:
А) без формулы Б) по формуле Ньютона-Лейбница.
Решение.
А)  =
= 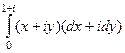 =
= 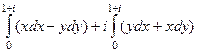
Пусть точки 0 и 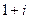 соединены по прямой
соединены по прямой 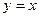 (вспомним, что интеграл не зависит от пути, поэтому можем соединить их как удобнее для вычислений). Тогда
(вспомним, что интеграл не зависит от пути, поэтому можем соединить их как удобнее для вычислений). Тогда 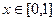 ,
, 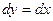 , и
, и
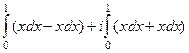 =
= 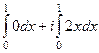 =
= 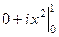 =
= 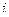 .
.
Б) По формуле: 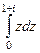 =
= 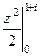 =
= 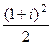 =
=  =
= 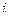 .
.
Пример. Вычислить 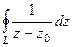 , где
, где  - окружность радиуса
- окружность радиуса 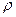 вокруг точки
вокруг точки 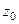
Решение.
Способ 1. Представим функцию в виде  . Движение по окружности можно задать формулами:
. Движение по окружности можно задать формулами:
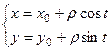
В этом случае 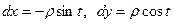 . Тогда
. Тогда
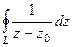 =
= 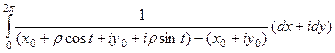 =
=
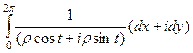 , домножим на сопряжённое,
, домножим на сопряжённое, 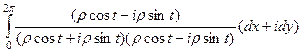 =
=
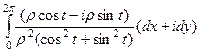 =
= 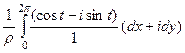 =
=
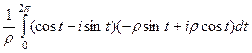 =
= 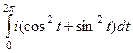 =
=
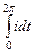 =
= 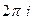 .
.
Способ 2. Представим 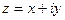 =
= 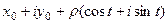 =
=
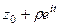 . Тогда
. Тогда 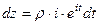 .
.
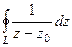 =
=  =
= 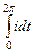 =
= 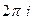 .
.
ЛЕКЦИЯ 7. 17.10.2018
Интегральная формула Коши
Заметим, что в последнем примере в конце прошлой лекции 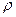 сократилось и ответ вообще не зависел от
сократилось и ответ вообще не зависел от 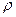 - радиуса окружности. То есть получается, при уменьшении или увеличении окружности ничего не изменится, если та же самая точка разрыва остаётся внутри, а замкнутый контур стягивается к ней, оставляя снаружи область аналитичности. Этот факт докажем в общем случае.
- радиуса окружности. То есть получается, при уменьшении или увеличении окружности ничего не изменится, если та же самая точка разрыва остаётся внутри, а замкнутый контур стягивается к ней, оставляя снаружи область аналитичности. Этот факт докажем в общем случае.
Теорема 1. (Интегральная теорема Коши).
Пусть  некоторый замкнутый контур,
некоторый замкнутый контур, 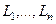 - n замкнутых непересекающихся контуров, лежащих внутри
- n замкнутых непересекающихся контуров, лежащих внутри  . Функция
. Функция 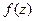 является аналитической на всех этих контурах, а также внутри
является аналитической на всех этих контурах, а также внутри 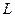 , но вне
, но вне  . Тогда
. Тогда  .
.
Доказательство (ДОК 21).
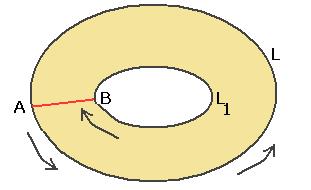
Для того, чтобы лучше понять идею доказательства, рассмотрим сначала ситуацию, когда внутри  расположен один контур
расположен один контур 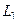 , то есть оласть аналитичности - кольцо. Можно взять какую-либо пару точек
, то есть оласть аналитичности - кольцо. Можно взять какую-либо пару точек 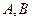 на
на 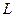 и
и  соответственно (чтобы точкибыли максимально близко напротив друг друга) и соединить их отрезком. Тогда для комбинированого контура, состоящего из 4 частей:
соответственно (чтобы точкибыли максимально близко напротив друг друга) и соединить их отрезком. Тогда для комбинированого контура, состоящего из 4 частей:  ,
, 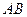 ,
, 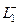 ,
, 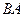 внутренняя область, похожая на кольцо с разрезом, это область аналитичности. Мы один раз обходим этот контур, двигаясь по внешнему против часовой стрелки, поэтому и обозначено
внутренняя область, похожая на кольцо с разрезом, это область аналитичности. Мы один раз обходим этот контур, двигаясь по внешнему против часовой стрелки, поэтому и обозначено 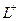 , затем переходя на внутренний контур по
, затем переходя на внутренний контур по 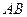 , затем двигаясь по внутреннему в противоположном направлении (
, затем двигаясь по внутреннему в противоположном направлении (  ), и возвращаясь по
), и возвращаясь по 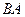 снова на внешний контур. Чертёж:
снова на внешний контур. Чертёж:
Но если комбинированный контур окружает область аналитичности, то интеграл по нему равен 0.
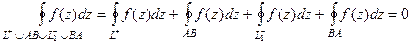 .
.
При этом интегралы по  и
и  и так взаимно уничтожаются, поэтому
и так взаимно уничтожаются, поэтому  . Но если сменить направление движение по внутреннему контуру
. Но если сменить направление движение по внутреннему контуру  , то интеграл по нему сменил бы знак, тогда:
, то интеграл по нему сменил бы знак, тогда: 
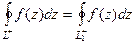 .
.
Таким образом, интегралы по  и
и  одинаковы, то есть можно без изменения результата уменьшить область, стянув её к точке разрыва, оставив снаружи какую-то часть области аналитичности.
одинаковы, то есть можно без изменения результата уменьшить область, стянув её к точке разрыва, оставив снаружи какую-то часть области аналитичности.

Если внутри  несколько контуров, внутри которых нарушена аналитичности или даже существование функции, то применяется похожая схема рассуждений, только надо поочерёдно соединить отрезком
несколько контуров, внутри которых нарушена аналитичности или даже существование функции, то применяется похожая схема рассуждений, только надо поочерёдно соединить отрезком 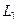 с
с 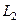 , затем
, затем 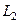 с
с  и так далее, до номера n.
и так далее, до номера n.
Теорема 2. (Интегральная формула Коши).
Пусть 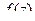 является аналитической на контуре
является аналитической на контуре 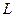 и внутри него, точка
и внутри него, точка 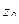 лежит внутри
лежит внутри 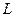 . Тогда
. Тогда 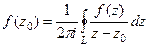 .
.
Доказательство (ДОК 22).
В рассмотренном примере в конце прошлой лекции мы вычислили  , то есть верно
, то есть верно 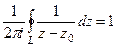 . Но мы можем домножить это равенство на любую комплексную константу, и тогда:
. Но мы можем домножить это равенство на любую комплексную константу, и тогда: 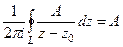 . Впрочем, тогда это же верно и для константы
. Впрочем, тогда это же верно и для константы 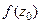 : получаем
: получаем  . Мы получили выражение, очень похожее на то, которое надо доказать, но ещё не то: ведь здесь в числителе константа, а не функция. Вот если мы теперь ещё и докажем, что
. Мы получили выражение, очень похожее на то, которое надо доказать, но ещё не то: ведь здесь в числителе константа, а не функция. Вот если мы теперь ещё и докажем, что 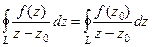 , или то же самое, что
, или то же самое, что 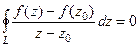 , то требуемое утверждение будет верно.
, то требуемое утверждение будет верно.
Рассмотрим функцию  . Это функция, которая участвует в определении предела, ведь
. Это функция, которая участвует в определении предела, ведь 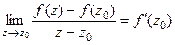 .
.
Таким образом, 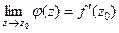 , то есть
, то есть 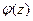 имеет конечный предел в точке
имеет конечный предел в точке 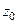 , а это значит, что она ограничена в окрестности этой точки,
, а это значит, что она ограничена в окрестности этой точки, 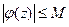 . По теореме 1 (интегральная теорема Коши), интеграл по
. По теореме 1 (интегральная теорема Коши), интеграл по 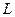 можно заменить на интеграл по любой малой окружности
можно заменить на интеграл по любой малой окружности 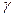 радиуса
радиуса  , лежащей внутри
, лежащей внутри 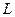 , результат при этом не изменится. Тогда
, результат при этом не изменится. Тогда 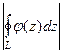 =
= 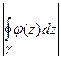
 , где
, где 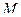 - максимальное значение модуля функции,
- максимальное значение модуля функции, 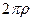 - длина кривой, по которой происходит интегрирование. Но ведь по теореме 1 это должно быть верно для какого угодно малого
- длина кривой, по которой происходит интегрирование. Но ведь по теореме 1 это должно быть верно для какого угодно малого  . То есть
. То есть  меньше или равен любой бесконечно-малой величины. Тогда этот интеграл равен 0. То есть
меньше или равен любой бесконечно-малой величины. Тогда этот интеграл равен 0. То есть 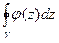 =
= 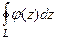 =
= 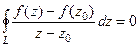 . Значит,
. Значит, 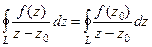 , а тогда:
, а тогда:
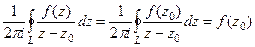 , т.е.
, т.е. 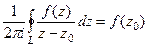 доказано в итоге.
доказано в итоге.
Интегральная формула Коши позволяет быстро вычислять интегралы по контуру вокруг точки разрыва, фактически не проводя подробное интегрирование. Достаточно убрать из знаменателя ту скобку  , которая соответствует этой точке разрыва, подставить в остальную функцию
, которая соответствует этой точке разрыва, подставить в остальную функцию  и домножить на
и домножить на 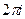 .
.
Пример. Вычислить 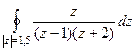 .
.
Решение. Внутри окружности радиуса 1,5 всего одна из двух точек разрыва функции, вторая снаружи. Обозначим в качестве 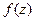 функцию без
функцию без 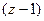 , как будто на
, как будто на 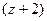 делим чуть раньше, а на
делим чуть раньше, а на 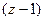 позже.
позже.
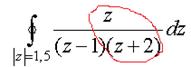
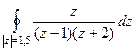 =
= 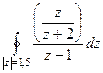 , где
, где 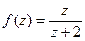 это то, что именно обозначается
это то, что именно обозначается 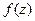 в интегральной формуле Коши.
в интегральной формуле Коши.
Тогда 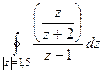 =
=  =
=  =
= 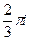 . \
. \
Ответ. 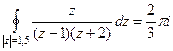 .
.
Теорема 3. (Обобщённая интегральная формула Коши).
Пусть 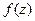 является аналитической на контуре
является аналитической на контуре 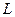 и внутри него, точка
и внутри него, точка 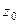 лежит внутри
лежит внутри 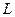 . Тогда
. Тогда 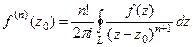 .
.
Доказательство (ДОК 23).
Продифференцируем по параметру 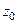 правую и левую часть равенства в исходной интегральной формуле Коши.
правую и левую часть равенства в исходной интегральной формуле Коши.
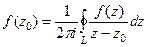 .
.
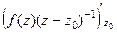 =
=  =
= 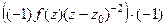 =
= 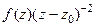 =
= 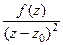 .
.
Таким образом, 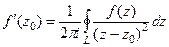 .
.
Следующая производная от  равна
равна
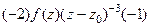 =
= 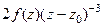 . Аналогично следующая (тертья от исходной функции) равна
. Аналогично следующая (тертья от исходной функции) равна 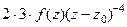 , далее по индукции для n-й производной получим
, далее по индукции для n-й производной получим  =
=  . Тогда
. Тогда 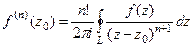 .
.
Рассмотрим примеры, похожие на предыдущий, но в которых будет 2 или 3 степень скобки 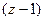 . По обобщённой интегральной формуле Коши, если скобка во 2 степени, надо не просто убрать её из знаменателя, а после этого ещё и один раз продифференцировать оставшуюся функцию, и лишь затем подставлять
. По обобщённой интегральной формуле Коши, если скобка во 2 степени, надо не просто убрать её из знаменателя, а после этого ещё и один раз продифференцировать оставшуюся функцию, и лишь затем подставлять  . А если 3 степень, то 2 раза продифференцировать, но с 3-й степени начинает ещё и изменяться коэффициент из-за того, что он уже не равен 1, а будет
. А если 3 степень, то 2 раза продифференцировать, но с 3-й степени начинает ещё и изменяться коэффициент из-за того, что он уже не равен 1, а будет  .
.
Пример. Вычислить 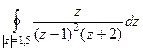 .
.
Решение. 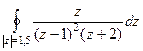 =
=  =
= 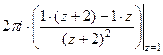 =
=  =
=  =
=  .
.
Ответ. 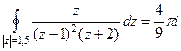 .
.
Пример. Вычислить  .
.
Решение. 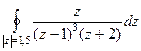 =
= 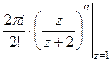 =
= 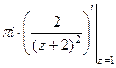 =
=
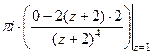 =
= 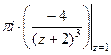 =
=  =
= 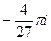 .
.
Ответ. 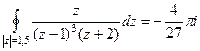 .
.
Далее докажем с помощью интегральной формулы Коши, что верно разложение в ряд Тейлора не только для функций действительного переменного (1 семестр), но и для комплексных функций.
Теорема 4. (Теорема о разложении в ряд Тейлора).
Пусть 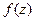 является аналитической в окрестности точки
является аналитической в окрестности точки 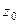 .
.
Тогда она представима в виде степенного ряда:
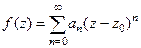 , где
, где  .
.
Доказательство (ДОК 24).
Рассмотрим окрестность точки 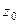 и какую-нибудь точку
и какую-нибудь точку 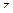 , лежащую внутри неё. Пусть граница окрестности - кривая
, лежащую внутри неё. Пусть граница окрестности - кривая  , а точку на ней обозначим
, а точку на ней обозначим 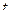 .
.

Можно записать интегральную формулу Коши для точки 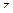 в таком виде:
в таком виде: 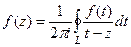 (здесь
(здесь 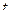 и
и  имеют такой же смысл, как ранее было
имеют такой же смысл, как ранее было 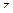 и
и 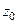 ).
).
Изучим дробь 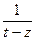 подробнее. Можно прибавить и отнять
подробнее. Можно прибавить и отнять 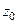 :
:
 =
= 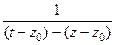 а дальше преобразовать к виду суммы геометрической прогрессии, чтоб воспользоваться тем фактом, что
а дальше преобразовать к виду суммы геометрической прогрессии, чтоб воспользоваться тем фактом, что 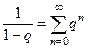 . Причём выносить за скобку в знаменателе надо именно такой из двух блоков, чтобы получилось 1 и нечто меньшее по модулю, чем 1. Учитывая, что
. Причём выносить за скобку в знаменателе надо именно такой из двух блоков, чтобы получилось 1 и нечто меньшее по модулю, чем 1. Учитывая, что 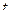 на границе, а
на границе, а 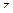 внутри контура, то
внутри контура, то 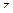 ближе к
ближе к 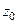 , чем
, чем 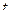 . Поэтому
. Поэтому 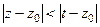 , т.е.
, т.е. 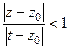
Тогда 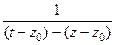 =
=  =
= 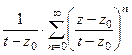 =
=
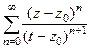 . Подставим это выражение в интегральную формулу Коши вместо
. Подставим это выражение в интегральную формулу Коши вместо 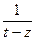 . Тогда
. Тогда 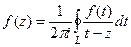 =
= 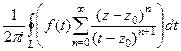 =
= 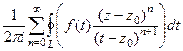 .
.
Оставим внутри знака интеграла только те множители, которые зависят от 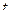 . Получим
. Получим 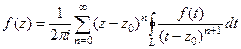 но оставшийся внутри суммы интеграл можно преобразовать по обобщённой интегральной формуле Коши из теоремы 3, ведь если
но оставшийся внутри суммы интеграл можно преобразовать по обобщённой интегральной формуле Коши из теоремы 3, ведь если 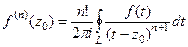 то
то 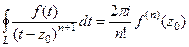 .
.
Тогда 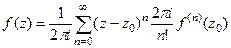 =
= 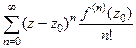 .
.
Получилось разложение в ряд Тейлора с коэффициентами 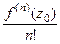 .
.
Теорема 5. (Теорема о разложении в ряд Лорана).
Пусть 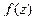 является аналитической в некотором кольце с центром
является аналитической в некотором кольце с центром 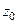 , тогда она представима в виде ряда
, тогда она представима в виде ряда 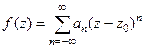 .
.
Доказательство (ДОК 25).
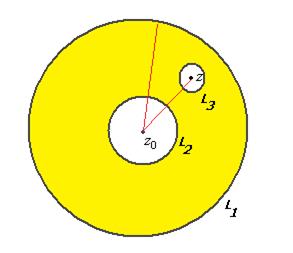
Обозначим внутреннюю и внешнюю границы кольца через  и
и 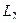 . Возьмём произвольную точку
. Возьмём произвольную точку 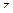 в кольце. Окружим её контуром
в кольце. Окружим её контуром  малого радиуса, так, чтобы он не пересекался с
малого радиуса, так, чтобы он не пересекался с 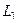 и
и 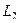 .
.
По теореме 1, 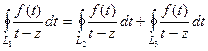 , впрочем, тогда
, впрочем, тогда
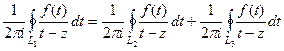 . Но третий интеграл по контуру
. Но третий интеграл по контуру  , внутри которого только одна точка нарушения аналитичности функции
, внутри которого только одна точка нарушения аналитичности функции 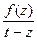 , а именно точка
, а именно точка  . Тогда третий интеграл сразу можно по интегральной формуле Коши представить в виде значения функции:
. Тогда третий интеграл сразу можно по интегральной формуле Коши представить в виде значения функции:
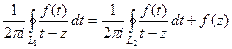 .
.
Тогда 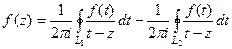 .
.
В каждом из интегралов преобразуем выражение 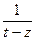 с помощью геометрической прогрессии. В первом из них почти как в предыдущей теореме, потому что
с помощью геометрической прогрессии. В первом из них почти как в предыдущей теореме, потому что 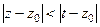 , т.е.
, т.е. 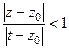 . А вот во втором, преобразование будет чуть иначе, потому что для точки
. А вот во втором, преобразование будет чуть иначе, потому что для точки 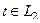 , наоборот,
, наоборот, 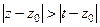 и соответственно,
и соответственно,  .
.
Если 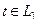 :
:  =
= 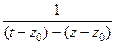 =
= 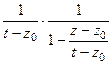 =
= 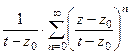 =
= 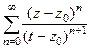 .
.
Если 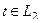 :
: 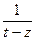 =
= 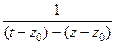 =
=  =
=
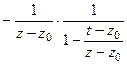 =
= 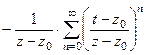 =
= 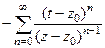 .
.
Тогда 
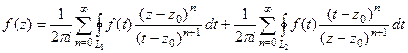 =
=
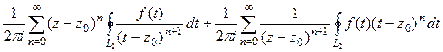
В первой части снова по обобщённой интегральной формуле Коши,
а во 2 части сделаем сдвиг индексов на 1 пункт.
 =
=
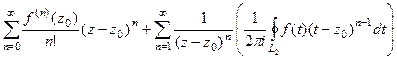 .
.
Мы получили такую структуру ряда, где представлены все целые степени, и положительные, и отрицательные:
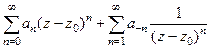 ,
,
а если бы мы ещё сделали замену индекса 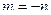 для 2 части, чтобы подчеркнуть, что там именно отрицательные степени, то получили бы
для 2 части, чтобы подчеркнуть, что там именно отрицательные степени, то получили бы
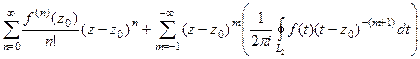
где 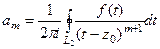 т.е. коэффициенты при отрицательных степенях во 2 части приобрели бы точно такой же вид, как и в 1 части, с той разницей лишь, что
т.е. коэффициенты при отрицательных степенях во 2 части приобрели бы точно такой же вид, как и в 1 части, с той разницей лишь, что 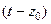 с отрицательной степенью в знаменателе, хоть и формально написан в знаменателе, но реально располагается в числителе. Так, например,
с отрицательной степенью в знаменателе, хоть и формально написан в знаменателе, но реально располагается в числителе. Так, например,
 ,
, 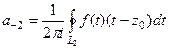 .
.
ЛЕКЦИЯ 8. 24.10.2018
Сначала рассмотрим ещё некоторые примеры на интегральную формулу Коши, которую мы доказали на прошлой лекции.
Пример. Вычислить  .
.
Решение. Здесь степень множителя в знаменателе равна 2. Есть всего одна точка разрыва, а именно 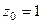 . Конкретизируем обобщённую интегральную формулу Коши для этого случая.
. Конкретизируем обобщённую интегральную формулу Коши для этого случая.
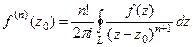 , при n = 1 получается
, при n = 1 получается
 =
= 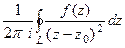 .
.
Отсюда следует, что 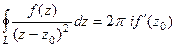
Тогда 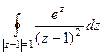 =
= 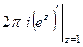 =
= 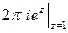 =
= 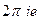 .
.
Ответ. 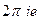 .
.
Пример. Доказать, что 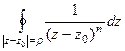 = 0 для любого целого числа
= 0 для любого целого числа 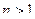 .
.
Решение. Здесь по обобщённой интегральной формуле Коши при любом n получается, что 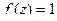 . Затем любая производная от константы есть 0. Поэтому результат всегда 0.
. Затем любая производная от константы есть 0. Поэтому результат всегда 0.
Впрочем, если бы мы вычисляли даже старым способом без интегральной формулы Коши (как в конце лекции 6 на странице 56), то получалось бы 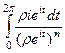 =
= 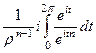 =
= 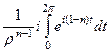 =
=
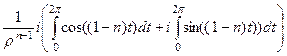 но оба интеграла здесь равны 0, потому что
но оба интеграла здесь равны 0, потому что  целое число, а значит, на отрезке
целое число, а значит, на отрезке 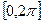 один или больше полных периодов, что приводит к нулевому интегралу. И лишь при
один или больше полных периодов, что приводит к нулевому интегралу. И лишь при 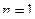 результат получается
результат получается 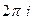 (а это было в примере на стр. 56 в конце лекции 6).
(а это было в примере на стр. 56 в конце лекции 6).
Кватернионы.
Указанные выше причины не препятствуют построению числовых систем в случае чётной размерности. Так, если сделать по аналогии перехода от действительных чисел к комплексным, удвоить размерность и образовать числа вида 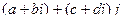 из пары комплексных чисел, где второе умножено ещё на какой-то объект
из пары комплексных чисел, где второе умножено ещё на какой-то объект 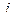 , то получается 4-мерная система с тремя мнимыми единицами и числами вида
, то получается 4-мерная система с тремя мнимыми единицами и числами вида 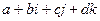 , которые называются кватернионами.
, которые называются кватернионами.
При этом  это мы изначально называем произведение 1-й и 2-й мнимых единиц некоторой третьей мнимой единицей.
это мы изначально называем произведение 1-й и 2-й мнимых единиц некоторой третьей мнимой единицей.
Получается антикоммутативная система с умножением:
 ,
, 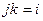 ,
, 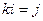 ,
, 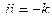 ,
,  ,
, 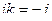 .
.
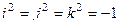 . Умножение на 1 сохраняет любой объект неизменным. Получается таблица:
. Умножение на 1 сохраняет любой объект неизменным. Получается таблица:
Таблица умножения базисных элементов системы кватернионов.
| 1 | 
| 
| 
| |
| 1 | 1 | 
| 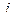
| 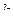
|
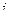
| 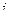
| 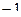
| 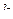
| 
|
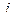
| 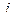
| 
| 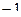
| 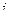
|
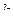
| 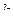
| 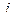
| 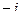
| 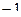
|
Обратите вниание, что законы умножения в системе кватернионов 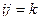 ,
, 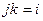 ,
, 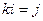 легко запомнить, если представить с помощью цикла:
легко запомнить, если представить с помощью цикла:
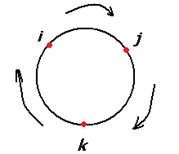
При умножении каждой пары получается следующий, если двигаться строго по часовой стрелке. Ещё обратите внимание, что мнимые единицы системы кватернионов подчиняются таким же законам, как векторное умножение в 3-мерном пространстве. Там тоже 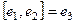 ,
, 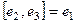 ,
,  . Векторное произведение пары векторов есть общий перпендикулярк ним, причём так чтобы получалась правоориентированная тройка. Векторное умножение было придумано Гамильтоном в 1843 году как раз одновременно с системой кватернионов.
. Векторное произведение пары векторов есть общий перпендикулярк ним, причём так чтобы получалась правоориентированная тройка. Векторное умножение было придумано Гамильтоном в 1843 году как раз одновременно с системой кватернионов.
Как и для комплексных чисел, здесь есть понятие «сопряжённый кватернион». Если 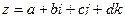 то
то 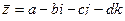 . При этом
. При этом 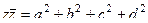 , то есть можно также ввести понятие модуля кватерниона:
, то есть можно также ввести понятие модуля кватерниона: 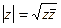 =
= 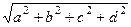 .
.
Подробнее о том, почему получается 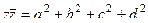 .
.
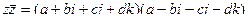 =
=
 =
=
 но система антикоммутативна, т.е.
но система антикоммутативна, т.е.  , поэтому все эти суммы в скобках равны 0, вот и остаётся
, поэтому все эти суммы в скобках равны 0, вот и остаётся 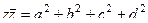 .
.
Нули аналитической функции.
Определение. Точка  называется нулём функции
называется нулём функции 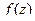 , если
, если 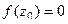 .
.
Мы сначала изучим нули функции, для того, чтобы затем изучить более подробно типы точек разрыва. Если  является нулём для
является нулём для 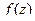 то в этой же точке предел
то в этой же точке предел 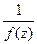 равен
равен 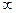 .
.
Вспомним, что в 1 семестре было ещё название «бесконечно-малая» и «бесконечно-большая» функция в точке. Бесконечно-малые могли быть разных порядков. Есть и здесь аналогичное более подробное определение, различающее порядки бесконечно малых:
Определение. Точка  называется нулём порядка m функции
называется нулём порядка m функции 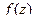 , если
, если 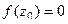 и функция представима в виде
и функция представима в виде 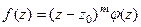 , где
, где 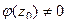 .
.
Кстати, здесь ещё можно напомнить, что для многочленов тоже было известно понятие корня кратности m, и аналогия тут прямая.
Теорема 1. (О виде ряда Тейлора в окрестности нуля порядка m).
Если  нуль порядка m функции
нуль порядка m функции 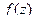 , то ряд Тейлора имеет вид
, то ряд Тейлора имеет вид
 т.е. начинается именно со степени m.
т.е. начинается именно со степени m.
Доказательство (ДОК 27). Если 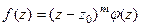 , где
, где 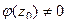 , то ряд Тейлора функции
, то ряд Тейлора функции 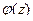 обязательно начинается с константы, а иначе не было бы
обязательно начинается с константы, а иначе не было бы 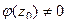 . Тогда:
. Тогда:
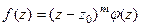 =
= 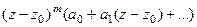
что и приводит к виду 
Теорема 2. (Об изолированности нулей).
Если  является нулём порядка m функции
является нулём порядка m функции 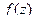 , то существует окрестность
, то существует окрестность 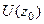 , не содержащая других нулей этой функции.
, не содержащая других нулей этой функции.
Доказательство (ДОК 28). Если  является нулём порядка m функции
является нулём порядка m функции 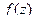 , то
, то 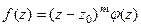 . Первый множитель обращается в 0 только в самой точке
. Первый множитель обращается в 0 только в самой точке  и нигде больше. Второй в точке
и нигде больше. Второй в точке  отличен от 0. Но
отличен от 0. Но 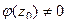 , а так как эта функция аналитическая и значит, непрерывная, то существует окрестность
, а так как эта функция аналитическая и значит, непрерывная, то существует окрестность 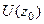 , в которой
, в которой 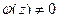 т.е. не обращается в 0 ни в одной её точке. Итак, есть произведение двух множителей, где первый равен 0 только в
т.е. не обращается в 0 ни в одной её точке. Итак, есть произведение двух множителей, где первый равен 0 только в  , а второй нигде в окрестности
, а второй нигде в окрестности 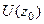 . Таким образом, в
. Таким образом, в 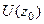 произведение обращается в 0 только в
произведение обращается в 0 только в  .
.
Следствие 1. Если существует последовательность нулей функции, сходящаяся к  , то в некоторой окрестности
, то в некоторой окрестности 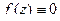 .
.
ЛЕКЦИЯ 9. 31.10.2018
Особые точки
Определение. Точка  называется правильной точкой функции
называется правильной точкой функции 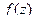 , если
, если 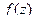 является аналитической в
является аналитической в  , и особой точкой, если она не является аналитической в
, и особой точкой, если она не является аналитической в  .
.
Определение. Точка  называется изолированной особой точкой, если в некоторой её окрестности
называется изолированной особой точкой, если в некоторой её окрестности 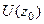 нет других особых точек.
нет других особых точек.
Существует такая классификация особых точек в зависимости от предела 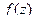 .
.
| Название | Устранимая особая точка | Полюс | Существенно-особая точка |
| При каком условии | 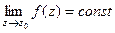
| 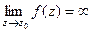
| 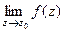 не существует
не существует
|
Пример
(  ) )
| 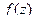 = = 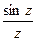
| 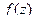 = = 
| 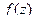 = = 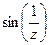
|
Теорема 1. Точка  является нулём функции
является нулём функции 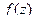
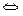 она является полюсом функции
она является полюсом функции 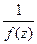 .
.
Доказательство. Точка  является нулём функции
является нулём функции 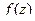
 функция
функция 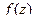 представима в виде
представима в виде 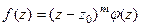 , причём
, причём
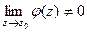 . Это эквивалентно тому, что
. Это эквивалентно тому, что 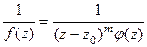 =
=
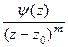 , где
, где 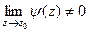 , а предел знаменателя равен 0. Это означает, что
, а предел знаменателя равен 0. Это означает, что 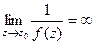 .
.
В связи с этим, естественным образом возникает определение полюса порядка 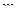 : точка
: точка  называется полюсом порядка m для функции
называется полюсом порядка m для функции 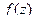 , если для функции
, если для функции 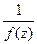 она является нулём порядка m.
она является нулём порядка m.
Теорема 2.
(О взаимосвязи типа особой точки и строения ряда Лорана).
1).  устранимая особая точка
устранимая особая точка 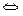 остутствует главная часть ряда Лорана.
остутствует главная часть ряда Лорана.
2)  полюс
полюс 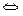 главная часть ряда Лорана содержит конечное количество слагаемых.
главная часть ряда Лорана содержит конечное количество слагаемых.
3)  существенно-особая точка
существенно-особая точка 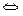 главная часть ряда Лорана содержит бесконечное количество слагаемых.
главная часть ряда Лорана содержит бесконечное количество слагаемых.
Доказательство (ДОК 29). Напомним строение ряда Лорана в окрестности точки  в общем случае:
в общем случае:
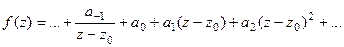
Пункт 1) Если присутствует хотя бы одна отрицательная степень, то 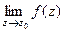 не будет конечным числом. Таким образом, если
не будет конечным числом. Таким образом, если 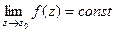 то
то 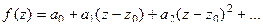 , причём
, причём 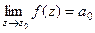 .
.
И обратно, если 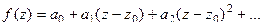 то
то  , потому что
, потому что 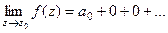 , ведь каждое слагаемое кроме
, ведь каждое слагаемое кроме 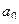 стремится к 0.
стремится к 0.
Пункт 2) Точка  является полюсом порядка m эквивалентно тому, что
является полюсом порядка m эквивалентно тому, что 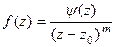 , где функция в числителе имеет ненулевой предел, поэтому её разложение в ряд имеет вид:
, где функция в числителе имеет ненулевой предел, поэтому её разложение в ряд имеет вид: 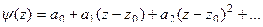
Тогда 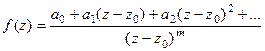 =
=
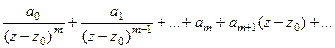 то есть крайняя отрицательная степень это именно число
то есть крайняя отрицательная степень это именно число  если порядок полюса m.
если порядок полюса m.
В главной части может быть не ровно m слагаемых, а какие-то пропущены (коэффициенты 0) но крайнее левое имеет именно степень, равную  .
.
И обратно, если крайняя левая степень  , то можно представить в виде
, то можно представить в виде
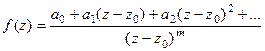 т.е.
т.е. 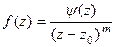 , и тогда точка является полюсом.
, и тогда точка является полюсом.
Пункт 3) Если точка является существенно-особой, но при этом допустить, что главная часть ряда Лорана состоит из нулевого либо из конечного количества слагаемых, то согласно предыдущим пунктам, получали бы противоречие: точка или устранимая, или полюс, и не является существенно-особой. Таким образом, из того, что она существенно-особая, логически следует бесконечность главной части ряда. И обратно, если главная часть бесконечна, то невозможно допустить, что точка полюс или устранимая, иначе сразу получалось бы противоречевое условие, что главная часть конечна.
Пример. Найти все особые точки и указать их тип для 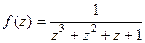 .
.
Решение. Преобразуем знаменатель:  =
=
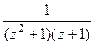 =
= 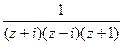 . В знаменателе 3 нуля, причём каждый 1-го порядка, а именно
. В знаменателе 3 нуля, причём каждый 1-го порядка, а именно 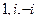 . Следовательно, для функции 3 полюса 1-го порядка:
. Следовательно, для функции 3 полюса 1-го порядка:  .
.
Пример. Указать тип всех особых точек для функции:
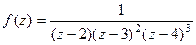 .
.
Решение. В знаментателе нули 1-го, 2-го и 3-го порядка, а именно, точки 2,3 и 4. Тогда для 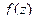 :
: 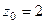 полюс 1-го порядка,
полюс 1-го порядка,
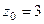 полюс 2-го порядка,
полюс 2-го порядка, 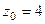 полюс 3-го порядка.
полюс 3-го порядка.
Теорема 3. Если 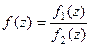 , причём точка
, причём точка  является нулём порядка m для функции
является нулём порядка m для функции  , и нулём порядка n для функции
, и нулём порядка n для функции 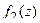 , то при
, то при  точка
точка  устранимая или правильная точка, а при
устранимая или правильная точка, а при 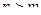 полюс порядка
полюс порядка 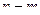 для функции
для функции 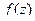 .
.
Доказательство (ДОК 30). Если  - нуль порядка m и n соответственно для числителя и знаменателя, то
- нуль порядка m и n соответственно для числителя и знаменателя, то 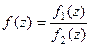 =
= 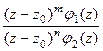 =
= 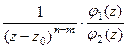 где
где 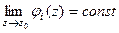 для каждой из двух функций. Тогда можно обозначить
для каждой из двух функций. Тогда можно обозначить  и в итоге
и в итоге  , это и означает, что полюс порядка
, это и означает, что полюс порядка 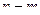 .
.
Пример. Определить тип особой точки 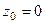 для функции
для функции 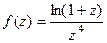 .
.
Решение. Представим функцию в числителе в виде разложения в ряд Тейлора.
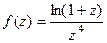 =
= 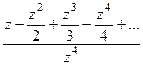 =
=  в числителе нуль 1 порядка, а в знаменателе 4-го. Тогда точка
в числителе нуль 1 порядка, а в знаменателе 4-го. Тогда точка  полюс 3 порядка.
полюс 3 порядка.
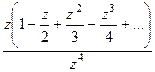 =
=  =
=  . В числителе после сокращения осталась функция, имеющая ненулевой предел.
. В числителе после сокращения осталась функция, имеющая ненулевой предел.
Вычеты
Определение. Пусть 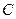 замкнутый контур, внутри него точка
замкнутый контур, внутри него точка  , на самом контуре и внутри него нет особых точек, кроме
, на самом контуре и внутри него нет особых точек, кроме  . Тогда интеграл
. Тогда интеграл 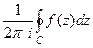 называется вычетом функции
называется вычетом функции 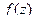 в точке
в точке  и обозначается
и обозначается  .
.
Теорема 1. Вычет функции равен коэффициенту 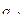 в разложении в ряд Лорана.
в разложении в ряд Лорана. 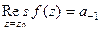 .
.
Доказательство. В § 5 прошлой главы («интегральная формула Коши») доказывали теорему 5 о разложении в ряд Лорана, и получили, в частности, 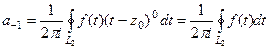 . А правое выражение это и есть вычет.
. А правое выражение это и есть вычет.
Теорема 2. Если  - правильная точка или устранимая особая точка, то
- правильная точка или устранимая особая точка, то 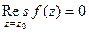 .
.
Доказательство. Если 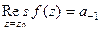 , а для правильной или устранимой особой точки
, а для правильной или устранимой особой точки 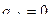 по теореме 2 прошлого параграфа, то
по теореме 2 прошлого параграфа, то 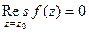 .
.
Теорема 3. Если  простой полюс (т.е. 1-го порядка) то верна формула вычисления вычета:
простой полюс (т.е. 1-го порядка) то верна формула вычисления вычета:  =
= 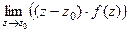 .
.
Доказательство (ДОК 31). Можно доказать двумя методами:
1) с помощью ряда Лорана
2) с помощью интегральной формулы Коши.
Способ 1. Рассмотрим ряд Лорана. Если полюс 1-го порядка, то крайняя отрицательная степень равна 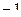 , то есть ряд имеет такой вид:
, то есть ряд имеет такой вид:

Домножим на 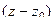 , чтобы выразить крайний коэффициент
, чтобы выразить крайний коэффициент 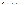 .
.
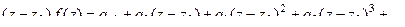
Теперь все слагаемые стремятся к 0 при 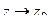 , кроме
, кроме 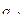 .
.
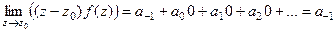 , при этом из теоремы 1 известно, что
, при этом из теоремы 1 известно, что 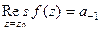 .
.
Тогда  =
= 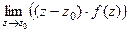 .
.
Способ 2. Если  полюс 1-го порядка, то функцию можно представить в виде:
полюс 1-го порядка, то функцию можно представить в виде: 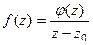 , тогда верно
, тогда верно 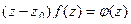 . В то же время по интегральной формуле Коши:
. В то же время по интегральной формуле Коши: 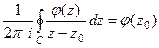 .Тогда
.Тогда 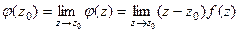 .
.
 =
= 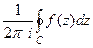 =
=  =
= 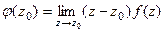 .
.
Что и требовалось доказать.
Оставшиеся лекции:
ЛЕКЦИЯ 13. 28.11.2018 Ряды Фурье
ЛЕКЦИЯ 14. 05.12.2018 Ряды Фурье
Приложение 1. Список доказательств в билеты.
(ДОК 1). Вывести формулу поверхностного интеграла 2 рода:
 =
= 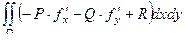 .
.
(ДОК 2) Докажите формулу Грина: 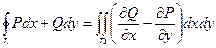 .
.
(ДОК 3) Доказать, что криволинейный интеграл 2 рода не зависит от пути 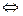 циркуляция по замкнутому контуру равна 0.
циркуляция по замкнутому контуру равна 0.
(ДОК 4) Доказать, что поле F потенциально 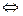 криволинейный интеграл 2 рода от F не зависит от пути.
криволинейный интеграл 2 рода от F не зависит от пути.
(ДОК 5) Доказать, что поле F потенциально 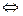 симметрична производная матрица.
симметрична производная матрица.
(ДОК 6) Докажите формулу Остроградского-Гаусса:  .
.
(ДОК 7) Докажите, что  =0,
=0, 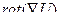 = 0.
= 0.
(ДОК 8).Докажите формулы 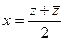 ,
, 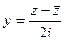
(ДОК 9). Докажите формулу Эйлера  .
.
(ДОК 10) Докажите формулы: 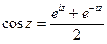 ,
, 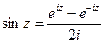 .
.
(ДОК 11) Докажите формулу логарифма  .
.
(ДОК 12). Доказать что линейное отображение 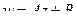 в комплексной плоскости есть композиция растяжения, поворота и сдвига.
в комплексной плоскости есть композиция растяжения, поворота и сдвига.
(ДОК 13). Докажите теорему: Функция 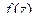 дифференцируема
дифференцируема 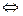
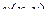 и
и 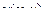 дифференцируемы и выполняются условия Коши-Римана:
дифференцируемы и выполняются условия Коши-Римана: 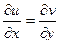 и
и  .
.
(ДОК 14). Докажите, что  дифференцируемая функция
дифференцируемая функция  векторные поля
векторные поля 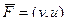 и
и 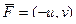 потенциальны.
потенциальны.
(ДОК 15). Если функция является аналитической в некоторой области D, то для каждой из её частей (действительной и мнимой)  в этой области выполняется уравнение Лапласа:
в этой области выполняется уравнение Лапласа:
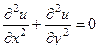 и
и 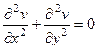 .
.
(ДОК 16). Доказать, что условия Коши-Римана эквивалентны условию  .
.
(ДОК 17). Докажите, что если  замкнутый контур, внутри которого во всех точках
замкнутый контур, внутри которого во всех точках  является аналитической, то
является аналитической, то  .
.
(ДОК 18). Докажите, что если 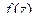 является аналитической во всех точках некоторой области
является аналитической во всех точках некоторой области  , граница которой односвязна, то интеграл от функции
, граница которой односвязна, то интеграл от функции 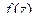 не зависит от пути, то есть имеет одно и то же значение для любой кривой
не зависит от пути, то есть имеет одно и то же значение для любой кривой  , соединяющей пару точек
, соединяющей пару точек  .
.
(ДОК 19). Докажите, что функция 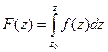 является первообразной от функции
является первообразной от функции 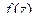 .
.
(ДОК 20). Докажите, что для аналитической на кривой  функции верна формула Ньютона-Лейбница:
функции верна формула Ньютона-Лейбница:  .
.
(ДОК 21). Доказать интегральную теорему Коши о том, что 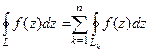 .
.
(ДОК 22). Доказать интегральную формулу Коши: 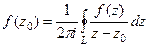
(ДОК 23). Доказать обобщённую интегральную формулу Коши: 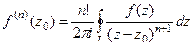 .
.
(ДОК 24). Доказать теорему о разложении функции в ряд Тейлора.
(ДОК 25). Доказать теорему о разложении функции в ряд Лорана.
(ДОК 26). Доказать, что не существует числовой системы нечётной размерности без делителей нуля.
(ДОК 27). Доказать теорему о виде ряда Тейлора в окрестности нуля порядка m.
(ДОК 28). Доказать теорему об изолированности нулей.
(ДОК 29). Теорема о взаимосвязи типа особой точки и строения ряда Лорана.
(ДОК 30). Доказать теорему: Если  , причём точка
, причём точка 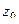 является нулём порядка m для функции
является нулём порядка m для функции  , и нулём порядка n для функции
, и нулём порядка n для функции  , то при
, то при 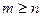 точка
точка 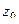 устранимая или правильная точка, а при
устранимая или правильная точка, а при  полюс порядка
полюс порядка 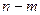 для функции
для функции 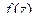 .
.
(ДОК 31). Доказать формулу вычисления вычета для полюса 1-го порядка:  =
= 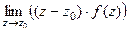 .
.
(ДОК 32). Доказать, что если функция имеет вид  , где
, где 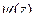 имеет нуль 1 порядка в точке
имеет нуль 1 порядка в точке 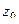 , а
, а 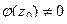 , то
, то 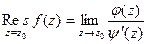 .
.
(ДОК 33). Доказать, что если 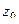 - полюс порядка m, то верна
- полюс порядка m, то верна
 =
=  .
.
(ДОК 34). Доказать, что если  устранимая особая точка, то:
устранимая особая точка, то:
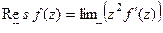
(ДОК 35). Доказать, что если 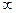 является полюсом порядка m, то:
является полюсом порядка m, то:
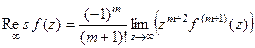
(ДОК 36). Доказать, что  .
.
(ДОК 37). Доказать, что 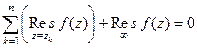 .
.
Приходовский М.А.
Математика
Курс лекций
Семестр 3
Учебное пособие
Для специальности
информатика и вычислительная техника»
Томск
ТУСУР
2018
Электронное учебное пособие составлено и скорректировано с учётом реального проведения лекций на ФСУ в группах 437-1,2,3 осенью 2018 года.
(ДОК №) - доказательства формул или теорем, которые попадают в теооретические билеты.
Оглавление
| Глава 1. Криволинейные и поверхностные интегралы, теория поля...................................................................................... § 1. Криволинейные и поверхностные интегралы 1 рода............ § 2. Криволинейные и поверхностные интегралы 2 рода............ § 3. Элементы теории поля.............................................................. Глава 2. Теория функций комплексного переменного ........... § 1. Действия с комплексными числами......................................... § 2. Функции комплексного переменного...................................... § 3. Дифференцирование комплексных функций......................... § 4. Интегрирование комплексных функций................................. § 5. Интегральная формула Коши .................................................. § 6. Комплексные числа и дифференциальные уравнения.......... § 7. Гиперкомплексные числовые системы. Кватернионы......... Глава 3. Особые точки и вычеты ............................................. § 1. Нули аналитической функции............................................... § 2. Особые точки .......................................................................... § 3. Вычеты..................................................................................... § 4. Приложения вычетов.............................................................. Глава 4. Ряды Фурье .................................................................... | 5 5 10 17 33 33 35 41 50 58 70 71 76 76 77 84 |
Оглавление по номерам лекций
| Лекция 1.......................................................................................... Лекция 2.......................................................................................... Лекция 3.......................................................................................... Лекция 4.......................................................................................... Лекция 5.......................................................................................... Лекция 6.......................................................................................... Лекция 7.......................................................................................... Лекция 8.......................................................................................... Лекция 9.......................................................................................... Лекция 10......................................................................................... Лекция 11......................................................................................... Лекция 12......................................................................................... Лекция 13......................................................................................... Лекция 14......................................................................................... Лекция 15......................................................................................... Лекция 16......................................................................................... | 5 13 21 32 41 50 58 69 77 86 |
ЛЕКЦИЯ 1. 05.09.2018
Глава 1.
Дата: 2018-12-21, просмотров: 374.