Рассылка.

Во многих параллельных алгоритмах возникает потребность одно данное разослать сразу во много вычислительных устройств. Такая операция рассылки обычно в языках программирования называется broadcast. Иногда рассылка поддерживается аппаратно (если, например, вычислительные устройства соединены коммуникационной сетью «звезда»). 

Кольцевой сдвиг.

Кольцевая сеть позволяет одновременно выполнять пересылки, соответствующие только циклическим сдвигам, т. е. таким подстановкам s, что для любых i,jÎ{1,..,p} (s_i-i) mod p = (s_j - j) mod p. Например,

S =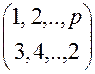

Время на пересылку данных в соответствии с такой подстановкой s на полнодоступном коммутаторе есть величина T0, не зависящая от p и от того, какое данное в каком ПЭ расположено (лишь бы не требовалось в один момент времени считывать (или записывать) несколько данных из памяти одного ПЭ). С другой стороны, время для пересылки данных на кольцевой сети равно T1+T2*|s_i - i|, где i – номер ПЭ, из которого данное считывается, s_i – номер ПЭ, в который данное записывается, T1, T2 - константы, не зависящие от p и размещения данных. Здесь, конечно, предполагается, что для всех i=1,...,p пересылки могут быть выполнены одновременно, если (s_i -i) mod p не зависит от i. Константа T1 означает время загрузки данных из процессорного элемента, пересылающего данные, в коммуникационную сеть, плюс время считывания из коммуникационной сети в процессорный элемент, получающий данные. Константа T2 означает время движения данных по коммуникационной сети между двумя соседними процессорными элементами (исключая время загрузки-выгрузки данных).

Транспонирование.

       Есть разные стандарты представления двумерной матрицы в одномерной памяти компьютера. Трансляторы языка ФОРТРАН размещают матрицы «по столбцам», а трансляторы языка Си – «по строкам». От способа размещения матрицы может зависеть время работы программы. Если при обращении к матрице считываются ее столбцы, то удобнее, чтобы элементы этих столбцов находились в памяти рядом – в этом случае и происходит лучшее попадание в кэш-линейку и быстрее вычисление адреса следующего элемента массива (прибавление единицы). Если в программе обращение к матрице по строкам – то и размещать матрицу лучше, соответственно, по строкам. Но может так случиться, что в одном месте программы есть обращение к матрице по строкам, а в другом месте – по столбцам, причем и тех и других обращений много. Тогда бывает эффективным переразмещение матрицы – транспонирование. Транспонирование матрицы представляет собой такое переразмещение массива в памяти компьютера, при котором строки размещаются, как столбцы, а столбцы – как строки. Если компилятор все массивы размещает одинаково либо по строкам, либо по столбцам, то транспонирование может быть описано простой программой

DO 1 I₁ = 0, N-1

DO 1 I₂ = 0, N-1

 1 Y(I₁,I₂) = X(I₂,I₁)

       В данном случае в памяти компьютера кроме исходной матрицы X будет существовать и транспонированная к ней матрица Y. Несложно записать программу, в которой транспонированная матрица займет место исходной

DO 1 I₁ = 0, N-1

DO 1 I₂ = 0, I₁

T = X(I₂,I₁)

X(I₂,I₁) = X(I₁,I₂)

 1    X(I₁,I₂) = T

Транспонирование матриц использовалось в традиционных последовательных компьютерах для более быстрого обращения к памяти.

       Общий параллельный алгоритм переразмещения массивов и, в частности, транспонирования будет описан далее.

Скашивание.

Матрица-клетка – это матрица, размерность которой равна количеству модулей памяти. Во многих эффективных параллельных алгоритмах (для архитектуры SIMD [81]) произвольные матрицы могут быть представлены как блочные матрицы, блоки которых – матрицы-клетки. Скошенная форма хранения матрицы-клетки – это такое размещение матрицы, при котором в каждом модуле памяти хранится некоторая косая диагональ матрицы.

 a₁₁ a₁₂ a₁₃ a₁₄          

 a₂₁ a₂₂ a₂₃ a₂₄          

 a₃₁ a₃₂ a₃₃ a₃₄          

 a₄₁ a₄₂ a₄₃ a₄₄          

       Рис. 51. Косые диагонали матрицы.

      P₁ P₂ P₃ P₄   

 a₁₄ a₁₁ a₁₂ a₁₃          

 a₂₃ a₂₄ a₂₁ a₂₂           

 a₃₂ a₃₃ a₃₄ a₃₁           

 a₄₁ a₄₂ a₄₃ a₄₄          

       Рис. 52. Скошенное размещение матрицы в параллельной памяти. Над столбцами обозначены номера процессоров, в которых эти столбцы размещены.

Скошенная форма хранения позволяет обращаться одновременно как к элементам любой строки матрицы-клетки, так и к элементам любого столбца. Алгоритм приведения матрицы к скошенной форме может выглядеть следующим образом.

DO 1 I₁ = 0, p

DO 1 I₂ = 0, p

 1 Y(I₁,I₂) = X( (I₂ + I₁) mod p , I₁)

Задачи.

Задача 1. Как разместить матрицу  N*N в распределенной памяти так, чтобы ее транспонирование занимало малое время, если в качестве коммуникационной сети используется кольцо:

1. В ПЭ с номером k строка с номером k (mod p)
2. В ПЭ с номером k столбец с номером k (mod p)
3. В ПЭ с номером k полоса строк с номерами от (N/p)*(k-1)  до (N/p)*k
4. В ПЭ с номером k столбцов с номерами  (N/p)*(k-1) до (N/p)*k
5. В ПЭ с номером k блок с номерами строк (N/p^0.5)*(i-1) до (N/p^0.5)*i  и с номерами столбцов (N/p^0.5)*(j-1) до (N/p^0.5)*j ; i = k div p^0.5 ; j = k mod p^0.5 .  

Задача 2. В параллельной вычислительной системе в качестве коммуникационной сети используется двумерная квадратная решетка (тор). Узлы пронумерованы от 0 до (p-1) сверху-вниз, слева-направо. Как разместить матрицу N*N в распределенной памяти так, чтобы ее транспонирование занимало малое время:

1. В ПЭ с номером k строка с номером k (mod p)
2. В ПЭ с номером k столбец с номером k (mod p)
3. В ПЭ с номером k полоса строк с номерами от (N/p)*(k-1) до (N/p)*k
4. В ПЭ с номером k столбцов с номерами (N/p)*(k-1) до (N/p)*k
5. В ПЭ с номером k блок с номерами строк (N/p^0.5)*(i-1) до (N/p^0.5)*i и с номерами столбцов (N/p^0.5)*(j-1) до (N/p^0.5)*j ; i = k div p^0.5 ; j = k mod p^0.5 .

Задача 3. В параллельной вычислительной системе в качестве коммуникационной сети используется n-мерный куб. Узлы имеют стандартную для гиперкуба двоичную кодировку, которая может быть переведена в десятичную с нумерацией от 0 до (p-1), p=2ⁿ. Как разместить матрицу N*N в распределенной памяти так, чтобы ее транспонирование занимало малое время:

1. В ПЭ с номером k строка с номером k (mod p)
2. В ПЭ с номером k столбец с номером k (mod p)
3. В ПЭ с номером k полоса строк с номерами от (N/p)*(k-1) до (N/p)*k
4. В ПЭ с номером k столбцов с номерами (N/p)*(k-1) до (N/p)*k
5. В ПЭ с номером k блок с номерами строк (N/p^0.5)*(i-1) до (N/p^0.5)*i и с номерами столбцов (N/p^0.5)*(j-1) до (N/p^0.5)*j ; i = k div p^0.5 ; j = k mod p^0.5 .