Важными характеристиками архитектуры являются виды используемой памяти: регистровая, кэш, оперативная, внешняя, распределенная, глобально адресуемая, общая, общая распределенная, иерархическая, ортогональная. В данной работе будут рассматриваться общая, распределенная и общая распределенная виды памяти.

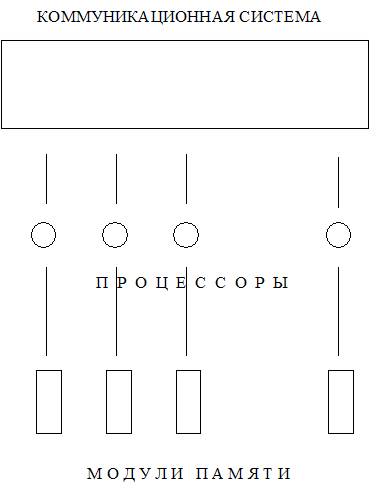
       Рис. 2. Многопроцессорная система с распределенной памятью.

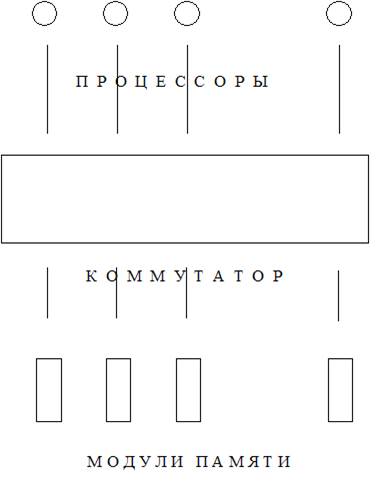
       Рис. 3. Многопроцессорная система с общей распределенной памятью.

       Будем использовать термин «параллельная память», понимая под этим одно из двух: либо распределенную память, либо общую распределенную. Неформально говоря, параллельная память означает возможность одновременного доступа к нескольким данным. Размещение данных в параллельной памяти – нетривиальная задача, существенно влияющая на быстродействие программы. 

       Более подробные описания некоторых параллельных вычислительных архитектур можно найти в [138], [66], [81].

       SIMD. Архитектура SIMD (Single Instruction Multiple Data) допускает выполнение одновременно несколько одинаковых операций над различными данными. Примерами компьютеров с такой архитектурой являются ILLIAK-4, Connection Machine2 и отечественный суперкомпьютер ПС-2000 [81] и др. [136]. Несмотря на жесткость ограничений, на эту архитектуру эффективно отображается достаточно представительный класс алгоритмов, имеющих регулярную структуру: задачи линейной алгебры с заполненными матрицами, сеточные методы решения уравнений математической физики в прямоугольных областях, быстрое преобразование Фурье и некоторые другие [81]. Архитектура SIMD синхронная, поскольку все процессоры в каждый момент выполняют одинаковые операции. К классу архитектур SIMD можно отнести и векторные архитектуры (пример векторного компьютера – Cray1).

       MIMD. Архитектура MIMD (Many Instructions Multiple Data) – «много команд – много данных». К этому классу параллельных компьютеров можно отнести мультитранспьютерные системы, суперкомпьютер ПС-3000, самый мощный российский суперкомпьютер «Ломоносов» (размещается в МГУ), кластерные системы и массово-параллельные суперкомпьютеры с распределенной памятью [70]. Архитектура MIMD асинхронная. Каждый процессор суперкомпьютера такой архитектуры может работать по своей индивидуальной программе. Возникают проблемы с синхронизацией работы процессоров, которая необходима при обращениях к общим данным.

Векторные и матричные компьютеры. Векторные компьютеры ориентированы на эффективные операции над векторами. К векторным компьютерам можно отнести Cray1, ПС-3000, суперкомпьютеры японской фирмы NEC. Векторные компьютеры, как правило, имеют общую память. Эти компьютеры синхронные и допускают эффективное автоматическое распараллеливание (векторизацию) для достаточно представительного класса программ. Поддержка векторных операций реализована на некоторых современных массовых процессорах (Intel). Автоматическое выделение векторных команд рассмотрено, например, в [30], [20].

Матричные компьютеры – это, обычно, приставки к некоторой управляющей машине. Матричные компьютеры представляют собой прямоугольную (как правило, квадратную) матрицу процессоров. Такие архитектуры просты в реализации. Узкие места – обмен данными и командами с управляющей машиной и обмены между процессорами.

Конвейерные вычислители. Вычислительный конвейер (PIPELINE) – это такая совокупность устройств, что выходы одних связаны непосредственно с входами других [111], [66]. Конвейерное соединение устройств позволяет экономить время на обращениях к памяти. Конвейеры могут использоваться на разных уровнях вычислений. Например, побитовый конвейер может вычислять произведение двух чисел. А суперкомпьютер ПС-2100 допускал режим работы, при котором в конвейер соединялись десять 64-процессорных модулей. Конвейер эффективен при большом потоке однотипных вычислений, загружающих все устройства конвейера. Жесткое соединение устройств, входящих в конвейер, предполагает, что конвейер будет вычислять только одну функцию (или несколько функций с близкими алгоритмами). Это ограничивает применение конвейеров. Много работ посвящено эффективному отображению фрагментов программ на конвейерные системы, причем эти же алгоритмы оказываются применимы и к программному конвейеру, который организуется на суперкомпьютерах с архитектурой очень длинного командного слова [111], [89], [134], [133]. В последнее время много вычислительных устройств разрабатывается на ПЛИС – программируемых логических интегральных схемах [86]. Многоконвейерные модели вычислений рассматривались в [109], [84], [50].

Возникает проблема синхронизации вычислительных устройств в конвейере. Действительно, если первое устройство будет генерировать данные быстрее, чем второе сможет их обрабатывать, то некоторые данные будут пропадать необработанными. Если же первое устройство будет работать медленнее второго, то второе будет брать из памяти случайные данные (предыдущие), что приведет к неверным вычислениям.

Для синхронизации конвейерных вычислений к быстрым вычислительным устройствам добавляются задержки, после чего все вычислительные устройства работают с одинаковой скоростью. Конвейерные вычисления могут быть организованы на уровне микрокоманд, на уровне арифметических операций и (крупные конвейеры) на уровне процессов.

Конвейерные вычислители могут брать данные, как из общей памяти, так и из общей распределенной.

Конвейеры удобны при наличии потока однотипных вычислений. В этом случае все устройства конвейера загружены. Пока одни данные завершают обработку в последнем ВУ конвейера, другие данные в это же время обрабатываются на первых ВУ конвейера. Благодаря такой организации вычислений осуществляется параллелизм в работе вычислительных устройств, составляющих конвейер.

Конвейерные вычислители широко применяются при цифровой обработке сигналов (обработка потока сигналов). В процессорах Pentium для вычисления циклов (если достаточно регистров) используется так называемый программный конвейер (software pipeline), который представляет собой временно (на время вычисления цикла) зафиксированную последовательность регистров, обрабатывающих данные.

Работа вычислительного конвейера подобна работе промышленного конвейера, например, конвейера швейной фабрики, выпускающего джинсовые брюки с карманами и заклепками.

       Рис. 4. Несинхронизированный конвейер.

Первый станок конвейера, изображенного на рисунке, сшивает джинсы из частей ткани (за 10 минут), второй станок – пришивает карманы (15 минут), а третий – ставит заклепки (5 минут). Корзина (буфер), в которую попадает продукция, выходящая с первого станка, и, из которой ее берет работница, обслуживающая второй станок (для пришивания карманов), будет постепенно заполняться и со временем может переполниться. Третий станок треть рабочего времени будет простаивать. Процессы этого конвейера не синхронизированы. 

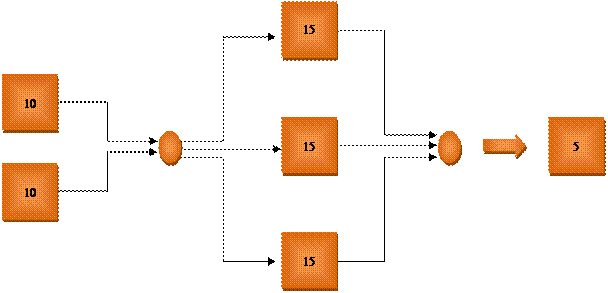
       Рис. 5. Синхронизированный конвейер.

Если установить рядом 2 станка первого типа (сшивающих раскроенные части ткани), 3 станка второго типа (пришивающих карманы) и оставить один станок третьего типа (ставящий заклепки) – то все станки будут загружены равномерно, никакие корзины (буферы) между станками переполняться не будут, каждые 30 минут будет с конвейера выпускаться по 6 джинсов.

Для синхронизации вычислительного конвейера тоже можно ставить по нескольку параллельно работающих элементарных процессора (сумматоров, умножителей…), но чаще ставят буферы для задержки подаваемых данных, этим самым удлиняя время выполнения коротких операций так, чтобы сравнять это время со временем выполнения самой долгой операции.

Задача. Пусть конвейер состоит из 3 этапов по a, b и c минут выполнения (a, b, c – натуральные числа). Сколько нужно поставить параллельно работающих станков 1 типа, второго типа и третьего типа?

Варианты ответов:

1. a/НОД(a,b,c), b/НОД(a,b,c), c/НОД(a,b,c)

2. НОК(a,b,c)/a, НОК(a,b,c)/b, НОК(a,b,c)/c

3. bc, ac, ab

4. НОД(b,c), НОД(a,c), НОД(a,b)

5. НОК(b,c), НОК(a,c), НОК(a,b)