Будем рассматривать компьютер с N вычисляющими устройствами (процессорами) и N модулями памяти. Будем считать, что для любой перестановки s из N элементов коммуникационное устройство (коммутатор) компьютера позволяет одновременно организовать N соединений: каждый процессор с номером i соединяется с модулем памяти, имеющим номер si .
Одним из наиболее интересных американских суперкомпьютеров с разделяемой параллельной памятью был компьютер RP-3 фирмы IBM [112]. В работах [48], [73] описана архитектура суперкомпьютеров, в которой имеется распределенная совместно используемая (разделяемая) память и поле процессоров, из которых с помощью коммутатора может собираться конвейер любой конфигурации (в частности, несколько конвейеров).
Вычислительная система с разделяемой памятью состоит из множества модулей памяти, множества элементарных процессоров и коммутатора. Процессоры не имеют своей локальной памяти. Допускается в один момент времени обращаться к разным модулям памяти (для чтения или записи).
Из каждого модуля памяти и из каждого процессора есть выход, ведущий на вход коммутатора. К каждому модулю памяти и к каждому входу каждого процессора ведет какой-нибудь выход коммутатора. Будем считать, что коммутатор обладает свойством полнодоступности, т.е. позволяет соединять входы и выходы в любых необходимых комбинациях. Более строго, если у коммутатора N входов и N выходов, то для любой перестановки s из N чисел коммутатор позволяет одновременно соединить для каждого i = 1, ..., N каждый вход с номером i с выходом с номером si . Такие коммутаторы описаны, например, в [6], [15].
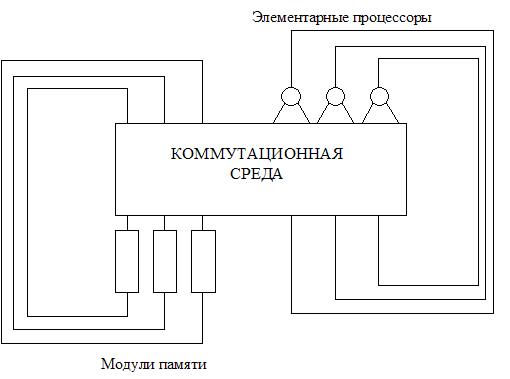
Рис. 6. Схема коммутации процессоров и модулей памяти.
VLIW. Суперкомпьютеры VLIW (Very Long Instruction Word) – с очень длинным командным словом, допускают одновременное выполнение набора простых команд. Простыми командами в данном случае могут быть арифметические операции, нормализация вещественных чисел с плавающей запятой, считывание данных из памяти,… Такие компьютеры распараллеливают линейные участки программ, т.е. фрагменты программ, состоящие только из операторов присваивания. На основе анализа требований к языкам программирования формировалась архитектура суперкомпьютера «Эльбрус» [12], [13], [14]. Автоматическая оптимизация программ на такие архитектуры рассматривалась в [29].
Симметрические и многоядерные архитектуры. В симметрических архитектурах SMP несколько процессоров размещаются на общей памяти. Симметрические архитектуры асинхронны и используются в качестве серверов. Многоядерные процессоры – это процессоры, в которых на одном кристалле размещается несколько ядер, каждое из которых эквивалентно самостоятельному универсальному процессору предыдущих поколений. Ядра такого процессора работают асинхронно и используют общую память. И симметрические, и многоядерные процессоры используют принципы многопоточного программирования [113].
Гибридные архитектуры. В вычислительных системах иногда используются комбинации нескольких архитектурных принципов. Например, в последнее время часто создаются кластеры из компьютеров с многоядерными процессорами или из SMP компьютеров. В результате получается, что множество вычислительных устройств разбито на группы, каждая из которых имеет свой модуль памяти, доступ к которому намного эффективнее, чем к модулю памяти другой группы. Такие системы относят к классу NUMA (Non-Uniform Memory Access).
GRID. Грид – это несколько кластеров, объединенных по глобальной сети. В грид могут входить несколько сотен компьютеров. Алгоритмы вычисления на грид должны быть устойчивы к отключению каких-либо компьютеров в сети. Эффективно на грид могут решаться задачи, которые распадаются на большое количество слабо связанных друг с другом подзадач.
Вычислители с программируемой архитектурой. Всякая параллельная вычислительная архитектура не является универсальной. Программируемые (или перестраиваемые) архитектуры обладают возможностью относительных изменений. Чаще всего перенастраиваются только связи между устройствами вычислительной системы. Идея программируемых (перестраиваемых) архитектур состоит в том, что не алгоритм решения задачи адаптируется к архитектуре, а, наоборот, вычислительная архитектура адаптируется к алгоритму решения задачи. Модели вычислительных систем с программируемой архитектурой обсуждаются несколько десятилетий. Здесь можно отметить отечественные работы Э.В. Евреинова, В.Г. Хорошевского, А.В. Каляева, В.В. Корнеева: [58] [64], [65], [59], [46], [49]. Но реализации вычислительных систем с программируемой архитектурой появились только в последние годы на основе ПЛИС-технологий. Наиболее успешными оказались системы с архитектурой перестраиваемого конвейера [115], [116], [117], [72], [50].
Современные проекты вычислительных архитектур. Основная тенденция первого десятилетия 21-ого века в повышении производительности компьютеров – это увеличение параллелизма на одном кристалле (в предыдущем десятилетии повышалась тактовая частота). В первую очередь здесь следует отметить многоядерные процессоры (фирмы Intel, IBM, AMD). Количество ядер на одном кристалле предполагается довести до 256. На основе однокристального параллелизма в США развиваются наиболее высокопроизводительные проекты TRIPS и Blue Gene, в которых помимо параллелизма на одном кристалле развивается работа с памятью. В России также есть проекты новых высокопроизводительных архитектур. Здесь следует отметить проект однокристального параллельного процессора с программируемой архитектурой [59], [58]. Над новыми процессорами и основанными на них вычислительными комплексами работает группа компаний «Эльбрус» [12].
КОММУНМКАЦИОННЫЕ СИСТЕМЫ
Коммуникационные сети.
Коммуникационные сети связывают элементы вычислительных систем для обмена командами и данными. В частности, такие сети используются для соединения процессорных элементов многопроцессорных вычислительных систем. Такие сети классифицируются в первую очередь по топологическим характеристикам: звезда, иерархическая сеть (дерево), шина и кольцевая шина, решетка, многокольцевое соединение, N-мерный куб, графы малого диаметра (или графы с сильной симметрией, или графы Мура).
Интерес представляют топологические характеристики коммуникационных сетей: диаметр, степень вершин, количество вершин, симметрия.
Диаметр – это величина самого длинного пути в графе. Эта характеристика показывает наибольший путь, который могут проходить данные при коммуникационном обмене.
Многие сети обладают свойством: каждое вычислительное устройство связано с одним и тем же количеством других вычислительных устройств. Граф таких соединений является однородным. Степень однородности (количество связей каждой вершины) – другой важный показатель сети.
Количество вершин (узлов) коммуникационной сети – характеристика, конфликтующая с двумя предыдущими. Ясно, что при малом диаметре и малой степени однородности много вершин в сети быть не может.
Количество связей коммуникационной сети – это один из основных показателей стоимости сети. Этот показатель удовлетворяет следующей формуле:
2 * (Количество связей) = Сумма степеней всех вершин.
Для однородных графов эта формула принимает вид:
2 * (Количество связей) = (Количество вершин) * (Степень однородности)
Еще одно качество коммуникационной сети – наличие симметрии.
Будем говорить, что граф обладает сильной симметрией, если для любых двух вершин этого графа существует такой автоморфизм, который переводит первую вершину во вторую.
По топологиям коммуникационных сетей следует отметить обзор [138] и статью [136].
Звезда и дерево.
Тип соединения компьютеров «звезда» предполагает, что один из компьютеров головной, а каждый из остальных – подчиненных – с ним непосредственно соединен.
Иерархическое соединение предполагает, что к головному компьютеру подсоединены подчиненные первого уровня, к каждому из которых подсоединены компьютеры второго уровня подчинения, и т.д.
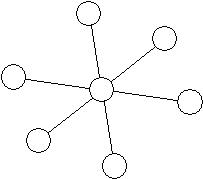
Рис. 7. Соединение звездой.
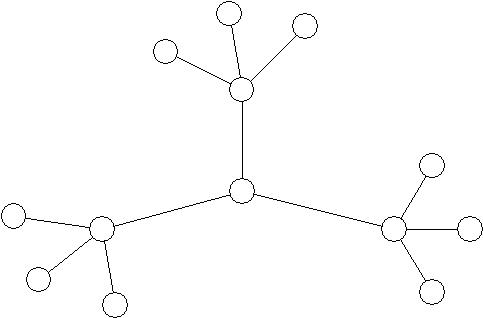
Рис. 8. Иерархическое (древовидное) соединение.
Очевидно, звездные и иерархические сети не являются однородными и не обладают сильной симметрией. Диаметр звезды равен 2. Диаметр иерархического дерева равен числу 2, умноженному на глубину дерева (наибольшее расстояние от корня до висячей вершины). Количество связей звезды и иерархической сети равно количеству вершин минус 1.
Шина и кольцевая шина.
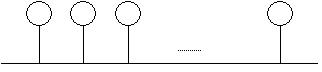
Рис. 9. Шина, соединяющая процессорные элементы
По шине, как и в сети типа «звезда», в один момент времени можно пересылать данные только между двумя узлами (процессорными элементами).
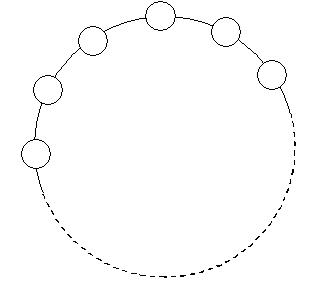
Рис. 10. Многопроцессорная система с кольцевой шиной
Кольцевая сеть бывает однонаправленной и двунаправленной. Однонаправленное кольцо позволяет пересылать данные только в одну сторону. Двунаправленное кольцо – в обе стороны.
Однонаправленная кольцевая сеть имеет диаметр, равный количеству вершин. Двунаправленная кольцевая сеть имеет диаметр, равный половине от количества всех процессорных элементов. И та, и другая кольцевая сеть обладает сильной симметрией. Количество ребер равно количеству вершин.
В суперкомпьютере ПС-2000 использовалась двунаправленная кольцевая сеть.
Решетка и тор.
Многомерная решетка (mesh) – это коммуникационная сеть, вершины которой расположены в узлах многомерной целочисленной решетки, а связи параллельны координатным осям и соединяют соседние узлы по координатным направлениям.
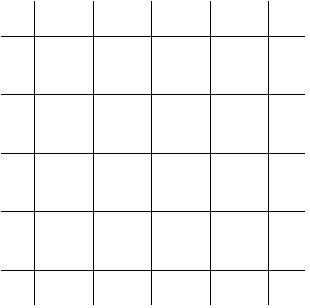
Рис. 11. Двумерная решетка.
Поскольку рассматривается не бесконечная решетка, а лишь ограниченная ее область, вершины, находящиеся на границе, попарно связываются между собой.
Частный случай многомерной решетки – тор – это решетка, у которой противоположные (симметричные относительно координатного подпространства) граничные узлы соединяются между собой.
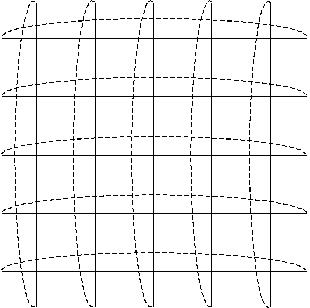
Рис. 12. Двумерный тор.
Диаметр m-мерной решетки размера N = n1 * n2 *…* nm равен (n1 + n2 +…+ nm), а тора – (n1 + n2 +…+ nm) / 2m . Если все стороны решетки равны, то при количестве вершин N диаметр m-мерной решетки равен m * N1/m , а тора – m * N1/m / 2m.
Нетрудно заметить, что при m=1 m-мерная решетка оказывается кольцом.
Многокольцевое соединение.
У кольцевой шины очень большой диаметр. Чтобы его сократить (и этим самым сократить время пересылок данных), можно соединить процессорные элементы еще одним кольцом (или несколькими кольцами). Занумеруем вершины первого кольца в порядке их следования (например, по часовой стрелке). Ввиду естественных требований регулярности (симметрии) второе кольцо должно соединять вершины, разность номеров между которыми постоянна (по модулю количества всех вершин N).
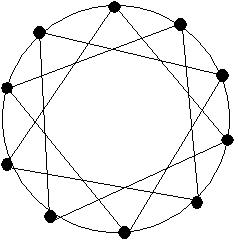
Рис. 13. Двойное кольцевое соединение.
Если количество всех вершин делится на разность номеров вершин, соединяемых вторым кольцом, то полученное двойное кольцо изоморфно тору.
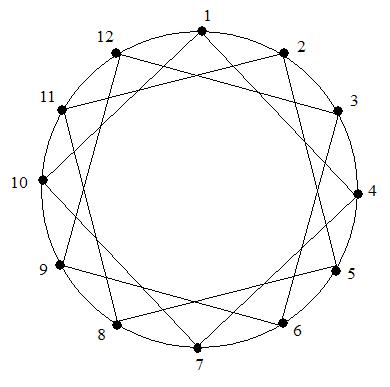
Рис. 14. Двойное кольцо, изоморфное решетке.
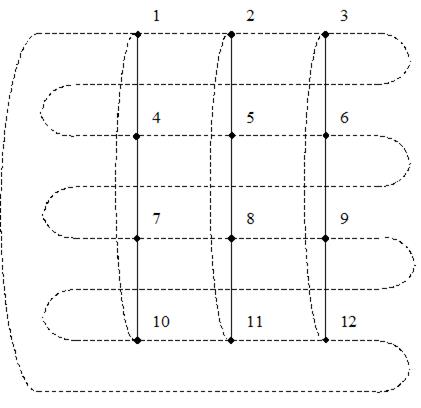
Рис. 15. Решетка, изоморфная двойному кольцу.
Многокольцевая сеть является однородным сильно симметричным графом.
Пусть имеется сеть с m кольцами. Пусть ki – разность номеров вершин, которые соединяются i-ым кольцом, i = 1, 2, …, m. В частности, k1 = 1.
Рассмотрим расстояние от вершины с номером 0 до вершины с номером w однонаправленной многокольцевой сети. Сначала следует двигаться по кольцу с наибольшей разностью номеров (поскольку малое число таких ребер покроют большое расстояние). Количество ребер наибольшего кольца равно w div km (здесь div – целочисленное деление). Остается разность номеров вершин, равную w mod km , покрыть путем по первым m-1 кольцам. По второму по величине кольцу пройдем по (w mod km ) div km-1 ребрам. И т.д.
w div km + (w mod km ) div km-1 + … ≤
w div km + ( km – 1) div km-1 + ( km-1 – 1) div km-2 + …
Если в сети количество вершин равно N, то диаметр однонаправленной сети равен
d = [N/km] + [(km – 1)/km-1] + [(km-1 – 1)/km-2] + … + [(k2 – 1)/k1]
Для двунаправленной сети
d = 1/2m * ([N/km] + [(km – 1)/km-1] + [(km-1 – 1)/km-2] + … + [(k2 – 1)/k1])
Интересен вопрос, при каких значениях чисел k1 , k2 , …, km диаметр достигает наименьшего значения. Следует отметить, что величина d отличается от функции
f = 1/2m * (N/km + km/km-1 +km-1/km-2 + … + k2/k1)
на величину, не превосходящую m, которая, как правило, пренебрежимо мала по сравнению с N. Минимум функции f достигается при равенстве всех чисел N/km = km/km-1 = km-1/km-2 = … = k2/k1 = k и N = km (это можно доказать с помощью неравенства о среднем арифметическом и среднем геометрическом или приравняв к нулю все частные производные этой функции). Оптимальная разность между номерами вершин у кольца с номером s равна Ns/m .
Диаметр в этом случае равен, как и у тора, m * N1/m .
В случае двунаправленного кольца m * N1/m / 2m .
Итак, многомерный тор является частным случаем многокольцевой сети. Но наименьший диаметр многокольцевой сети достигается на торе, который представляет собой декартово произведение одинаковых окружностей.
N-мерный куб.
Гиперкуб – это сеть, граф которой представляет собой n-мерный куб. Вершинам этого графа можно поставить в соответствие булевы векторы длины n. Две вершины соединяются ребром, если соответствующие им векторы отличаются лишь в одной координате. Количество вершин у n-мерного куба равно p=2n. Максимальное расстояние (теоретико-графовое) между вершинами равно n (т.е. логарифм двоичный от количества вершин).
Соединение по топологии n-мерного куба взято за основу в семействе суперкомпьютеров n-Cube. Процессорные элементы располагаются в вершинах n-мерного куба. N-мерный куб – это множество точек (x1 , x2 , … , xn) n-мерного пространства, удовлетворяющих условию 0 ≤ x1 ≤ 1, 0 ≤ x2 ≤ 1, … , 0 ≤ xn ≤ 1 .

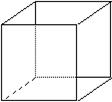
Рис. 16. Двумерный и трехмерный кубы.
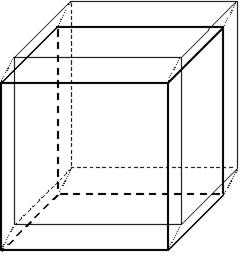
Рис. 17 Четырехмерный куб.
Степени всех вершин n-мерного куба одинаковы и равны n . Вершины n-мерного куба помечаются векторами координат в n-мерном пространстве. Поскольку куб единичный, эти векторы являются битовыми. Одномерные ребра n-мерного куба соединяют вершины, коды которых отличаются только в одной координате.
Описанная кодировка вершин дает простой алгоритм поиска пути от одной вершины к другой. Пусть даны две вершины n-мерного куба и их битовые кодировки. Находим первую координату, в которой отличаются кодировки вершин. Из первой вершины переходим в смежную по ребру, соответствующему этой координате. Далее – рекурсивно.
Пример 2. Опишем путь из вершины A=(1,1,0,1,0,0) в вершину B=(1,0,0,1,1,0). Первая несовпадающая координата – 2. Поэтому перейдем из вершины A в вершину A2 = (1,0,0,1,0,0) по ребру 0 ≤ x2 ≤ 1. Между кодировками вершин A2 и B несовпадающая координата 5. Поэтому из вершины A2 в вершину B переход по ребру 0 ≤ x5 ≤ 1 .
Графы малого диаметра.
Графы малого диаметра – это однородные графы с фиксированным диаметром и наибольшим количеством вершин. Графы малого диаметра – это несколько более широкий класс графов, чем активно исследовавшиеся графы с сильной симметрией [4], [7], [64], [65].
Графы малого диаметра интересны в качестве использования для топологии коммуникационных сетей, поскольку при большом количестве узлов наибольшее расстояние между узлами в таких графах невелико.
Интересной представляется задача построения однородных графов с фиксированным диаметром и максимальным количеством вершин. Решетка и многокольцевая сеть не являются графами с оптимальным количеством вершин при фиксированных степени однородности и диаметре. Например, четырехмерный куб – это граф однородный степени 4 диаметра 4 с 16 вершинами. На следующем рисунке изображен граф однородный степени 4 диаметра 3 с 17 вершинами (этот граф не обладает сильной симметрией).
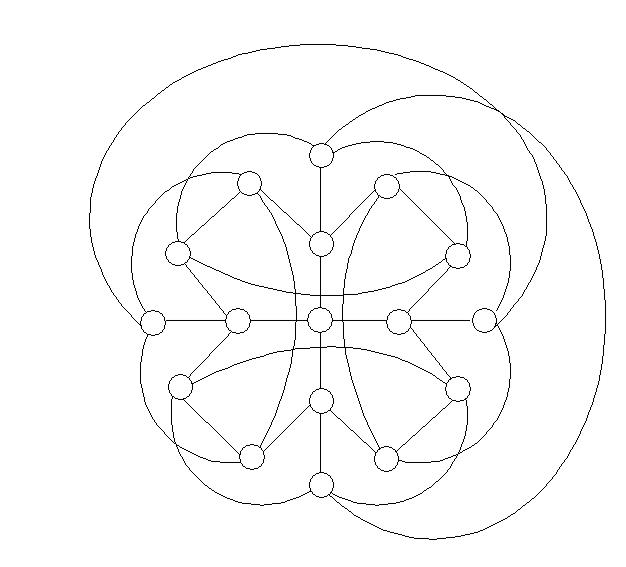
Рис. 18. Граф однородный степени 4 диаметра 3 с 17 вершинами.
Заметим, что не существует графа однородного степени 4 с 17 вершинами диаметра 2 (известная хорошая переборная задача для продвинутых старших школьников).
Несложно показать, что количество вершин у графа однородного степени k диаметра d не более 1+k*((k-1)d –1)/(k-2).
Граф называется сильно симметричным, если на нем группа автоморфизмов действует транзитивно. Это означает, что для любых двух вершин графа существует такой автоморфизм, который отображает первую вершину во вторую.
Примером однородного сильно симметричного графа малого диаметра является граф Петерсена. Граф Петерсена и трехмерный куб оба сильно симметричны и имеют одинаковую степень однородности, но при этом у графа Петерсена вершин больше, а диаметр меньше.
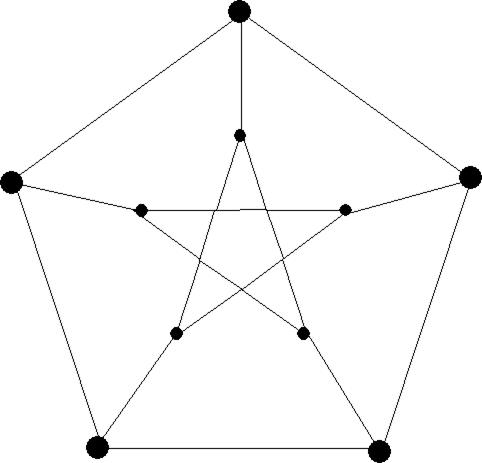
Рис. 19. Симметричный однородный степени 3 граф Петерсена с 10 вершинами и диаметром 2.
Дата: 2018-12-21, просмотров: 948.