Будем рассматривать задачу размещения данных с минимизацией межпроцессорных пересылок в суперкомпьютерах с распределенной памятью.
Будем предполагать, что имеется p процессоров, каждый из которых обладает своей локальной памятью, причем доступ к данным своей локальной памяти требует значительно меньших затрат времени, чем доступ к данным из локальной памяти другого процессора. Размещения данных будем рассматривать только линейные по модулю p, т.е. элемент массива X(i1,i2,...,im) находится в памяти процессора с номером u = (s1*i1+s2*i2+...+sm*im+s0) mod p, где s0,s1,s2,...sm – константы, зависящие только от массива X. К таким размещениям, в частности, относятся размещение матрицы по строкам или по столбцам или по диагоналям или скошенная форма хранения матрицы.
Далее будем рассматривать гнездо циклов, содержащее два вхождения массивов.
DO 1 I1 = 0, N1
................................... (16)
DO 99 In = 0, Nn
99… = X(a10+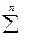 
a1j*Ij,..,am0+ 
amj*Ij) + Y(b10+ b1j*Ij,..,bk0+ bkj*Ij)
Будем рассматривать вопрос о том, когда эти вхождения оказываются в одном и том же модуле памяти.
Теорема 18. Пусть в гнезде циклов (16) есть два вхождения
X(a11*i1+...+a1n*in+a10, a21*i1+...+a2n*in+a20,..., am1*i1+...+amn*in+am0)
и
Y(b11*i1+...+b1n*in+b10, b21*i1+...+b2n*in+b20,..., bk1*i1+...+bkn*in+bk0)
m-мерного массива X и k-мерного массива Y соответственно.
Для того чтобы эти два вхождения были в одном и том же модуле памяти для всех значений счетчиков циклов i1,i2,...,in, необходимо и достаточно, чтобы выполнялись следующие условия
s1*a11+s2*a21+...+sm*am1 = t1*b11+t2*b21+...+tk*bk1 mod p
.........................................................................................
s1*a1n+s2*a2n+...+sm*amn = t1*b1n+t2*b2n+...+tk*bkn mod p
s1*a10+s2*a20+...+sm*am0+s0 = t1*b10+t2*b20+...+tk*bk0+t0 mod p
Доказательство. Поскольку оба вхождения из условия теоремы находятся в одном и том же модуле памяти должно выполняться равенство
s1*(a11*i1+...+a1n*in+a10)+s2*(a21*i1+...+a2n*in+a20)+...+ sm*(am1*i1+...+amn*in+am0)+s0 =
t1*(b11*i1+...+b1n*in+b10)+t2*(b21*i1+...+b2n*in+b20)+...+ tk*(bk1*i1+...+bkn*in+bk0) +t0 mod p
Так как это равенство должно тождественно выполняться для всех значений счетчиков циклов i1,i2,...,in, коэффициенты при этих счетчиках должны быть равны. Отсюда и вытекает заключение теоремы.
Конец доказательства.
Аналогичным образом доказывается следующая
Теорема 19. Пусть в гнезде циклов (16) есть два вхождения m-мерного массива X:
X(a11*i1+...+a1n*in+a10, a21*i1+...+a2n*in+a20,..., am1*i1+...+amn*in+am0) (17)
и
X(b11*i1+...+b1n*in+b10, b21*i1+...+b2n*in+b20,..., bm1*i1+...+bmn*in+bm0). (18)
Для того чтобы эти два вхождения были в одном и том же модуле памяти для всех значений счетчиков циклов i1,i2,...,in, необходимо и достаточно, чтобы выполнялись следующие условия
s1*(a11-b11)+s2*(a21-b21)+...+sm*(am1-bm1) = 0 mod p
......................................................................................... (19)
s1*(a1n-b1n)+s2*(a2n-b2n)+...+sm*(amn-bmn) = 0 mod p
s1*(a10-b10)+s2*(a20-b10)+...+sm*(am0-bm0) = 0 mod p
Для того чтобы оба вхождения (17) и (18) оказались в одном и том же модуле памяти при некотором наборе счетчиков циклов, должно выполняться условие:
(s1*(a11-b11)+s2*(a21-b21)+...+sm*(am1-bm1) )*i1 +(s1*(a1n-b1n)+s2*(a2n-b2n)+...
+sm*(amn-bmn))*i2 + (s1*(a10-b10)+s2*(a20-b10)+...+sm*(am0-bm0))*in =
= 0 mod p (20)
Общий вид решения этого уравнения следующий:
I1 = d11*t1+...+d1(n-1)*t(n-1)
I2 = d21*t1+...+d2(n-1)*t(n-1) (21)
………….
In = dn1*t1+...+dn(n-1)*t(n-1)
Где переменные (параметры) t1 , t2 , …, t(n-1) пробегают множество целых чисел Z.
Если не все коэффициенты уравнения (20) нули (что соответствует случаю (19) ), то решения уравнения (20) лежат в пространстве Zn на гиперплоскостях коразмерности 1, параллельных (21) и отстоящих друг от друга на расстоянии p. Статистически количество решений, при которых оба вхождения (17) и (18) оказываются в разных ПЭ, в (p-1) раз больше, чем решений, при которых эти вхождения оказываются в одном и том же ПЭ. Следовательно, требуется сделать пересылок nn-1 * (p-1) или один раз разослать все элементы массива во все процессоры: nm пересылок.
Примеры матричных алгоритмов с анализом размещения данных.
Пример 12.
do i = 1, n
do j = 1, n
B(i,j) = [A(i,j)+A(j,i)]/2
Для каждого значения i и каждого значения j элементы B(i,j), A(i,j) и A(j,i) должны оказаться в одном и том же модуле памяти. Это возможно тогда и только тогда, когда существуют такие целые числа s1, s2, t1, t2, что выполняются равенства
s1*i+s2*j = s1*j+s2*i = t1*i+t2*j mod p
Это возможно лишь при s1=s2=t1=t2 mod p. Например, все эти коэффициенты равны 1. Тогда в k-ом модуле памяти будет находиться k-ая косая диагональ (перпендикуляр к диагоналям) матрицы A и k-ая косая диагональ B – то есть множества элементов A(i,j) и B(i,j), для которых i+j = k (mod p) .
Пример 13. Рассмотрим фрагмент программы, вычисляющий произведение двух матриц.
do i = 1, n
do j = 1, n
do k = 1, n
X(i,j) = X(i,j)+A(i,k)*B(k,j).
Для каждого значения i, каждого значения j и каждого значения k элементы X(i,j), A(i,k) и B(k,j) должны оказаться в одном и том же модуле памяти. Это возможно тогда и только тогда, когда существуют такие целые числа s1, s2, t1, t2, u1, u2, что выполняются равенства
s1*i+s2*j = t1*i+t2*k = u1*k+u2*j mod p
Это возможно для всех значений i, j, k лишь при выполнении равенств s1=s2=t1=t2=u1=u2=0 mod p, т.е. когда все данные находятся в одном и том же модуле памяти. Итак, задача вычисления произведения матриц не может быть распараллелена на суперкомпьютере с MIMD архитектурой без межпроцессорных пересылок данных.
Пример 14.
do i = 1, n
do j = 1, n
B(i,j) = [A(i,j)+A(i-j,j)]/2
Размещение без пересылок возможно тогда и только тогда, когда существуют такие целые числа s1, s2, что выполняется равенство
s1*i+s2*j = s1*(i-j)+s2*j mod p
Это возможно лишь при s1=0 mod p (а S2 = 1).
Пример 15.
do i = 1, n
do j = 1, n
B(i,j) = [A(i,j)+A(i-j,i)]/2
Размещение массива A без пересылок невозможно. Действительно, если такое размещение существует, то существуют такие целые числа s1, s2, что выполняется равенство
s1*i+s2*j = s1*(i-j)+s2*i mod p
Это возможно лишь при s1=s2=0 mod p .
Пример 16.
do i = 1, N
do j = 1, N
B(i,j) = [A(i,j)+A(N-j,N-i)]/2
Размещение без пересылок возможно тогда и только тогда, когда существуют такие целые числа s1, s2, что выполняется равенство
s1*i+s2*j = s1*(N-j)+s2*(N-i) mod p
Если N кратно p, то это возможно при s1+s2=0 mod p .
Пример 17.
do i = 1, n
do j = 1, n
B(i,j) = [A(i,j)+A(n-j,i)]/2
Размещение массива A без пересылок невозможно. Действительно, если такое размещение существует, то существуют такие целые числа s1, s2, что выполняется равенство
s1*i+s2*j = s1*(n-j)+s2*i mod p
Это возможно для любых i, j лишь при s1=s2=0 mod p .
Пример 18. Распараллеливание алгоритма Флойда.
Алгоритм Флойда имеет на входе матрицу A весов дуг графа и преобразует ее в матрицу кратчайших расстояний.
do k = 1, n
do i = 1, n
do j = 1, n
if A(i,j) > A(i,k)+A(k,j) then
A(i,j) = A(i,k)+A(k,j)
Условие выполнения этого гнезда циклов без межпроцессорных пересылок на параллельном суперкомпьютере с распределенной памятью запишется в виде следующих равенств
s1*i+s2*j = s1*i+s2*k= s1*k+s2*j
Эти равенства могут выполняться тождественно для всех i, j, k только при s1=s2=0, т.е. при последовательном вычислении.
Операцию рассылки переменной во все процессоры будем обозначать broadcast, и использовать в следующем виде:
for i broadcast xi = y
Эта запись означает, что в каждом модуле памяти с номером i есть переменная xi и всем этим переменным (одновременно) присваивается значение переменной y.
Теорема 20. Пусть в суперкомпьютере с распределенной памятью есть операция broadcast и пусть n=p. Тогда алгоритм Флойда может быть выполнен за n2 пересылочных операций broadcast.
Для доказательства следует разместить элементы матрицы весов A так, что элемент A(i,j) находится в модуле памяти i mod p, после чего алгоритм может быть записан в виде
do k = 1, n
do j = 1, n
for i broadcast B(i,j) = A(k,j)
do par i = 1, n
if A(i,j) > A(i,k)+B(i,j) then
A(i,j) = A(i,k)+B(i,j)
Дата: 2018-12-21, просмотров: 505.
