Будем рассматривать цикл, в котором вычисляется переменная X:
DO I = 1, N (13)
X = GI(X);
Здесь Gi, i=1,...,N, – отображения из N-рекуррентного множества D. В частности, если GI(X)=X+A(I), то цикл (13) вычисляет сумму N чисел A(I), I=1,...,N.
Параллельное выполнение цикла (13) отличается от цикла (12) тем, что в межпроцессорных пересылках участвует меньшее количество данных. Для вычисления цикла (13) воспользуемся следующим алгоритмом:
1. В каждом ПЭ с номером k вычисляем ]N/p[ следующих суперпозиций Hk = Gk*]N/p[ о...оG(k-1)*]N/p[+1 . Это потребует (]N/p[-1)*Ta времени.
2. Пользуясь принципом сдваивания, вычисляем суперпозицию
W = Hp о...оH2 оH1
Это потребует log2(p) шагов, на каждом из которых вычисляется одна операция суперпозиция и выполняется одна межпроцессорная пересылка отображения Hk . Для универсальных коммутаторов или для гиперкуба здесь понадобится log2(p)*(Ta+T0), а для решетки – log2(p)*(Ta+T1)+T2*m* (p-1) времени (в частности, для кольцевой коммутационной сети – log2(p)*(Ta+T1)+T2*(p-1) времени).
3. За 1 шаг вычисляем W(X). Это отнимет Tb времени.
4. Конец.
Итак, для МВС с универсальным коммутатором или с архитектурой гиперкуба время работы оценивается величиной
F(p) = (]N/p[ - 1)*Ta+log2(p)*(Ta+T0)+Tb
и оптимальное количество ПЭ равно
p = N/(ln2*(1+T0/Ta)),
а для МВС с архитектурой m-мерной решетки –
F(p) = (]N/p[ - 1)*Ta+log (p)*(Ta+T1)+m* (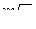 
- 1)*T2+Tb
и оптимальное количество ПЭ p удовлетворяет уравнению
p1+1/m * T2 + p * (Ta+T1)/ln(2) - N*Ta = 0 .
в частности, для МВС с кольцевой сетью –
F(p) = (]N/p[ - 1)*Ta+log (p)*(Ta+T1)+(p-1)*T2+Tb
и оптимальное количество ПЭ равно
p=(-(Ta+T1)+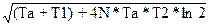 
)/(2*T2*ln2) ~ 
Остальные циклы и программы
Отметим, что, если цикл не содержит рекуррентностей, то независимо от вида коммуникационного устройства для его вычисления требуется времени
F(p) = ]N/p[ * Tb
При этом тело цикла может не принадлежать какому-либо N-рекуррентному множеству D.
Если же цикл имеет рекуррентную зависимость, но тело цикла не принадлежит какому-либо N-рекуррентному множеству D, то этот цикл надо вычислять последовательно, потратив времени F(p)=N*Tb+p*T0 для МВС с универсальным коммутатором и F(p)=N*Tb+p*T1 – для МВС с кольцевой сетью.
Предположим, что некоторая программа имеет вид последовательности циклов
DO I = 1, N1
ТЕЛОЦИКЛА1
DO I = 1, N2
ТЕЛОЦИКЛА2
....................
DO I = 1, Nm
ТЕЛОЦИКЛАm
Тогда время работы этой программы имеет следующий характер зависимости от p.
F(p) = a/p+b*log2p +c*p+d (14)
Вычислим производную от функции F и, приравняв ее к нулю, получим
c*p +b*p-a=0
Если a=0, то в тексте программы вообще нет циклов.
Если c=0, b=0 и a не равно 0, то производная от F отрицательна для всех p и, следовательно, чем больше количество используемых процессоров, тем быстрее выполнение программы. Это возможно при отсутствии каких-либо рекуррентных циклов.
Если c=0 и b не равно 0, то оптимальное количество ПЭ p=a/b. Эта ситуация возможна, если тело всякого рекуррентного цикла из текста программы принадлежит некоторому N-рекуррентному множеству D и в МВС используется коммутатор с кольцевой сетью. Отметим, что данное теоретически оптимальное значение p может превосходить максимально разумное значение.
Если c не равно 0, то оптимальное количество используемых ПЭ равно
p=(-b+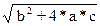 
)/(2*c).
Константы a,b,c,d, входящие в формулу функции F, можно найти методом неопределенных коэффициентов, вычислив исследуемую программу для четырех различных значений p.
Случай программы с кратными циклами сводится к предыдущему.
Действительно, двойной цикл
DO J=1, M
DO I=1, N
ТЕЛОЦИКЛА(I,J)
можно рассматривать, как M циклов по I.
Зависимость времени работы программы от количества ПЭ имеет такой же вид (14) и при более сложных гнездах циклов, у которых границы изменения параметров внутренних циклов являются функциями от параметров объемлющих циклов. Однако формула (14) может быть нарушена, например, условными операторами в тексте программы.
Дата: 2018-12-21, просмотров: 478.
