Треугольная (полнодоступная) коммутационная схема для 8 входов содержит 6 коммутационных элементов.

Рассмотрим неразделенную коммутационную схему, изоморфную в теоретико-графовом смысле трехкаскадной разделенной коммутационной схеме. Нетрудно убедиться, что такая схема для 8 входов тоже является полнодоступной.

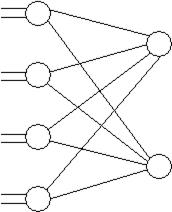
       Рис. 43. Полнодоступный неразделенный коммутатор с 8 входами и 6 четырехвходовыми элементами.

       Но для большего количества входов построенная по такому принципу схема уже не полнодоступна. Представленная на следующем рисунке схема не может реализовать разбиение входов на пары: (1,3), (2,5), (4,6), (7,9), (8,10)…

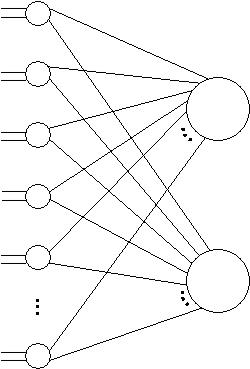
       Рис. 44. Трехкаскадная коммутационная неразделенная схема с четырехвходовыми элементами и с количеством входов более 8 не полнодоступная.

       Приведем один из возможных подходов построения логарифмической (приближающейся к нижней оценке) неразделенной коммутационной схемы. Такую схему будем собирать из восьмивходовых элементов, как изображено на следующем рисунке.

       Рис. 45. Полнодоступная трехкаскадная коммутационная неразделенная схема с восьмивходовыми элементами.

Теорема 14. Представленная выше трехкаскадная неразделенная коммутационная схема с n входами является полнодоступной.

       Доказательство. Пусть задано произвольное разбиение входов на пары, описанное подстановкой s длины n (квадрат которой равен тождественной). Опишем алгоритм, который по произвольной подстановке s определяет состояние коммутатора, реализующее соединение всех пар, соответствующих подстановке входов.

       Построим вспомогательный неориентированный граф. Вершинами этого графа являются элементы внешнего каскада (первого и третьего каскадов). Для каждого i = 1, 2, …, n определяется ребро графа (x_]i/4[ , y_]t/4[), где t = s_i . Каждое ребро вспомогательного графа соответствует соединению одной пары входов. Несложно проверить, что полученный граф является однородным степени 4. В частности, все компоненты связности этого графа являются эйлеровыми графами. Найдем в каждой компоненте связности вспомогательного графа эйлеров цикл (цикл, содержащий каждое ребро в точности один раз). Поскольку степень каждой вершины равна 4, несложно доказать, что количество ребер в каждом таком цикле – четное. Следовательно, в каждом таком эйлеровом цикле ребра можно, чередуясь, пометить символами A₁ и A₂ . Эти символы показывают, через какой элемент центрального каскада проходит путь, соединяющий входы, соответствующие рассматриваемому ребру.

Описанное определение путей, реализующих соединения, корректно. Действительно, в эйлеровом цикле каждое ребро встречается ровно 1 раз. Поскольку степень каждой вершины равна 4, каждая вершина в этом цикле встретится дважды. Инцидентные вершине ребра в цикле находятся рядом с вершиной: одно слева и одно справа. Следовательно, при каждом вхождении вершины графа в эйлеров цикл одно из этих ребер будет помечено символом A₁ , а другое – A₂ . В итоге из четырех ребер, инцидентных вершине, два будут помечены символом A₁ , а другие два – символом A₂ .

Конец доказательства.

Теорема 15. Пусть число n имеет вид n = 8*2^k . Существует полнодоступная коммутационная неразделенная схема с n входами, состоящая только из восьмивходовых элементов, количество которых равно (n/4)*log₂n – 5*n/8 .

       Доказательство. Такая схема описана выше. Подсчитаем количество элементов в этой схеме. Обозначим через F(n) количество восьмивходовых неразделенных элементов в рассматриваемой схеме. Тогда, учитывая, что F(8) = 1, получим

 F(n) = n/4 + 2*F(n/2) = n/4 + 2*{n/8 + 2*F(n/4)} = … =

= (n/4)*k + 2^k = (n/4)*(log₂n – 3) + 2^(log₂n – 3) = (n/4)*log₂n – 5*n/8 .

       Конец доказательства.

Следствие. Пусть число n имеет вид n = 8*2^k . Существует полнодоступная коммутационная неразделенная схема с n входами, состоящая только из четырехвходовых элементов, количество которых равно 6*{(n/4)*log₂n – 5*n/8} .

Другой неразделенный коммутатор с количеством элементов O(n*log₂n) приводится в [1]. Еще следует отметить неразделенный коммутатор с петлевыми соединениями, который конструируется из разделенного коммутатора и еще двух каскадов коммутационных элементов [6].