Иногда возникает задача переноса программ с одних многопроцессорных вычислительных систем на другие. При этом вычислительные системы могут отличаться не только количеством вычислительных устройств, но и коммуникационной системой. Тогда возникает проблема выполнения пересылок, ориентированных на одну сеть, на другой сети. Это приводит к задачам моделирования пересылок одной сети на другой. В работе [37, стр. 64] рассмотрено моделирование на гиперкубе кольцевой сети с помощью кодов Грея. В [37, стр. 66] рассмотрено моделирование на гиперкубе двумерной решетки, у которой на сторонах количества узлов являются степенью двойки.
Если сеть имеет гамильтонов цикл (цикл, проходящий через каждую вершину в точности один раз), то такой цикл и можно взять в качестве кольцевой сети. Покажем, как построить гамильтонов цикл на прямоугольной решетке типа тор. Допустим, что у прямоугольной решетки одна хотя бы из сторон содержит четное количество узлов. Пусть размерность этой решетки m*(2*k) . Тогда номера узлов, изображенные на следующем рисунке, показывают гамильтонов цикл на этой решетке
| 1 | 2*m | (2*m+1) | m*(2*k) | ||
| 2 | 2*m-1 | (2*m+2) | m*(2*k)-1 | ||
| … | |||||
| (m-1) | (m+2) | ||||
| m | (m+1) | 3*m | 3*m+1 | … | m*(2*k-1) |
Рис. 20. Выделение кольцевого соединения на двумерном торе с четным количеством узлов.
Пусть теперь прямоугольная решетка содержит нечетное количество узлов (2*m+1)*(2*k+1) . В этом случае в решетке выделяется подрешетка размерности (2*m)*(2*k), узлы которой нумеруются указанной выше последовательности. Тогда нумерация узлов исходной решетки будет выглядеть следующим образом.
| 1 | 2*m | (2*m+1) | m*(2*k) | m*(2*k)+1 | ||
| 2 | 2*m-1 | (2*m+2) | m*(2*k)-1 | m*(2*k)+2 | ||
| … | ||||||
| (m-1) | (m+2) | |||||
| M | (m+1) | 3*m | 3*m+1 | … | m*(2*k-1) | m*(2*k+1) |
| (m+1)*(2*k+1) | m*(2*k+1)+2 | m*(2*k+1)+1 |
Рис. 21. Выделение кольцевого соединения на двумерном торе с нечетным количеством узлов.
У многокольцевых соединений, как правило, одно из колец является гамильтоновым циклом.
Рассмотрим задачу эмуляции n-мерный куба на кольце с количеством узлов p=2n.
Напомним, что вершины n-мерного куба кодируются булевыми векторами
(x1, x2, …, xn) длины n.
К сожалению, коды Грея [37, стр. 64] для этой задачи не удобны. Действительно, для n=3 расстояние по кольцу между вершинами, соответствующими (0,0,0) и (1,0,0) равно 1, а расстояние между (0,0,1) и (1,0,1) равно 4. Хотя оба этих ребра n-куба соответствуют изменению первой координаты. Во многих задачах пересылки данных по таким ребрам предполагается выполнять одновременно. В данном примере на кольце эти пересылки будут выполняться разное время.
Для случая n = 2 задача тривиальная, поскольку 2-мерный куб представляет собой кольцо с 4 вершинами. Вершинам 2-мерного куба (0,0), (0,1), (1,1) (1,0) сопоставляются узлы кольцевой сети с номерами 0, 1, 2, 3 соответственно. Обозначим это сопоставление j: j(0,0) = 0, j(0,1) = 1, j(1,1) =2, j(1,0) =3.
Определим сопоставление вершин n-мерного куба узлам кольцевой сети для n>2 по следующей формуле
j(x1, x2, …, xn) = (x1+2*x2+…+2n-3 * xn-2) + 2n-2 * j(xn-1, xn)
Первое слагаемое в данной формуле – это число, состоящее из первых n-2 цифр двоичного кода вершины n-мерного куба.
Рассмотрим подробнее указанное сопоставление узлов n-мерного куба узлам кольца. Сопоставление узлов n-мерного куба узлам кольца будем строить по индукции.
Предположим, что построено сопоставление узлов n-мерного куба узлам кольца для n=k, k>1. Построим такое сопоставление для n=k+1.
Пусть узлы кольца занумерованы от 0 до (n-1). Рассмотрим подмножество узлов кольца с четными номерами. Это подмножество можно рассматривать, как кольцевую сеть, в которой пересылка между соседними узлами в 2 раза дольше, чем в исходной кольцевой сети. Это подкольцо будем называть 0-подкольцо. Аналогично, узлы с нечетными номерами образуют подкольцо, которое будем называть 1-подкольцом.
Пусть (x1, x2, …, xk+1) – произвольная вершина (k+1)-мерного куба. Рассмотрим подмножество вершин n-мерного куба, состоящее из векторов (0, x2, …, xk+1). Это подмножество порождает подграф, изоморфный k-мерному кубу. Узлы этого k-мерного куба сопоставим узлам 0-подкольца. Аналогично, подмножество вершин (1, x2, …, xk+1) также порождает подграф, изоморфный k-мерному кубу. Узлы этого k-мерного куба сопоставим узлам 1-подкольца.
Рассмотрим в n-мерном кубе множество ребер, соединяющих вершины вида (x1, …, xi-1, 0, xi+1,…, xk+1) и (x1, …, xi-1, 1, xi+1,…, xk+1). Ребра n-мерного куба, принадлежащие одному такому множеству, будем называть однотипными. Всего получается n типов ребер. При реализации принципа сдваивания на n-мерном кубе используются одновременные пересылки по однотипным ребрам. Поэтому, при моделировании n-мерного куба на кольце важно, чтобы такие пересылки эффективно реализовывались.
Теорема 9. При описанном выше сопоставлении вершинам n-мерного куба узлов кольцевой сети расстояние между концевыми узлами всех однотипных ребер одинаково.
Следствие. Пересылки на кольце, соответствующие пересылкам по однотипным ребрам n-мерного куба требуют одинаковое время.
3.2 Вопросы и задания.
- Правда ли, что трехмерный куб среди графов однородных степени 3 и с диаметром 3 имеет наибольшее количество вершин?
- Чему равен диаметр четырехмерного куба?
- Какой длины маршрут (путь) на шестимерном кубе между вершинами A=(0,1,1,0,0,1) и B=(1,1,0,1,0,0) ?
- Существует ли граф однородный степени 3 диаметра 2 с 10 вершинами?
- Существует ли граф однородный степени 5 диаметра 2 с 19 вершинами?
- Существует ли граф однородный степени 4 диаметра 2 с 17 вершинами?
- Какой диаметр у бинарного дерева с N вершинами?
- Какой длины стороны у прямоугольной двумерной решетки наименьшего диаметра, соединяющей 1800=2*2*2*3*3*5*5 узлов? 40*45 (лучше, чем 30*60)
Коммутаторы.
Сначала коммутаторы использовались для телефонной связи группы абонентов. В некоторых старых фильмах встречаются эпизоды о том, как абонент звонит на телефонную станцию и просит «барышню» соединить его с «другим героем фильма». «Барышня» втыкала шнур звонящего абонента в гнездо абонента, которому адресован, – и абоненты могли разговаривать. После таких «ручных» коммутаторов появились автоматические коммутаторы, построенные на контактно-релейных схемах. Сейчас, разумеется, используются электронные схемы.
Для организации обмена данными между устройствами также используются электронные коммутаторы. Принципы построения коммутаторов для параллельных вычислительных систем такие же, как и для систем телефонной связи.
Коммутатор – это устройство, имеющее входы и выходы и позволяющее соединять некоторые комбинации этих входов и выходов.
Если входы и выходы у коммутатора отличаются, то такой коммутатор называется разделенным. Если входы и выходы коммутатора не отличаются, то будем говорить только о входах коммутатора, а сам коммутатор будем называть неразделенным.

Рис. 22. Входы (слева) и выходы (справа) разделенного коммутатора.
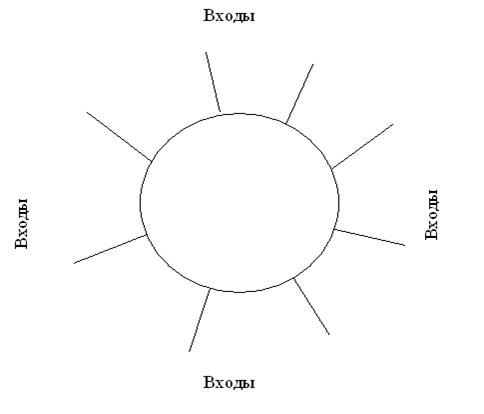
Рис. 23. Входы неразделенного коммутатора.
Задача синтеза коммутатора состоит в том, чтобы из коммутаторов малой размерности собрать большой коммутатор с заданными свойствами. Будем рассматривать такие важные свойства коммутатора, как (определяемые далее) полнодоступность и неблокируемость. Для полнодоступных коммутаторов приводятся нижние оценки количества коммутационных элементов (малых коммутаторов), из которых собирается рассматриваемый коммутатор.
Более подробно с коммутационными схемами можно познакомиться в [6], [15], [57].
Разделенные коммутаторы.
Элементарные коммутаторы и коммутационные схемы.
Элементарный разделенный двоичный коммутатор имеет два входа и два выхода. Такой коммутатор может быть в двух состояниях:
1. первый вход соединяется с первым выходом, а второй вход – со вторым;
2. первый вход соединяется со вторым выходом, а второй вход – с первым.
Первое состояние можно условно называть «равенство», а второе состояние – «крестик».
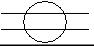
Рис. 24. Элементарный разделенный двоичный коммутатор в состоянии «равенство».
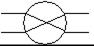
Рис. 25. Элементарный разделенный двоичный коммутатор в состоянии «крестик».
Соединяя выходы одних элементарных коммутаторов с входами других, можно получать коммутационные схемы, которые для простоты будем также называть коммутаторами. Состояние коммутационной схемы – это множество состояний ее элементов (элементарных коммутаторов).
В качестве элементарных коммутаторов не обязательно рассматривать двоичные – могут рассматриваться и элементарные коммутаторы большей размерности.
Элементарные коммутаторы будем еще называть коммутационными элементами.
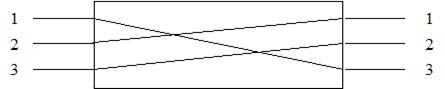
Рис. 26. Одно из состояний элементарного разделенного коммутатора с тремя входами и тремя выходами.
Задание на коммутацию.
Пусть у коммутатора есть n входов и m выходов. Будем рассматривать коммутаторы, у которых один вход может быть соединен только с не более чем одним выходом. Пусть входы и выходы пронумерованы от 1 до n или m соответственно. Если какой-нибудь выход не следует соединять ни с одним входом или вход не следует соединять ни с одним выходом, то будем считать, что таким выходу и входу соответствует вход или выход с номером 0. Тогда задание на коммутацию может быть описано отображением множества {0,1,…,n} в {0,1,…,m} или {0,1,…,m} в {0,1,…,n}. При этом 0 в обоих случаях отображается в 0.
Пример 3. В следующей таблице описано задание на соединение коммутатора, у которого 6 выходов и не менее 5 входов.
| Выходы | 1 | 2 | 3 | 4 | 5 | 6 |
| Входы | 0 | 5 | 2 | 1 | 0 | 4 |
В том случае, когда количество входов равно количеству выходов и все входы и выходы задействованы, отображение, задающее коммутацию, является биективным, и задание на коммутацию может быть записано подстановкой.
|
s= | 1 | 2 | … | n |
| s1 | s2 | sn |
Здесь в первой строке записаны номера выходов, а во второй строке – номера входов коммутатора.
Подстановку можно рассматривать не только как отображение множества выходов на множества входов, но и, наоборот, как отображение множества входов на множество выходов. Поскольку нам привычнее сначала рассматривать входы, а затем выходы, то в случае подстановок естественнее верхнюю строчку считать номерами входов, а нижнюю – номерами выходов.
Далее, в основном, если особо не оговорено, будем рассматривать только такие коммутаторы, которые в один момент времени позволяют соединять один вход лишь с одним выходом (в этот же момент другие входы могут быть соединены с другими выходами) и в которых количество входов равно количеству выходов. Ввиду такого ограничения задание на соединение входов и выходов коммутатора на какой-либо момент времени имеет вид подстановки:
S = 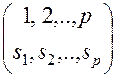
В верхней строке подстановки стоят номера входов коммутатора, а в нижней строке – номера выходов, с которыми должны соединяться соответствующие входы.
Полнодоступность.
Разделенный коммутатор с n входами и n выходами будем называть слабо полнодоступным, если любой вход может быть соединен с любым выходом.
Разделенный коммутатор с n входами и n выходами будем называть полнодоступным, если для любой подстановки s существует такая настройка коммутатора, при которой для любого i = 1, 2, …, n выход с номером i соединяется с входом с номером si.
Рассматриваемые в данной главе элементарные коммутаторы предполагаются полнодоступными.
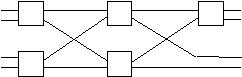
Рис. 27. Полнодоступный разделенный коммутатор с четырьмя входами и четырьмя выходами, состоящий из пяти двоичных элементов.
Оценка снизу для количества элементов полнодоступного разделенного коммутатора.
Пусть полнодоступная разделенная коммутационная схема с n входами и n выходами состоит из N двоичных коммутационных элементов. Тогда количество заданий на коммутацию равно количеству подстановок из n чисел и равно n! С другой стороны, количество состояний коммутационной схемы из N двоичных элементов равно 2N . Если схема полнодоступна, то каждое задание на коммутацию должно быть реализовано хотя бы одним состоянием. Следовательно, для полнодоступной схемы должно выполняться неравенство
n! ≤ 2N
Из этого неравенства с использованием формулы Стирлинга вытекает нижняя оценка количества двоичных элементов полнодоступной разделенной коммутационной схемы.
N ≥ log2(n!) ≈ log2(nn/en * (2*π*n)1/2 ) = n*log2(n) – n*log2(e) + (1/2) * log2(2*π*n) ≈ n*log2(n) – n*log2(e)
Аналогично может быть получена нижняя оценка количества k*k – элементов в полнодоступной разделенной коммутационной схеме.
N ≥ logk!(n!) ≈ log k!(nn/en * (2*π*n)1/2 ) = 1/ log2(k!) * (n*log2(n) – n*log2(e) + (1/2) * log2(2*π*n) )≈ 1/ log2(k!) * (n*log2(n) – n*log2(e))
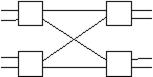
Рис. 28. Коммутационная схема, состоящая из 4 двоичных элементов, не является полнодоступной, поскольку имеет количество состояний 24 = 16 , меньшее, чем количество заданий на коммутацию 4!=24.
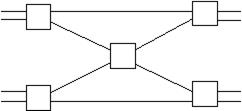
Рис. 29. Коммутационная схема, состоящая из 5 двоичных элементов, не является полнодоступной, поскольку никакое состояние не реализует коммутацию, заданную следующей подстановкой
|
s= | 1 | 2 | 3 | 4 |
| 3 | 4 | 1 | 2 |
Матричный разделенный коммутатор.
Матричный разделенный коммутатор представляет собой прямоугольную матрицу элементарных двоичных коммутаторов, каждый из которых соединен с соседями сверху, снизу, слева и справа.
Квадратный матричный коммутатор является полнодоступным. Это показывает следующий алгоритм настройки матричного коммутатора. Для любой подстановки s длины n, для каждого номера i=1,2,…,n следует коммутационный элемент, стоящий в i-ой строке и столбце si , привести в состояние «равенство», а остальные элементы в строке – в состояние «крестик».
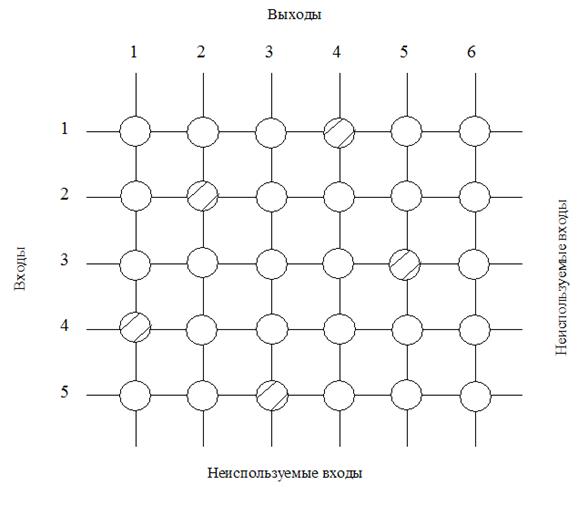
Рис. 30. Пример матричного коммутатора.
Матричный коммутатор обладает еще таким важным свойством, как неблокируемость. Это означает, что при желании изменить соединения некоторых входов и выходов остальные соединения можно не перенастраивать. Более экономичные неблокирующие схемы Клоза рассмотрены, например, в [15]. Далее будут рассматриваться полнодоступные коммутаторы, которые не обладают таким свойством.
Количество элементов матричного коммутатора с n входами и m выходами равно n*m. Квадратный коммутатор имеет n2 элементов.
Треугольный коммутатор.
Оказывается, что можно обойтись лишь половиной элементов матричного коммутатора, сохранив полнодоступность и пожертвовав неблокируемостью. Треугольный разделенный коммутатор с n входами и n выходами имеет следующий вид.
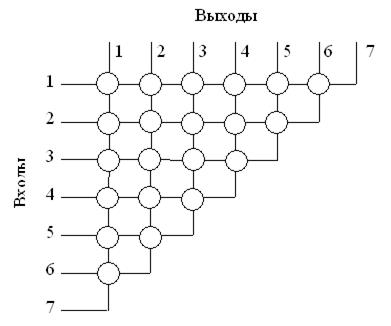
Рис. 31. Пример треугольного коммутатора.
Приведем алгоритм настройки треугольного коммутатора.
Пусть задана некоторая подстановка s длины n. Будем иллюстрировать алгоритм на примере подстановки
| Выходы | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Входы | 3 | 6 | 1 | 7 | 2 | 5 | 4 |
Настраивать будем строки треугольного коммутатора, начиная с первой. В первой строке все элементы от 1-ого до элемента с номером (s1 -1) приводим в состояние «крестик», а остальные – в состояние «равенство». Выбрасываем 1-ую строку элементов из коммутатора и получаем треугольный коммутатор размерности на 1 меньше. Номера входов оставляем прежние. Номера выходов переписываем от предыдущего шага, пропуская номер si .
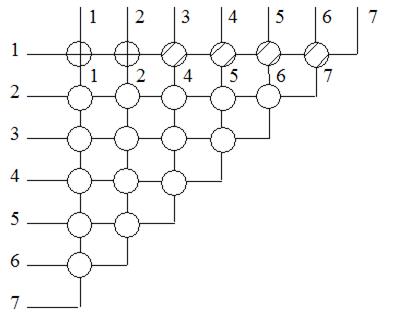
Рис. 32. Настройка первой строки треугольного коммутатора.
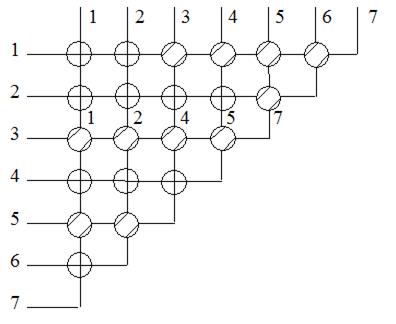
Рис. 33. Окончательная настройка треугольного коммутатора.
Количество элементов разделенного треугольного коммутатора с n входами и n выходами равно n*(n-1)/2 .
Логарифмический коммутатор.
В этом параграфе описывается разделенная коммутационная схема с n входами и n выходами, состоящая из коммутационных элементов k*k. В случае k=2 эта схема состоит из n*log2(n) двоичных коммутационных элементов. Таким образом, нижняя оценка количества необходимых двоичных коммутационных элементов оказывается практически достижимой. Обоснование полнодоступности этой схемы опирается на следствие известной комбинаторной теоремы Холла о свадьбах (о танцах).
Под каскадом понимается вертикальная линейка коммутационных элементов.
Пусть число n делится нацело на k. Рассмотрим трехкаскадную коммутационную разделенную схему с n входами и n выходами следующего вида.
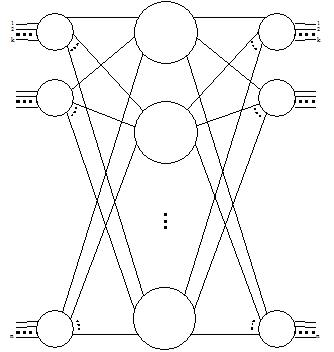
Рис. 34. Трехкаскадная разделенная коммутационная схема. Первый и третий каскады состоят из n/k элементарных коммутаторов k*k . Центральный каскад состоит из k полнодоступных разделенных коммутаторов с n/k входами и n/k выходами.
Теорема 10. Представленная выше трехкаскадная разделенная коммутационная схема с n входами и n выходами является полнодоступной.
Доказательство. Пусть s – произвольная подстановка длины n. Для каждого i = 1, 2, …, n существует k путей от входа с номером i к выходу si
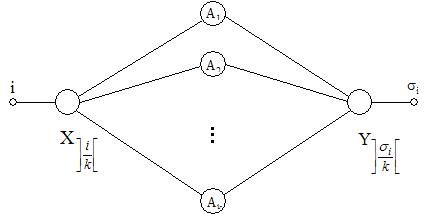
Рис. 35. Множество из k возможных путей от входа с номером i к выходу si.
Построим вспомогательный двудольный граф. Вершинами этого графа являются элементы первого и третьего каскадов. Для каждого i = 1, 2, …, n определяется дуга графа (x]i/k[, y]t/k[) , где t = si . Несложно проверить, что полученный граф является однородным степени k.
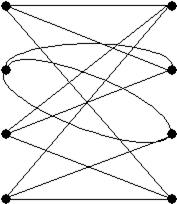
Рис. 36. Вспомогательный граф для случая n=12, k=3, n/k=4, s = (4,2,12,7,5,9,11,1,6,10,8,3).
Каждая дуга вспомогательного графа соответствует соединению одной пары вход-выход. Каждой дуге вспомогательного графа следует приписать имя одного из элементов среднего каскада коммутационной схемы: A1, A2,…, Ak. При этом разные дуги, инцидентные одной и той же вершине x]i/k[ (или y]t/k[ , где t = si ), должны быть помечены различными именами элементов среднего каскада. Это требование вытекает из того, что элемент x]i/k[ (или y]t/k[ , где t = si ) соединен с элементом Aj , j = 1, 2, …, k, только одной связью.
Таким образом, для определения путей между входами i и выходами si , i = 1, 2, …, n, следует все дуги вспомогательного графа пометить именами A1, A2,…, Ak так, чтобы из каждой вершины xs выходила ровно одна дуга каждого вида A1, A2,…, Ak и в каждую вершину yr входила ровно одна дуга каждого вида A1, A2,…, Ak .
Алгоритм раскраски дуг вспомогательного графа символами A1, A2,…, Ak выглядит следующим образом.
Найдем во вспомогательном графе совершенное паросочетание (поскольку вспомогательный граф однородный, из следствия теоремы Холла вытекает, что такое паросочетание существует). Все дуги найденного паросочетания пометим символом A1. Выбросим все дуги найденного паросочетания из вспомогательного графа. Оставшийся граф опять будет однородным (степени k-1). Следовательно, в нем существует совершенное паросочетание. Найдем его и все его дуги пометим символом A2 . Выбросим помеченные дуги и т.д.
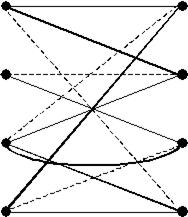
Рис. 37. Разбиение множества дуг вспомогательного графа на совершенные паросочетания.
Таким образом, для каждой пары «вход-выход» из задания на соединение определилось, через какой элемент центрального каскада это соединение реализуется, при этом все n соединений не конфликтуют между собой и могут существовать одновременно.
Конец доказательства.
Пусть число n является степенью числа k. Тогда в рассматриваемой трехкаскадной схеме каждый элемент центрального каскада может быть опять представлен в виде трехкаскадного коммутатора. А центральный каскад нового коммутатора опять можно представить в виде трехкаскадной схемы и т.д. В результате можно получить коммутатор, состоящий только из элементов k*k. Ясно, что этот коммутатор будет полнодоступным. В результате настройки исходного трехкаскадного коммутатора определяется задание для коммутаторов центрального каскада.
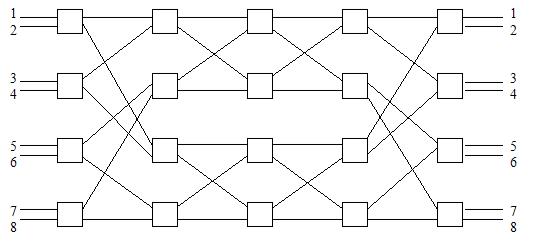
Рис. 38. Полнодоступный разделенный коммутатор с 8 входами и 8 выходами, состоящий из 20 элементов 2*2.
Теорема 11. Пусть число n является степенью числа k. Существует полнодоступная коммутационная разделенная схема с n входами и n выходами, состоящая только из элементов k*k, количество которых равно 2*(n/k)*logkn – n/k .
Доказательство. Такая схема описана выше. Подсчитаем количество элементов в этой схеме. Обозначим через F(n) количество элементов k*k в рассматриваемой схеме. Тогда, учитывая, что F(k) = 1, получим
F(n) = 2*(n/k) + k*F(n/k) = 2*(n/k) + k*{2*(n/k2) + k*F(n/k2)} = … =
= 2*(n/k)*(logkn – 1) + k^(logkn – 1) = 2*(n/k)*logkn – (n/k).
Конец доказательства.
Следствие. В частности, при k=2 и n, равном степени двойки, получаем полнодоступную разделенную коммутационную схему, состоящую из n*log2n – n/2 двоичных коммутационных элементов. Это количество совпадает с нижней оценкой в первом члене асимптотического разложения.
Из полученных оценок можно сделать вывод о больших технических затратах вплоть до невозможности использования полнодоступных коммутационных схем при большом количестве входов и выходов. Действительно, начиная с некоторого момента, затраты на коммутацию могут превысить затраты на совокупность всех процессоров.
Неразделенные коммутаторы.
Топология неразделенных коммутаторов во многом похожа на топологию разделенных коммутаторов. В данном параграфе будут рассмотрены треугольный и логарифмический неразделенные коммутаторы.
Задание на коммутацию.
Пусть имеется неразделенный коммутатор с n входами. Этот коммутатор должен реализовывать соединения между парами входов. Задание на соединение такого коммутатора может быть описано, как и в случае разделенного коммутатора, подстановкой. Но не всякая подстановка описывает задание на соединение входов неразделенного коммутатора. Подходящие подстановки, очевидно, должны обладать следующим свойством: если входу j соответствует вход k, то входу k должен соответствовать вход j. Такие подстановки представляются в виде произведения независимых транспозиций. Квадрат такой подстановки (суперпозиция такой подстановки с самой собой) равен тождественной подстановке. Среди подстановок, обладающих такими свойствами, есть и такие, в которых некоторому номеру k может соответствовать этот же номер.
Пример 4. Подстановка, квадрат которой равен тождественной, с неиспользуемыми входами.
|
s= | 1 | 2 | 3 | 4 |
| 3 | 2 | 1 | 4 |
Входы, которые в подстановке соответствуют самим себе, будем считать неиспользуемыми.
Дата: 2018-12-21, просмотров: 1135.