Пусть D – подмножество R^m и D – множество отображений пространства D в D, которое замкнуто относительно операции суперпозиции. Будем говорить, что множество D является рекуррентно замкнутым, если выполняются следующие требования:

1. Множество D замкнуто относительно операции суперпозиции.

2. Существует число Ta и алгоритм, который для любых двух отображений G₁ и G₂ из D вычисляет суперпозицию G₁ о G₂  за время Ta.

3. Существует число Tb и алгоритм, который для любого G из D и x из D вычисляет G(x) за время Tb.

4. Вычисление суперпозиции на компьютере является ассоциативной операцией на D. (Теоретически суперпозиция отображений всегда ассоциативна, но, как известно, это свойство может нарушаться из-за погрешности округлений на компьютере).

Будем говорить, что множество D является N-рекуррентно замкнутым, если выполняются условия 1-3, а вместо условия 4 выполняется следующее условие:

4а. Если вычисление суперпозиции N отображений из D на компьютере выполнить по-разному, т.е. изменив порядок взятия операций суперпозиции, то результаты будут отличаться на пренебрежимо малую величину.

Описанное абстрактное множество D было введено в [99] для исследования параллельного выполнения рекуррентных программных циклов с условными операторами.

Ясно, что множество D рекуррентно замкнуто тогда и только тогда, когда оно N-рекуррентно замкнуто для любого N. Далее будут рассматриваться циклы с N итерациями, тела которых представляют собой отображения из некоторого N-рекуррентно замкнутого множества D.

Пример 9. Пусть D = Z^m , тогда множество D всех линейных отображений из Z^m в Z^m вида y=Ax , где A – матрица с целыми коэффициентами, удовлетворяет указанным выше требованиям.

Пример 10. Пусть D = R^m , тогда, если погрешность округлений на компьютере достаточно мала, то множество D всех линейных отображений из R^m в R^m удовлетворяет указанным выше требованиям. Это возможно, если количество разрядов в машинном слове достаточно велико для рассматриваемых погрешностей и значений N.

Пример 11. Множество D всех булевых отображений вида

f(X) = PÙX Ú QÙØX Ú R удовлетворяет указанным выше требованиям.

Вычисление массивов данных

Будем рассматривать цикл, в котором вычисляются элементы массива:

DO I = 1, N                                                                                            (12)

X(I) = G_I(X(I-1));

Здесь G_I, I=1,...,N – отображения из N-рекуррентного множества D. В частности, если m=1, G_I(Y)=Y+A(I), то цикл (12) для каждого k=1,...,N вычисляет суммы чисел A(I), I=1,...,k. Для вычисления этого цикла воспользуемся следующим алгоритмом, предполагающим вертикальное размещение массивов:

1. В каждом ПЭ с номером k вычисляем ]N/p[ следующих суперпозиций H_ki = G_k*]N/p[-i+1 o...oG_{(k-1)*]N/p[+1} . Это потребует (]N/p[-1)*Ta времени. Здесь Ta – время вычисления G_I(X)

2. Пользуясь принципом сдваивания [25, с.34], вычисляем все суперпозиции

W₁ = H₁₁

W₂ = H₂₁ oH₁₁

......

W_k = H_k1 o...oH₂₁ oH₁₁

............

W_n = H_n1 o... oH₂₁ oH₁₁

Это потребует log₂p шагов, на каждом из которых вычисляется одна операция суперпозиции и выполняется одна межпроцессорная пересылка отображения H_k1 . Для универсальных коммутаторов и гиперкуба здесь понадобится log₂p*(Ta+T0) тактов, а для m-мерной решетки – log₂p*(Ta+T1)+T2*k*( 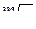 - 1) тактов (в частности, для кольцевой коммутационной сети – log₂p *(Ta+T1)+T2*(p-1) ).

3. Одновременно за 1 шаг в каждом ПЭ с номером k вычисляем W_k(X(0)). Это отнимет Tb времени.

4. Одновременно за ]N/p[ шагов в каждом ПЭ с номером k вычисляем значения G_i(W_k(X(0))) для всех индексов i, для которых G находится в этом ПЭ. Это требует ]N/p[*Tb времени.

5. Конец.

Итак, для МВС с универсальным коммутатором или с архитектурой гиперкуба время работы оценивается величиной

F(p) = (]N/p[ - 1)*Ta+log (p)*(Ta+T0)+(]N/p[+1)*Tb =

]N/p[ *(Ta+Tb)+log (p)*(Ta+T0)+(Tb-Ta),

оптимальное количество ПЭ равно

      p = N*(Ta+Tb)*ln2/(Ta+T0),

минимальное время работы равно

(Ta+T0)* 1/ln2+ln((Ta+Tb)*ln2/(Ta+T0)) +Tb-Ta.

Для МВС с m-мерной решеткой время работы оценивается величиной

F(p) = (]N/p[-1)*Ta+log (p)*(Ta+T1)+m*( 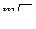 -1) * T2+(]N/p[+1) * Tb = ]N/p[ *(Ta+Tb)+log (p)*(Ta+T1)+m*(  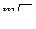- 1)*T2+(Tb-Ta),  

оптимальное количество ПЭ вычисляется из уравнения

p^1+1/m * T2 + p * (Ta+T1)/ln(2) - N*(Ta+Tb) = 0 .

Это уравнение подстановкой y = p^-1/m сводится к полиномиальному

y^m+1 *N*(Ta+Tb) - y * (Ta+T1)/ln(2) - T2 = 0 .

В частности, для МВС с кольцевой сетью время оценивается величиной

F(p) = ]N/p[ *(Ta+Tb)+log (p)*(Ta+T1)+(p-1)*T2+(Tb-Ta),

оптимальное количество ПЭ равно

p=(-(Ta+T1)+ /(2*T2*ln2) ~  

и минимальное время работы равно

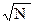 * ( (Ta+Tb)*  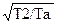+  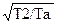)+ln(N)*(Ta+T1)/2+ (Ta+T1)/2*ln(Ta/T2)-T2+Tb-Ta.