Выглядит как довльно тяжелый пример для старта, но не паникуйте, он на самом деле довольно простой. Как обычно, будем двигаться постепенно:
✴ Посмотрите на величину тысяч (the numbers to the left of the
comma), 314 в данном примере
✴ Так как 314 лежит между 63 = 216 и 73 = 343, кубический
корень находится в районе 60> (так как 603 = 216 000 и 703 = 343 000).
Следовательно, первая цифра кубического корня будет 6
✴ Для определения последней цифры кубического корня, заметьте, что только число 8 обладает кубом, оканчивающимся на 2 (83 = 512), так что последняя цифра оканчивается на 8.
Поэтому кубический корень 314 432 будет 68. Три простых шага и вы на месте. Обратите внимание, что какждая цифра от 0 до 9 появляется по одному разу в виде последней цифры куба. (В действительности, последняя цифра кубического корня равна последней цифре куба последней цифры куба. Попробуй разберись!)
А теперь попробуйте для практики:
Какой кубический корень 19 683?
◉ 19 находится между 8 и 27 (23 и 33)
◉ Следовательно, кубический корень где-то в районе 20>
◉ Последняя цифра в задаче 3, что соответствует 343 = 73,
значит 7 - это последняя цифра Ответ 27.
Обратите внимание, что наши выводы по поводу последней цифры работают, только если исходное число - кубический корень для целого числа. Например, кубический корень 19 684 бует 27,0004572 . . . Определённо не 24 . Вот почему включили это в раздел математической магии, а не в более ранние главы. (Кроме того, расчёты такие быстрые, что кажется, будто без магии не обошлось!)
Упрощенные квадратные корни
Квадратные корни также могут быть легко посчитаны, если вам задали полный квадрат. Например, если кто-то сказал вам, что квадрат двузначного числа будет 7569, то вы в состоянии мгновенно ответить, что исходное число (квадратный корень) это 87. Вот как:
◆ Посмотрите на величину сотен (цифры, предшествующие
последним двум), 75 в данном примере
◆ Так как 75 находится между 82 (8 х 8 = 64) и 92 (9 х 9 = 81), то нам известно, что квадратный корень будет где-то в районе 80>. Следовательно, первая цифра квадратного корня будет 8. Существует два числа, чьи квадраты заканчиваются на 9: 32 = 9, 72 =
49. Так что последня цифра должна быть 3 или 7. Таким образом, квадратный корень либо 83, либо 87. Какой из них?
◆ Сравните исходное число с квадратом 85 (который мы можем
легко посчитать как 80 х 90 + 25 = 7225). Так как 7569 больше, чем
7225, квадратный корень будет большим числом, 87.
Давайте решим ещё один пример.
Какой квадратный корень 4761?
Так как 47 лежит между 62 = 36 и 72 = 49, ответ должен быть в районе 60>. Раз уж последняя цифра квадрата есть 1, то последняя цифра квадратного корня должна быть 1 или 9. Так как 4761 больше, чем 652 = 4225, то квадратный корень должен быть 69. Как и с
предыдущим трюком для кубического корня, этот метод может быть использован, только когда исходное число даёт полный квадрат.
Удивительная сумма
Следующий трикс впервые был показан мне Джеймсом
«Удивительным» Рэнди, который его эффективно использовал в своей магии. Здесь волшебник может предсказать сумму четырёх случайно выбранных трёхзначных чисел.
Дабы подготовить данный фокус, вам понадобятся три комплекта колод из девяти карт каждая и кусок бумаги с записанным числом 2247 на нём, который вы запечатаете в конверт. Далее, над каждым комплектом карт произведите следующие действия:
★ На колоде А запишите следующие цифры (одно на каждую
карту):

★ На колоде В запишите следующие числа:

★ На колоде С запишите следующие числа:

Выбирете трёх человек из аудитории и дайте каждому колоду карт. Пусть каждый из ваших добровольцев наугад выберет одну из девяти карт, которые они держат в руках. Допустим, они выбрали числа 4286, 5792 и 5435. Теперь, соблюдая последовательность, пусть каждый громко назовёт одну из цифр четырёхзначного числа: сначала человек А, потом человек В и, наконец, человек С. Скажем, они
назвали цифры 8, 9 и 5. Запишите цифры 8, 9 и 5 (895) и скажите: «Вы должны признать, что данное число было выбрано полностью наугад и не могло быть возможности заранее предсказать его».
Далее, пусть три человека выкрикнут другие цифры со своих карт. Скажем, были названы 4, 5 и 3. Запишите 453 ниже числа 895. Затем повторите данную процедуру ещё два раза для двух оставшихся чисел, получив в итоге четыре трёхзначных числа, что-то вроде:
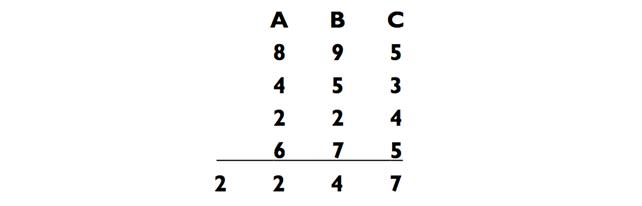
После пусть кто-нибудь сложит эти четыре числа и озвучит сумму. А дальше пусть кто-нибудь откроет конверт, дабы показать ваше предсказание. Наслаждайтесь аплодисментами!
Почему это работает
Взгляните на числа на картах каждой из колод и посмотрите, сможете ли вы найти каку-либо последовательность. Каждый набор чисел в сумме даёт одинаковую величину. Набор чисел А при сложении даёт 20. Набор В - 23. Набор С - 17. С цифрами из колоды
«С», которые в правом столбике дают в сумме 17, вы всегда будете записывать 7 и переносить 1. С числами из колоды «В», которые в сумме дают 23 (плюс 1), вы всегда будете записывать 4 и переносить 2. Наконец, с числами из колоды «А», которые в сумме дают 20, после прибавления 2 вы получите общий итог 2247!
День для любой даты
Мы завершим нашу книгу одним из проверенных временем подвигов ментальных калькуляций: как узнать на какой день недели приходится чей-либо день рождения. Это действительно очень практичный навык. Не каждый денькто-то будет просить вас возвести в квадрат трёхзначное число, но едва ли один день проходит без того, что кто-то упоминает дату из прошлого или будущего. Всего лишь немного практики, и вы сможете быстро и легко определять день недели практически любой исторической даты. Сначала мы присвоим кодовый номер каждому дню недели. Их легко запомнить:
| ПОНЕДЕЛЬНИК | ВТОРНИК | СРЕДА | ЧЕТВЕРГ | ПЯТНИЦА | СУББОТА | ВОСКРЕСЕНИЕ |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 или 0 |
Далее нам понадобится код для каждого месяца. Коды будут использоваться для каждого года за двумя исключениями. Во время високосного года (например, 2000-2004-2008 и так далее) код месяца для Января будет 5, а для Февраля 1.
| Январь | Февраль | Март | Апрель | Май | Июнь | Июль | Август | Сентябрь | Октябрь | Ноябрь | Декабрь |
| 6 (5) | 2 (1) | 2 | 5 | 0 | 3 | 5 | 1 | 4 | 6 | 2 | 4 |
Теперь давайте вычислим день недели для любой даты в 2006 году. После этого, мы опишем 2007, затем 2008, и так далее, до конца вашей жизни. Когда все даты из будущего будут разобраны, мы сможем заглянуть назад в прошлое и определить дни недели для любой даты из 1900-ых или любого другого века.
Каждому году присвоен кодовый номер, и в случае 2006 года таковым будет 0 (см. страницу).
Теперь, чтобы вычислить день недели, вы просто складываете код месяца плюс код даты плюс код года. Таким образом, для 3 Декабря 2006 года, мы рассчитываем
Код месяца + Дата + Код года = 4 + 3 + 0 = 7
Следовательно, эта дата приходится на День 7, что есть Воскресенье.
Как на счёт 18 Ноября 2006? Так как Ноябрь имеет код месяца 2,
мы имеем
Код месяца + Дата + Код года = 2 + 18 + 0 = 20
Теперь, раз уж неделя повторяется каждые семь дней, мы можем отнять любое кратное 7 от нашего ответа (7, 14, 21, 28, 35, . . .) и это никак не повлияет на день недели. Итак, наше заключительное действие представляет собой вычитание наибольшего кратного 7, чтобы получить 20 - 14 = 6. Следовательно, 18 Ноября 2006 года выпадает на Субботу.
Как на счёт 2007? Ну, что происходит с днём вашего рождения, когда вы переходите от одного года к следующему? Большинство из них состоит из 365 дней, и, так как 364 кратно 7 (7 х 52 = 364), то день недели вашего рождения передвинется вперёд на один (в случаях, когда 1 год = 365 дней). Если между вашими днями рождения 366 дней, тогда день недели вашего рождения передвинется на два вперёд. Следовательно, для 2007 года мы вычислили день недели как и раньше, но сейчас мы использовали код года 1. Далее, 2008 - високосный год. (Високосный год приходится на каждый четыре года, так что 2000, 2004, 2008, 2012, . . . , 2096 - високосные года двадцать первого века) Отсюда, для 2008, код года увеличивается на два, так что он теперь будет 3. Следующий год, 2009, не является високосным, так что код увеличивается на 1 (и будет 4).
Таким образом, 2 Мая 2007 года, например, будет
Код месяца + Дата + Код года = 0 + 2 + 1 = 3
так что эта дата приходится на Среду.
Для 9 Сентября 2008 года мы имеем
Код месяца + Дата + Код года = 4 + 9 + 3 = 16
Отнимая наибольшее кратное 7, мы получаем 16 - 14 = 2, так что дата приходится на Вторник.
С другой стороны, 16 Января 2008 года - високосный период, так что код месяца будет 5, вместо 6. Мы имеем
Код месяца + Дата + Код года = 5 + 16 + 3 = 24
и вследствие этого приходится на день 24 - 21 = 3, который является Средой. Для справки, мы перечислили все коды для каждого года двадцать первого века на рисунке на следующей странице. Хорошая новость заключается в том, что вам не нужно запоминать данную таблицу. Мы может устно посчитать код года для любой даты в промежутке от 2000 до 2099. Для определения кода 2000 + x, мы просто берём число х/4 (игнорируя остаток) и прибавляем частное к х. Код года может быть сокращён путём вычитания из него кратного 7. Например, в случае с 2061, мы видим, что 61/4 = 15 (с остатком 1, который мы не учитываем). Таким образом, 2061 имеет код года в размере 61 + 15 = 76. И раз уж мы можем отнять любое кратное 7, то давайте используем упрощённый код года в виде 76 - 70 = 6.
Дата: 2018-12-21, просмотров: 487.