
Умно ж ение «3- на -2»
Мы уже видели во время решение задачек типа «2-на-2», что существует несколько разных путей решения одного и того же примера. Многообразие методов увеличивается, когда вы увеличиваете количество цифр в задаче. При умножения «3-на-2» я нахожу выгодным «предварительный осмотр» примера для определения метода расчёта, который подвергнет мозг наименьшей нагрузке.
Факторинговый метод
Самые лёгкие задачи «3-на-2» это те, в которых двузначные числа можно разложить.
Например:
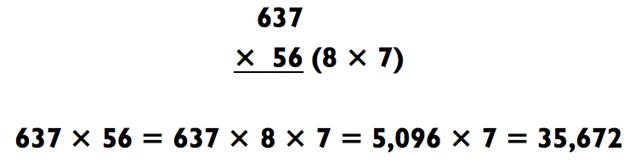
Они потрясные, потому что вам не нужно ничего прибавлять. Вы просто раскладываете 56 как 8 х 7, затем решаете пример «3-
на-1» (637 х 8 = 5096) и, наконец, пример «4-на-1» (5096 х 7 = 35 672).
Больше нет никаких дополнительных действий, и отсутствует нужда в запоминании промежуточных результатов.
Больше половины всех двузначных чисел можно разложить на числа типа 11 и ниже, так что вы будете в состоянии использовать данный метод для многих задач. Вот пример:
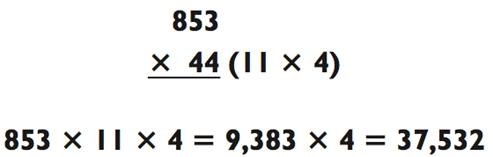
Чтобы умножить 853 х 11, представьте 853 в виде 850 + 3 и продолжайте в следующем ключе:
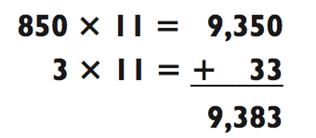
Теперь умножьте 9383 х 4, представив 9383 как 9300 + 83
следующим образом:
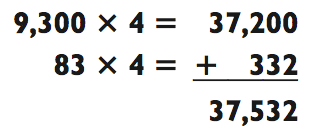
Если двузначное число не раскладывается на меньшие числа, изучите трёхзначное на предмет такой возможности:
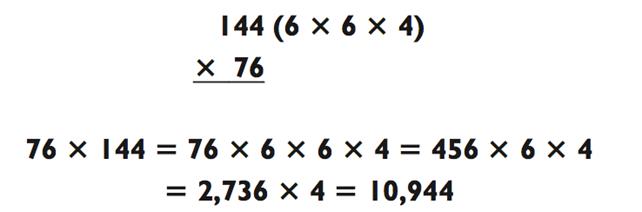
Обратите внимание на то, что последовательность умножения выстроилась из задач «2-на-1», «3-на-1» и, наконец, «4-на-1». Раз уж это все те задачи, которые сейчас уже можете решать значительной легкостью, такой тип задач «3-на-2» в принципе не должен стать проблемой для вас.
Вот ещё один пример, где двузначное число не подвергается факторизации, но зато трёхзначное число - да:
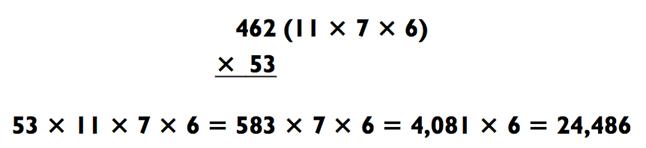
Здесь последовательность «2-на-2», «3-на-1» и «4-на-1», хотя, когда трёхзначное число разлагается на 11, вы можете использовать метод умножения на 11 и получить легкий пример «2-на-2» (53 х 11 = 583). В данном случае, признание возможности разделить число на 11 оправдывает себя (как было описано в Главе 4).
Если двузначное число не раскладывается, а трёхзначное раскладывается только в виде «2-на-1», с задачей всё ещё можно легко найти общий язык путём умножения «2-на-2», а затем «4-на-1»:
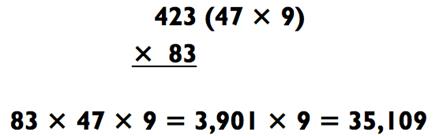
Здесь вам необходимо будет увидеть то, что 423 делится на 9, ставя перед нами задачу 83 х 47 х 9. Такая задача «2-на-2» не такая уж и простая, но если представить 83 как 80 +3, то вы получите:
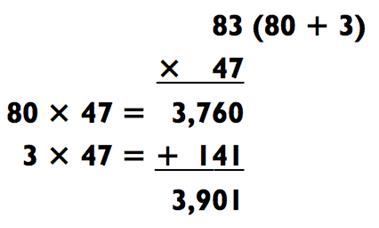
Затем решите задачу «4-на-1» в виде 3901 х 9 для получения итогового ответа в размере 35 109.
Метод сложения
Если двух и трёхзначное числа в задаче «3-на-2» не поддаются простому разложению, вы всегда можете прибегнуть к методу сложения:

Данный метод требует от вас сложения результатов задачи «2- на-2» и «2-на-1». Такого рода задачи имеют в себе более сожные элементы (нежели те, которые могут быть факторизованы) так как вы вынуждены решить пример «2-на-1», держа в уме пятизначное число, а затем сложить результаты вместе. В действительности, возможно даже будет проще решить эту задачу путём разложения 721 как 103 х 7 и последующего вычисления 37 х 103 х 7 = 3811 х 7 = 26 677.
Вот другой пример:

Хотя вы обычно будете разбивать трёхзначное число во время использования метода сложения, порой разбитие двузначного числа вместо этого бывает более выгодным, в особенности когда последние цифры двузначного числа это 1 или 2, как в следующем примере:
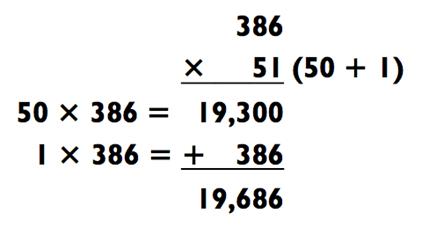
Это сокращает «3-на-2» до «3-на-1», делая нашу задачу особенно лёгкой, так как второе действие на умножение включает 1. Заметьте также, что нам была оказана помощь в виде умножения 5 на чётное число, что принесло дополнительный 0 в ответ, так что только одна цифра перекрывается в задаче на сложение.
Другой пример умножения 5 на чётное число проиллюстрирован на следующей задаче:
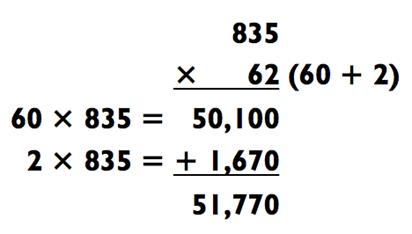
Когда вы умножаете 6 (из 60) на 5 и получаете 835, это порождает появление дополнительного 0 в ответе, делая задачу на сложение в особенности лёгкой.
Метод вычитания
Как и с примерами «2-на-2», бывает иногда проще решить задачу
«3-на-2» путём вычитания вместо сложения, как в следующих задачках:
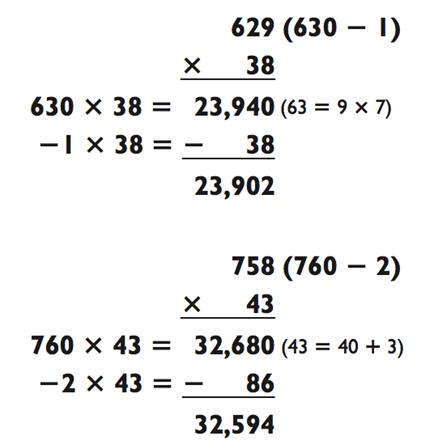
В отличии от этого, вы можете сравнить методы вычитания и сложения ниже, применив их к одной и той же задаче:
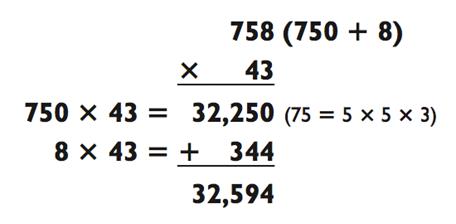
Мое предпочтение при решении данной задачи - использование метода вычитания, потому что я всегда стараюсь оставить себе максимально лёгкую задачу на сложение или вычитание на самый конец. В данном случае, я бы лучше вычел 86, чем прибавил 344, даже при том, что решение задачи типа «2-на-2» (см. выше) методом вычитания слегка тяжелее, чем методом сложения.
Метод вычитания также может быть использован с трёхзначными числами, которые меньше кратного 100 или близки к кратному 1000, как в следующих двух примерах:
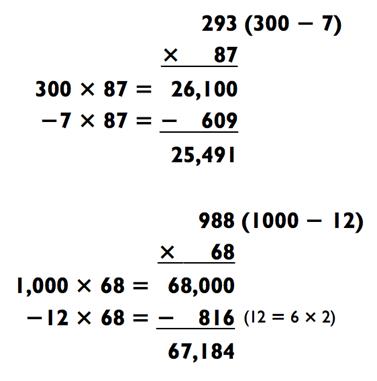
Последние три цифры ответа были получены путём использования дополнений 609 - 100 = 509 и 816, соответственно.
Наконец, на следующей иллюстрации мы поделили двузначное число с помощью метода вычитания. Обратите внимание, как мы отняли 736 путём вычитания 1000 и обратного прибавления дополнения:
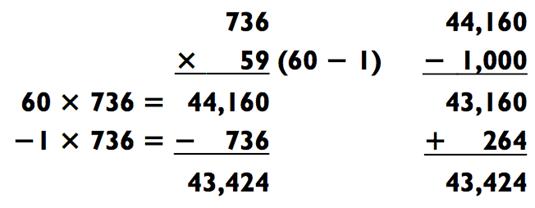
Дата: 2018-12-21, просмотров: 426.