Умно ж ение «3- на -3»
На пути к продвижению к нашему грандиозному финалу в виде умножения «5-на-5», задачки типа «3-на-3» наше последний барьер. Как и в случае с «3-на-2», существует многообразие методов, которые могут быть использованы для упрощения процесса в целом.
Метод факторинга
Мы начнём с метода факторинга. К несчастью, большинство трёхзначных чисел не раскладываются на единичные цифры, но если всё-таки раскладываются, процесс вычисления будет не таким уж и плохим.
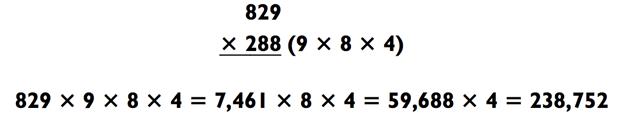
Обратите внимание на последовательность действий. Вы упрощаете задачу «3-на-3» (829 х 288) до «3-на-1-на-1-на-1». путём разложения 288 на 9 х 8 х 4. Далее это превращается в «4-на-1- на-1» (7461 х 8 х 4) и, наконец, в «5-на-1» для получения итогового ответа 238 752. Прелесть данного процесса заключается в отсутствии каких-либо действий на сложение и в том, что ничего не нужно хранить в памяти. Когда вы получили пример «5-на-1», то встали в одном шаге от выполнения задания.
Задача типа «5-на-1» может быть решена в два действия, если принять 59 688 как 59 000 + 688, а затем сложить результаты задач «2-
на-1» (59 000 х 4) и «3-на-1» (688 х 4), как показано ниже:
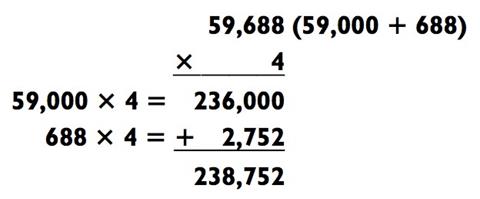
Если оба трёхзначных числа могут быть разложены как «2-на-1», тогда задача «3-на-3» может быть упрощена до «2-на-2-на-1-на-1», как в следующей задаче:
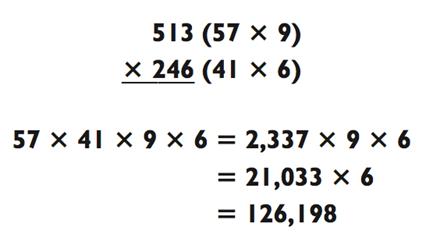
Как обычно, лучше всего сразу избавиться от тяжёлого элемента задачи (2-на-2). Как только вы сделали это, она будет сведена к «4- на-1», а затем к «5-на-1».
Почти всегда, только одно из чисел будет раскладываться. В таком случае, можно будет свести задачу к «3-на-2-на-1», как в следующем примере:
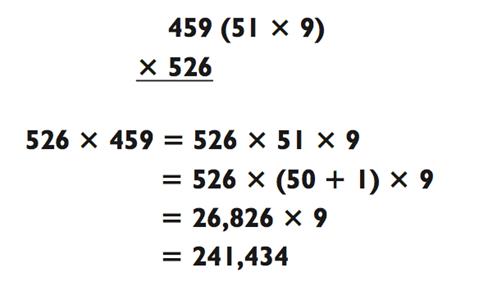
Следующая задача «3-на-3», в действительности, просто замаскированная «3-на-2»:
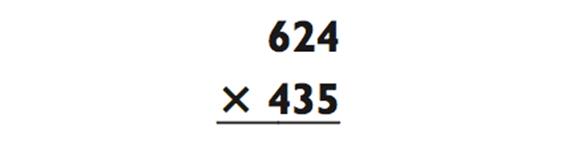
Путём удвоения 435 и сокращения 624 на половину, мы получаем эквивалентную задачу:
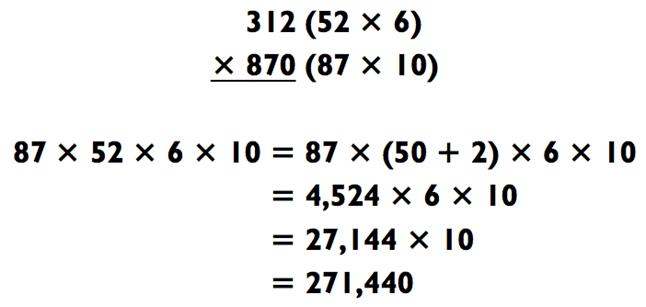
Метод совместной близости
Вы готовы к кое-чему полегче? Следующая «срезка», которую мы представили в Главе 0, основана на следующей алгебраической формуле:
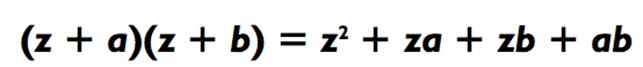
Что мы переписываем как:
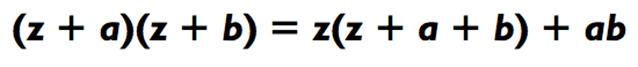
Эта формула правомерна для любых значений z, a и b. Мы будем пользоваться этим всякий раз, когда трёхзначные числа, которые нужно перемножить (z х a и z х b), находятся близко к лёгкому числу z (типичный случай - число с кучей нулей). Например, умножим:
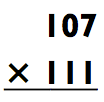
Мы будем рассматривать эту задачу как (100 х 7)(100 х 11).
Благодаря использованию z х 100, a х 7, b x 11 наша формула даёт нам:
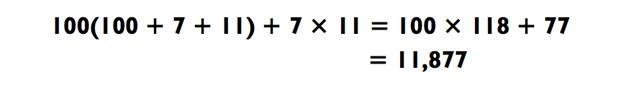
Я схематически изобразил задачу вот так:
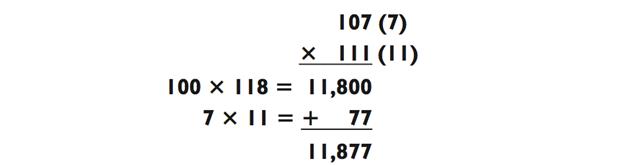
Цифры в скобках обозначают разницу между числом и нашим удобным «базовым числом» (здесь, z = 100). Число 118 может быть получено либо через сложение 107 + 11, либо через 111 + 7. По законам алгебры, обе эти суммы эквивалентны, так как (z x a) b (z x b) a.
В этот раз без лишней болтовни, вот вам ещё одна «ускорялка»:
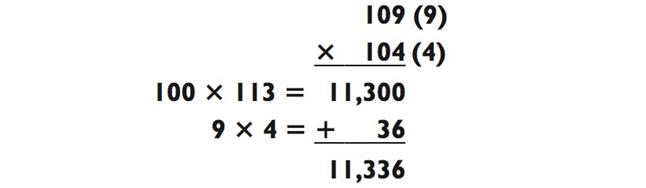
Всё чётко!
Давайте слегка поднимем ставке и возьмём базовое число побольше.
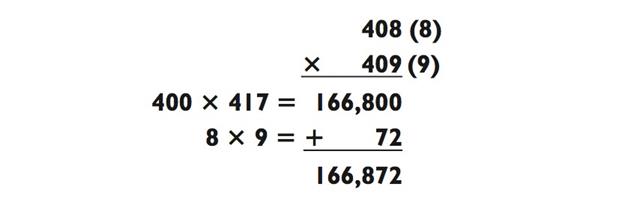
Хотя данный метод обычно и используется для умножения трёхзначных чисел, мы также можем применить его для задачи «2- на-2»:
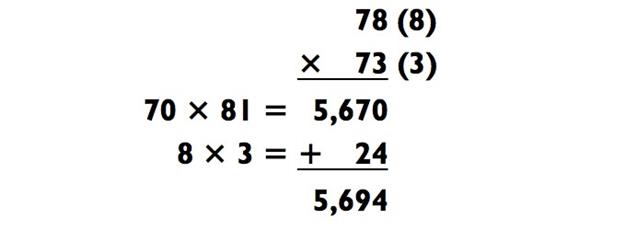
Здесь базовое число 70, его мы умножаем на 81 (78 + 3). Даже действие на сложение обычно очень простое.
Мы также можем применить данный метод, когда два числа оба меньше, чем базовое. Как, например, в следующей задачке, где оба числа меньше 400:
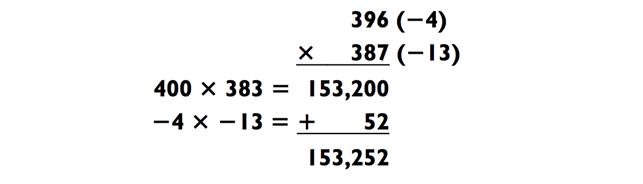
Число 383 может быть получено действием 396 - 13, или 387 - 4. Я буду использовать данный метод для задач типа «2-на-2», таких как эти:
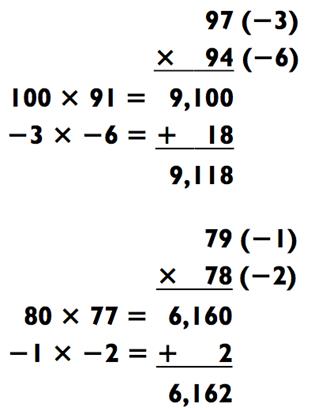
В нашем следующем примере базовое число находится между перемножаемыми числами:
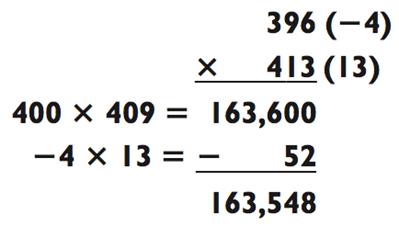
Число 409 получено по результатам 396 + 13, или 413 - 4. Обратите внимание, что с тех пор, как -4 и 13 имеют противоположные знаки, мы должны вычесть 52.
Давайте поднимем ставки ещё выше, до уровня, где второе действие требует умножения «2-на-2»:
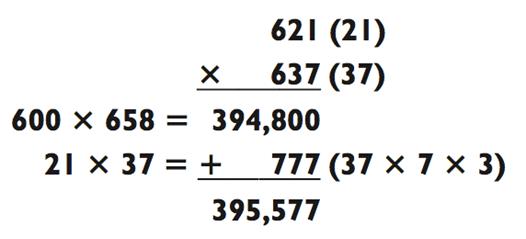
Здесь мы обращаем внимание на то, что первое действие в задачке (600 х 658) уже само по себе является разумной оценкой. Наш метод позволяет вам перейти от оценки к точному ответу.
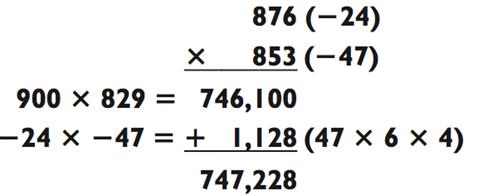
Также обратите внимание, что во всех этих примерах числа, которые мы перемножаем в первом действии, обладают такой же суммой, как и исходные числа. Например, в задачке выше, 900 + 829 = 1729, как и 876 + 853 = 1729. Это потому, что:
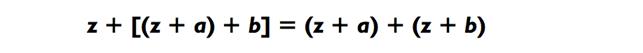
Следовательно, чтобы получить число, которое будет умножено на 900 (которое, как вы знаете, будет в районе 800>), вам всего лишь нужно взглянуть на последние две цифры 76 х 53 = 129, чтобы определить 829.
В следующем примере, сложение 827 + 761 = 1588 подсказывает нам, что следует просто умножить 800 х 788, а затем вычесть 27 х 39 следующим образом:
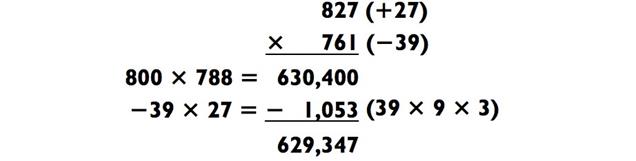
Этот метод настолько эффективен, что если задача «3-на-3», над которой вы сидите в настоящий момент, состоит из чисел далёких друг от друга, то вы можете иногда видоизменить проблему путём деления одного и умножения другого чисел на одинаковую величину (тем самым приблизив их друг к другу). Например, задача 672 х 157 может быть решена так:
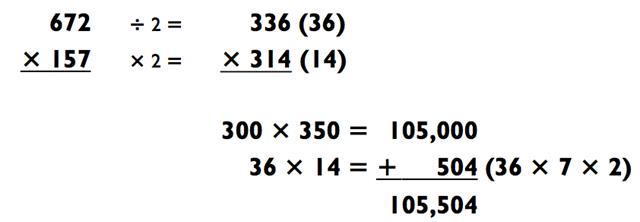
Когда умножаемые числа одинаковые (ближе друг к другу уже некуда!), обратите внимание, что вычисления методом «close-together» генерируют в точности такие же вычисления, какие вы выполняете во время традиционной процедуры возведения в квадрат:
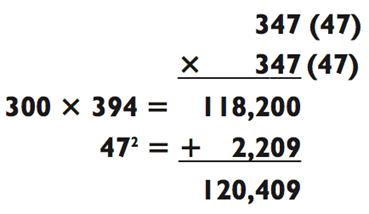
Метод сложения
Когда ни один из предыдущих методов не работает, я ищу возможность использовать метод сложения, в особенности, когда первые две цифры одного из трёхзначных чисел легки в обращении. Например, в задаче ниже, «64» из 641 раскладывается на 8 х 8, так что я бы решил её следующим образом:
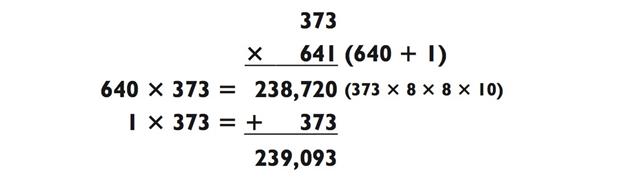
Схожим образом, в следующем примере «42» из 427 раскладывается как 8 х 8, так что вы можете использовать метод сложения и представить 427 в виде 420 + 7:
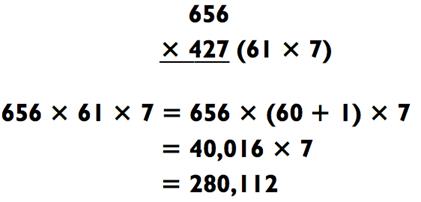
Часто я разбиваю последнюю задачку на сложение на два этапа, как здесь:
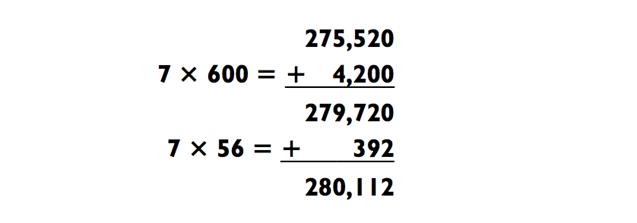
Так как задачки, которые могут быть решены методом сложения, требуют определённых усилий, я обычно сворачиваю с данной дорожки с целью найти способ, который в результате приведёт к простым вычисления в концовке. Например, задача выше могла быть решена с использованием факторинга. По сути, вот какое бы я выбрал решение:
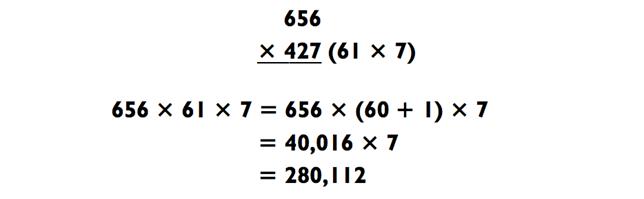
Самые простые задачи, которые могут быть решены методом сложения, содержат одно число с 0 в середине, как показано ниже:

Такие задачи, как правило, намного проще, чем другие, которые тоже можно решить таким способом. Так что стоит вглядываться в пример «3-на-3» на предмет его конвертации в такую задачу. Это окупается. Например, 732 х 308 можно было бы получить с помощью любого из «безнулевых» примеров ниже:

Мы упоминали, что другой способ решения данной задачи состоит в действии 308 х 366 х 2, и использовании преимущества близости нахождения 308 и 366. Давайте прорешаем ещё «крепкий орешек»:
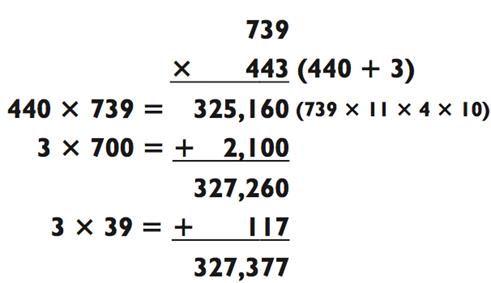
Метод вычитания
Метод вычитания - то самое орудие, которое я время от времени использую, когда одно из трёхзначных чисел может быть округлено до простого двузначного число с 0 на конце, как в следующем примере:
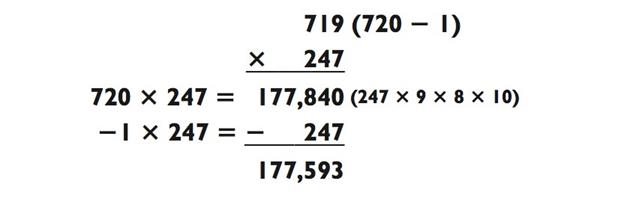
Аналогично в следующей задачке:
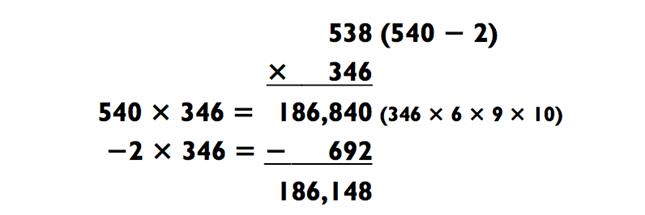
Дата: 2018-12-21, просмотров: 464.