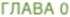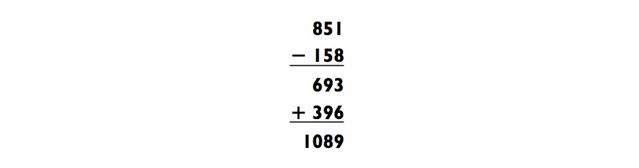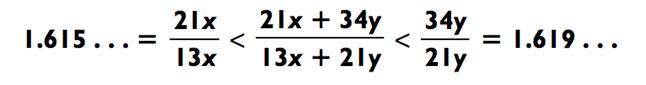|
Фокусничаем: искусство матемагии
Я всегда получал удовольствие от игры с цифрами. Я нахожу арифметику такой же занимательной как магия. Но понимание магических секретов арифметики требует знаний в алгебре. Конечно, есть и другие причины для её изучения. Назову лишь несколько из них: сдача экзаменов, моделирование проблем из реального мира, программирование и возможность понимания высшей математики. Но что первое заинтересовало меня в алгебре, так это желание понять некоторые матемагические трюки, которые я сейчас представлю вам!
Экстрасенсорная математика
Скажите добровольцу в аудитории: «Загадайте число, любое число». Вам также следует произнести: «Но чтобы не утруждать себя, придумайте число из одной-двух цифр». После того, как вы напомнили добровольцу, что вы никоим образом не можете знать число у него в голове, попросите следующее:
➡ Удвойте число
➡ Прибавьте 12
➡ Разделите сумму на 2
➡ Вычтите из неё исходное число
Затем скажите: «Думаете ли вы сейчас о цифре 6?» Опробуйте это сначала на себе и вы увидите, что данная последовательность всегда в итоге приводит к цифре 6, несмотря на то, какое число было изначально выбрано.
Почему это работает
Данный трюк целиком основан на простой алгебре. В действительности, я иногда использую его как способ представить алгебру студентам. Секретное число, которое выбирает ваш волонтёр,
|
(в том порядке, в котором вы их совершали):
✓ 2Х (удвоить число)
✓ 2Х + 12 (прибавить 12)
✓ (2Х + 12)/2 = Х + 6 (разделите на 2)
✓ Х + 6 - Х (вычтите исходное число)
Так что неважно, какое число выберет доброволец: итоговый ответ всегда будет 6. Если вы будете повторять данный приём, попросите добровольца прибавить другое число на втором шаге (скажем, 18). Итоговый ответ будет половиной этого числа (а именно 9).
Магическое 1089!
А вот трикс, существующий уже который век. Сделайте так, чтобы человек из аудитории достал ручку с бумагой и:
Тайно записал трёхзначное число, цифры которого идут в порядке уменьшения (как 851 или 973).
Перевернул число задом наперёд и отнял это значение из исходного числа
Полученный ответ прибавил к исходному числу, записанному задом наперёд
В конце последовательности, магическим образом появится ответ 1089, несмотря на то, какое число выбрал ваш доброволец. Например:
Почему это работает
Неважно, какое трёхзначное число вы или кто-либо другой выберете в этой игре, окончательный ответ всегда будет 1089. Почему? Обозначим АВС как неизвестное трёхзначное число. Алгебраически, это равняется:
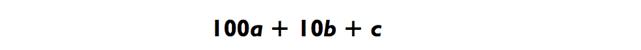
Когда вы переворачивает число и вычитаете его из исходника, то получаете число СВА, которое алгебраически равно:
После вычитания СВА из АВС, вы получаете:
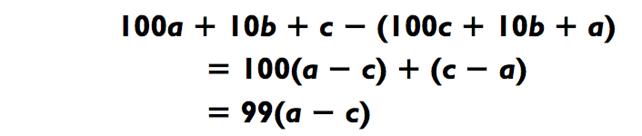
Следовательно, после вычитания на шаге 2, мы должны получить одно из следующих кратных 99: 297, 396, 495, 594, 693, 792 или 891, каждое из которых в итоге даст 1089 после прибавления к нему своей перевёрнутой версии, как мы и поступаем на шаге 3.
Трюк с пропущенной цифрой
Используя 1089 из прошлого действия, вручите добровольцу калькулятор и попросите его умножить 1089 на трёхзначное число (на
его вкус), но не говорить вам, что это за число. (скажем, он тайно умножит 1089 х 256 = 278 784) Теперь спросите, сколько цифр в полученном ответе. Ответ будет: «Шесть».
Дальше вы говорите: «Громко назовите пять из этих шести цифр в любом порядке. Я попытаюсь определить недостающую». Предположим, волонтёр выкрикивает: «Два…четыре…семь…восемь… восемь». Вы вежливо говорите ему, что он пропустил цифру 7. Секрет основан на том факте, что число кратно 9 тогда, и только тогда, когда его цифры в сумме дают кратное 9. Так как 1 + 0 + 8 + 9 = 18 кратно 9, значит и 1089 кратно 9. Таким образом, 1089 при умножении на любое целое число даст кратное 9. И раз уж прозвучавшие цифры в сумме дают 29, и следующее кратное 9, которое больше 29, это 36, то наш доброволец должно быть не учёл число 7 (так как 29 + 7 = 36). Есть более утончённые способы заставить добровольца в конечном итоге прийти к кратному 9. Вот некоторые из моих любимых:
Пусть он наугад выберет шестизначное число, перемешает его цифры, затем отнимет меньшее из шестизначных чисел из большего. Так как мы производим вычитание двух чисел с одинаковой модульной суммой (в самом деле, сумма цифр идентична), полученная в итоге разница будет иметь модульную сумму в размере 0, и, следовательно, число будет кратно 9. Далее продолжайте как и раньше, чтобы найти недостающую цифру.
Пусть он тайно выберет четырёхзначное число, перевернёт его задом наперёд, а потом вычтет меньшее из чисел из большего. (получится кратное 9) Затем пусть умножит полученное число на 3, а вы продолжайте как и раньше.
Попросите его умножать цифры друг на друга до тех пор, пока их произведение не превратится в семизначное число. Это будет не «гарантированное» кратное 9, но на практике так получается не меньше, чем в 90% случаев (шансы высоки, что перемножаемые цифры будут включать 9-ки или две 3-ки, или две 6-ки, или 3 и 6). Я часто использую данный способ, когда выступаю перед математически продвинутой аудиторией, которая может раскусить другие методы.
Существует кое-какая проблема, за которой нужен глаз да глаз. Предположим, прозвучавшие числа в сумме дают кратное 9 (скажем, 18). После такого у вас не будет возможности определить, пропущен ли 0 или 9. Как исправить это? Легко - сжульничайте! Просто скажите:
«Вы ведь не пропустили 0, не так ли?» Если был пропущен 0, то вы успешно провернули свой трюк. Если нет, то скажите: «Оу, просто казалось, будто в голове у вас пусто! Вы не пропустили один, два, три или четыре, не так ли?» Доброволец либо покачает головой, либо скажет «нет». Затем вы продолжаете: «Как и не пропустили вы пять, шесть, семь или восемь. Вы не включили девять, не так ли?» Доброволец ответит утвердительно, и вы получите ваши заслуженные аплодисменты!
Сложение-чехарда
Данный приём сочетает в себе быстрые ментальные вычисления и поразительные предсказания. Вручите зрителю карту с десятью линиями на ней, пронумерованными от 1 до 10. Пусть зритель загадает два положительных числа от 1 до 20 и подпишет ими линии 1 и 2.
Далее попросите его записать сумму 1 и 2 линий на линии 3. Затем сумму линии 2 и 3 на линии 4, и так далее, как проиллюстрировано ниже.
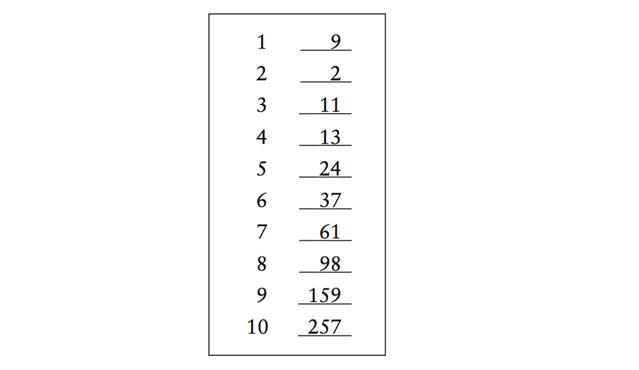
Наконец зритель показывает вам карту. Вы сразу же можете сказать ему сумму всех чисел на карточке. Например, в нашем случае, вы могли бы мгновенно объявить, что числа в сумме дают 671, даже быстрее, чем зритель сделал бы это с калькулятором. В качестве
«нежданчика», вручите зрителю калькулятор и и попросите его разделить число на линии 10 на число с линии 9. В нашем примере, частное 257/159 = 1,616. Пусть он озвучит первые три цифры частного, а после перевернёт карточку (там вы уже написали своё предсказание). Зритель будет очень удивлён тому, что вы уже записали число 1,61!
Почему это работает
Для проведения быстрых вычислений вам просто нужно умножить число с линии 7 на 11. Здесь 61 х 11 = 671. Причина, по
|
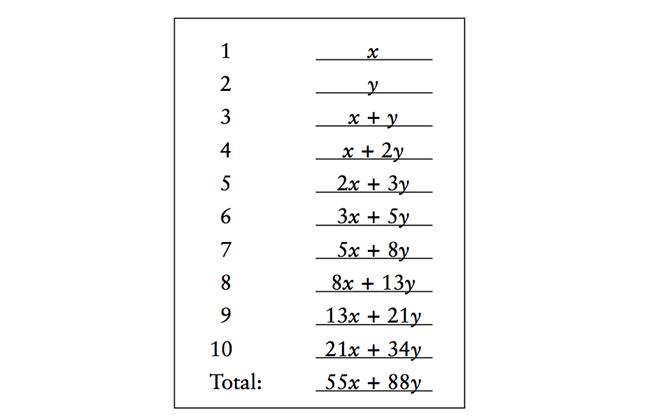
Что касается предсказания, мы используем тот факт, что для любого положительного числа (a, b, c, d), если a/b < c/d, дробь, которую вы получите путём «ошибочного сложения дробей» (например, сложение числителей и сложение знаминателей), будет находиться между двумя исходными дробями. То есть,
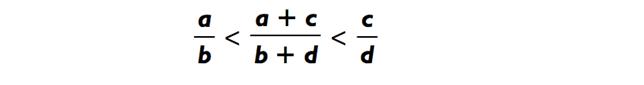
Таким образом, частное линии 10, делённой на линию 9, (21х + 34у)/(13х + 21у), должно лежать между
Следовательно, пропорция должна начинаться с цифр 1,61, как и было предсказано.
По сути, если вы продолжите такую «чехарду» вплоть до бесконечности, отношение последовательно идущих значений будет подбираться все ближе и ближе к
числу с таким огромным количеством удивительно красивых и загадочных свойств, что его часто называют золотое отношение (золотое сечение).
Магичиские квадраты
Вы готовы к испытанию совершенно другого порядка? Ниже вы найдёте то, что называют «магичиский квадрат». Столько всего было написано на данную тему и о том, как составлять их (вплоть до времен Древнего Китая). Здесь мы описываем способ презентации магических квадратов в развлекательном стиле. Вот заученная схема, которую я исполнял годами.
Я показываю визитку со следующей надписью на задней стороне:
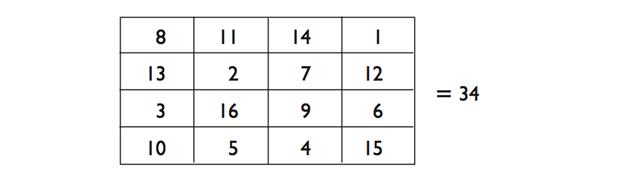
Я говорю : «Это называется магический квадрат. По сути, это самый маленький магический квадрат, который вы можете создать, используя числа от одного до шестнадцати. Вы заметите, что каждая строка и каждый столбец при сложении всех элементов дают одно и то же число - тридцать четыре. Сейчас, когда я провёл такое обширное исследование на тему магических квадратов, я предлагаю создать один для вас прямо у вас на глазах».
Затем я прошу кого-либо из аудитории дать мне любое число больше 34. Давайте предположим, что мне назвали 67.
|
Я продолжаю: «В случае с первым магическим квадратом, каждая строка и каждый столбец при сложении давали тридцать четыре. (на данной стадии, я обычно откладываю карточку с этим квадратом в сторону) Давайте посмотрим, что у нас получилось с новым квадратом». После проверки того, что кадая строка и каждый столбец в сумме равняются 67, я говорю: «Но я не останавливаюсь на этом. Специально для вас, я решил зайти ещё на один шаг дальше. Обратите внимание, обе диагонали при сложении дают шестьдесят семь!» Затем я указываю, что четыре квадратика в левом верхнем углу
в сумме дают 67 (16 + 19 + 22 + 10 = 64), как и все остальные строки и столбцы такого размера! «Они все в сумму равны шестидесяти семи. Но не верьте мне наслово. Пожалуйста, оставьте себе магический квадрат в качестве сувенира от меня и проверьте его потом сами!»
Дата: 2018-12-21, просмотров: 375.
