Вы можете создать магический квадрат, который бы при суммирование давал любое число, воспользовавшись с выгодой для себя исходным магическим квадратом, который в сумме даёт 34. Держите его на виду, когда создаёте новый для добровольца. Пока вы чертите сетку 4-на-4, устно выполните вычисления для шагов 1 и 2:

Вычтите 34 из заданного числа (например, 67 - 34 = 33)

Разделите полученное число на 4 (например, 33/4 = 8 с остатком 1)

Частное есть первое «магическое» число. Частное плюс остаток есть второе «магическое» число. (здесь наши магические числа 8 и 9)

Когда доброволец показывает на клетку, незаметно взгляните на квадрат-34 и посмотрите, какой квадратик является корреспондирующим. Если это 13, 14, 15 или 16, прибавьте второе число (в нашем примере, 9). Если нет, то прибавьте первое магическое число (8)

Вставляйте подходящее число до тех пор, пока не закончите составление магического квадрата

Обратите внимание: когда заданное число - чётное, но не кратное 4, то ваши первое и второе магические числа будут одинаковыми. Так что у вас будет только одно магическое число для прибавления его к числам из квадрата-34.

Почему это работает

Причина, по которой данный метод работает, основана на том факте,  что  каждая  строка,  столбец,  диагональ  из  изначально

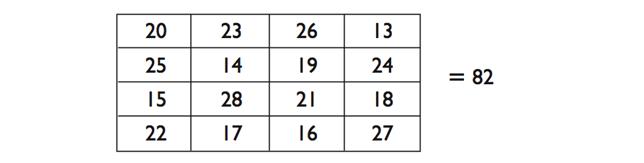
показанного магического квадрата при сложение даёт 34. Предположим, заданное число 82. Так как 82 - 34 = 48 (и 48/4 = 12), мы будет  прибавлять  12  к  каждому  числу  в  квадратике.  Затем  каджая

«группа четвёрок», которая до этого равнялась 34, будет при сложении давать 34 + 48 = 82. Рассмотрите магический квадрат ниже.

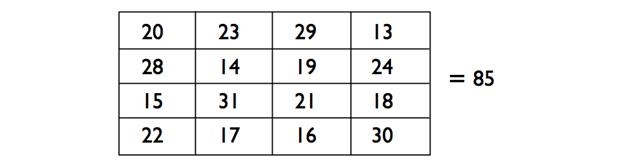
С другой стороны, если заданное число было бы 85, наши магические числа были бы 12 и 15. Так что нам мы бы прибавляли на 3 больше к квадратикам, которые содержат числа 13, 14, 15 и 16. Так как каждая строка, столбец и группа четвёрок содержит в точности одно из этих чисел, каждая группа четвёрок теперь будет при сложении давать 34 + 48 + 3 = 85, как в следующем магическом квадрате.

В качестве интересного матемагического пустячка, позвольте мне отметить еще одно удивительное свойство знаменитого магического квадрата 3-на-3 ниже.

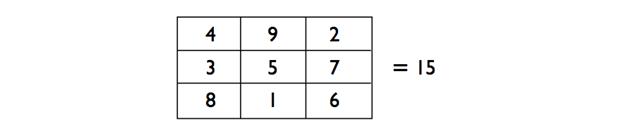
Не только строки, столбцы и диагонали суммируются до 15, но если вы представите строки магического квадрата как трёхзначные числа, то сможете удостовериться на калькуляторе, что 4922 + 3572 + 8162  = 2942  + 7532  + 6182. Также 4382  + 9512  + 2762  = 8342  + 1592  + 6722. Если вам

любопытно,  почему  так  происходит,  вы  возможно  захотите  изучить мою статью «В самом деле «магические» квадраты!»

Быстрые кубические корни

Попросите кого-нибудь выбрать двузначное число и сохранить его в секрете. Затем попросите его возвести число в куб, то есть умножить его само на себя дважды (используя калькулятор). Например, если секретное число 68, пусть доброволец посчитает 68 х 68 х 68 = 314 432. Затем попросите его сказать вам ответ. Как только он назовёт вам куб, 314 432, вы можете мгновенно раскрыть секрет исходного числа - кубический корень, 68. Как?

Чтобы рассчитывать кубические корни, вам нужно выучить кубы чисел от 1 до 10:

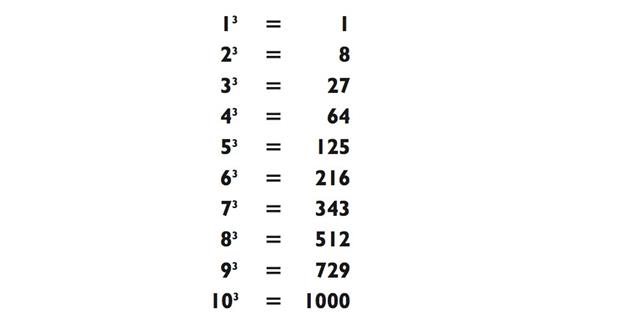
Как только вы выучите эти значения, расчёт кубических корней станет таким же лёгким, как назвать значение числа π . Например, в данном случае: