Определители
Векторное произведение векторов
Векторное произведение векторов, заданных координатами
4. Смешанные произведения векторов
Цели занятия: познакомиться с понятием «матрица», ее математическим и физическим смыслом; понять, что нахождение определителя матрицы является базовым при нахождении векторного и смешанного произведения векторов; понять геометрический смысл смешанного произведения векторов.
Роль и место лекции
Полученные знания будут необходимы для восприятия темы «Матрицы» и «Системы линейных уравнений». Такое фундаментальное понятие, как «определитель» позволит находить решения систем линейных уравнений, смешанное и векторное произведение векторов и т.д. Понятие «смешанное произведение векторов» является одним из связующих звеньев между алгеброй, геометрией и векторным анализом.
1. Определители
Определение 1.
Квадратной матрицей называется таблица чисел, состоящая из n строк и n столбцов. Обозначаются матрицы прописными буквами A , B , C и т. д.
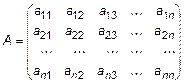 , (1)
, (1)
где 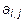 - элемент матрицы, i – номер строки, j – номер столбца.
- элемент матрицы, i – номер строки, j – номер столбца.
Определение 2.
Определителем, или детерминантом второго порядка, называется число, которое можно поставить в соответствие квадратной матрице второго порядка и определяемое следующим образом:
|
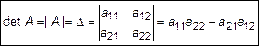 . (2)
. (2)
1.1. Свойства определителя
1. При перестановке 2 строк (столбцов) знак определителя меняется на противоположный:
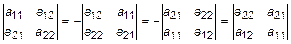 .
.
2. Если все элементы строки, столбца – нули, то определитель равен нулю:
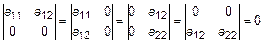 .
.
3. Если в матрице одинаковые две строки (столбца), то определитель равен нулю:
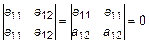 .
.
4. Если в матрице пропорциональны две строки (столбца), то определитель равен нулю:
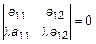 .
.
5. Общий множитель всех элементов строки (столбца) можно выносить за знак определителя:
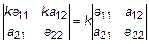 .
.
6. Определитель не изменится, если к элементам одной строки (столбца) матрицы прибавить элементы какой-нибудь другой строки (столбца), умноженные на одно и тоже число:
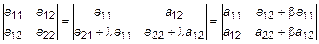 .
.
Доказательство (основано на определении).
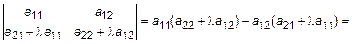
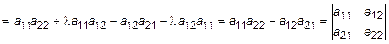 .
.
|
Определителем или детерминантом третьего порядка, называется число, которое можно поставить в соответствие квадратной матрице третьего порядка и определяемое следующим образом:
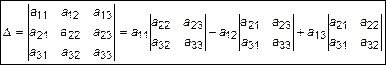 . (3)
. (3)
Замечание !!!
Так как определитель третьего порядка определяется через определитель второго порядка, то все описанные свойства определителя второго порядка справедливы и для третьего.
Определение 4.
Минором 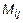 элемента
элемента 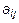 называется определитель , полученный вычеркиванием i -й строки, j -го столбца, на пересечении которых находится элемент:
называется определитель , полученный вычеркиванием i -й строки, j -го столбца, на пересечении которых находится элемент:
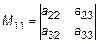 . (4)
. (4)
Учитывая введенное обозначение, запишем определитель третьего порядка:
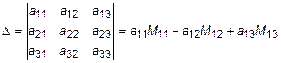 .
.
Определение 5.
Алгебраическим дополнением 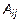 элемента
элемента 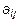 называется минор
называется минор 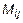 , умноженный на
, умноженный на 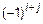 :
: 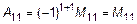 :
:
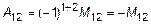 ,
, 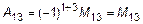 . (5)
. (5)
Учитывая введенное обозначение, запишем определитель третьего порядка:
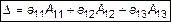 . (6)
. (6)
|
Теорема 1 (Лапласа).
Сумма произведений элементов какой-нибудь строки на их алгебраические дополнения равна определителю. Сумма произведений элементов какой-нибудь строки на алгебраические дополнения другой строки равна нулю:
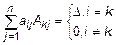 .
.
Определение 6.
Определителем n -го порядка называется число , которое можно поставить в соответствие квадратной матрице n -го порядка и определяемое как
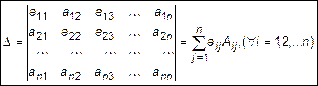 . (7)
. (7)
2. Векторное произведение векторов
Определение 7.
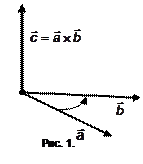 Векторным произведением векторов
Векторным произведением векторов 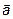 и
и 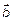 называется вектор
называется вектор 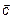 , удовлетворяющий условиям:
, удовлетворяющий условиям:
1) 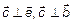 ; 2)
; 2) 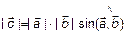 ;
;
3) 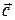 направлен так, что если смотреть из его конца, то кратчайший поворот от первого сомножителя ко второму осуществляется против часовой стрелки (рис. 1), и обозначается
направлен так, что если смотреть из его конца, то кратчайший поворот от первого сомножителя ко второму осуществляется против часовой стрелки (рис. 1), и обозначается 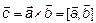 .
.
ПРИМЕР 1.
Вектор угловой скорости 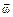 определяется вектором линейной скорости
определяется вектором линейной скорости 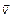 и радиус-вектором
и радиус-вектором 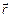 как
как 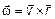 .
.
|
1) 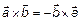 ; 2)
; 2) 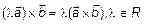 ;
;
3) 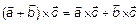 ; 4) Коллинеарности векторов
; 4) Коллинеарности векторов
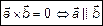 . (8)
. (8)
Дата: 2018-12-21, просмотров: 380.