Условия линейной зависимости векторов
Базис пространств
4. Элементы теории проекций
5. Декартов базис
6. Полярная система координат
Цели занятия: познакомиться с основами векторной алгебры; научиться представлять вектор в декартовом базисе, определять линейную зависимость векторов; познакомиться с основами теории проекций.
Роль и место лекции
Полученные знания будут необходимы для восприятия темы «Векторный анализ, элементы теории поля». Такое фундаментальное понятие, как «базис» позволит взглянуть на понятие размерности пространства с другой стороны и расширить это понятие до n-мерного пространства Понятие линейной независимости необходимо будет при решении систем линейных уравнений и др. Элементы теории проекций особенно необходимы в географических науках, чертежных и др. работах.
1. Линейная зависимость векторов
Пусть задано множество векторов в линейном пространстве L
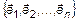(1)
и некоторый ненулевой (если хотя бы одна из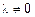 
) набор чисел
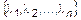. (2)
Определение 1.
Вектор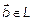 
называется линейной комбинацией векторов системы (1), если он равен сумме попарных произведений векторов системы (1) с соответствующим числом набора (2).
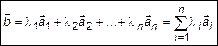(3)
ПРИМЕР 1.
.
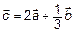Определение 2
|
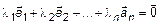. (4)
Если же равенство (4) выполняется только при всех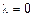 
, то система векторов (1) называется линейно-независимой.
ПРИМЕР 2.
Для векторов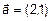 
, 
, 
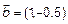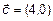запишем: 
, 
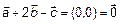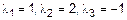, следовательно векторы 
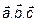- линейно-зависимы.
Замечание !!!
Если среди векторов системы (1) есть хотя бы один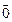 
, система линейно-зависима. Пусть 
, 
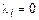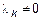для 
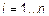и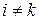 
. Пусть 
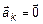по условию. Тогда 
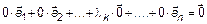, следовательно, система (1) линейно-зависима.
Теорема 1 (критерий линейной зависимости векторов).
Для того чтобы система векторов была линейно-зависима, необходимо и достаточно, чтобы какой-нибудь вектор системы можно было представить в виде линейной комбинации других векторов системы.
Доказательство.
Необходимость. Дана линейно-зависимая система (1). Требуется доказать, что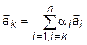 
. Из определения 2 следует, что
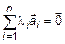(5)
при ненулевом наборе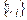 
. Пусть 
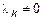. Из (5) можно найти 
:
.
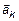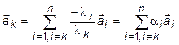Достаточность. Дано
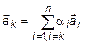. (6)
|
, 
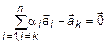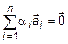, а так как 
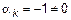, то набор (2) ненулевой, а система (1) линейно-зависима.
Следствие!!!
Два вектора линейно зависимы тогда и только тогда, когда они коллинеарные, т. е.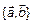 
– линейно-зависимы 
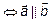, т. к. по условию коллинеарности следует, что 
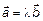, откуда по теореме 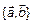– линейно-зависимы.
2. Условия линейной зависимости векторов
Теорема 2.
Три вектора линейно-зависимы тогда и только тогда, когда они компланарны, т. е.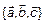 
– линейно-зависимы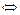 
.
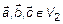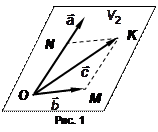Доказательство.
Необходимость. Дано 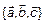– линейно-зависимы. Доказать: 
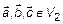. Из теоремы 1 следует, что 
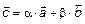, где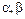 
– числа. По определению 
, 
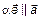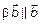, следовательно, 
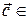пл. (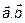 
), 
.
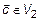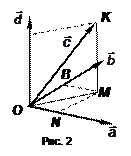Достаточность. Дано: 
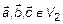. Доказать, что 
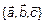– линейно-зависимы. Представим три вектора в одной плоскости (рис.1). На основаниях векторов 
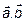построим параллелограмм так, чтобы вектор 
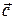был диагональю этого параллелограмма ONKM. Тогда 
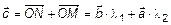, следовательно, по теореме 1 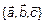– линейно-зависимы.
Теорема 3
Любые четыре вектора в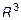 
линейно-зависимы.
Доказательство.
Изобразим произвольно 4 вектора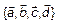 
в пространстве. По рис. 2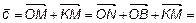 
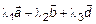. Следовательно, по теореме 1, 
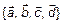– линейно-зависимы.
3. Базис пространств
Дана система векторов в L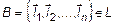 
. (7)
Определение 3.
|
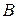– полная, если 
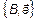– линейно-зависимы, 
, 
.
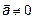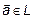Определение 4.
Полная, линейно независимая система векторов в пространстве называется базисом этого пространства.
ПРИМЕР 3.
Есл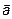и 
и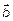 
не коллинеарные, то в 
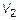они образуют базис. По определению они линейно-независимые. Это полная система потому, что присоединение 3-го вектора приведет к образованию трех компланарных векторов в 
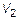, а следовательно, согласно теореме 2 они линейно-зависимы.
Следствие !!!
Из теоремы 1 и определения 4 следует, что любой вектор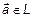 
можно представить в виде линейной комбинации базисных векторов:
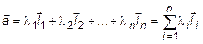. (8)
Выражение (8) называется разложением вектора в данном базисе, а числа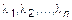 
– координатами 
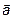в базисе B: 
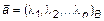. В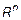 
чаще всего принимают базис, векторы которого ортогональны.
, 
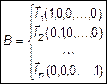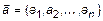. (9)
Теорема 4 (единственности разложения вектора в базисе).
Разложение вектора в данном базисе единственно.
Доказательство (от противного).
Предположим, что верно (8) и верно
|
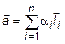, (10)
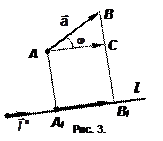где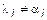 
хотя бы для одного i. Вычтем из (8) равенство (10) 
- 
= 
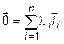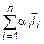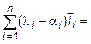
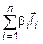. Следовательно, система B линейно-зависима, а это противоречит тому, что система B – базис. Предположение не верно, т. е. 
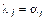для любых i, значит, разложение единственное.
Определение 5.
Число векторов базиса называется размерностью пространства.
Следствие!!!
Из теоремы 2 следует, что 3 некомпланарных вектора образуют базис (трехмерное пространство).
4. Элементы теории проекций
Определение 6.
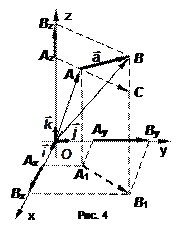Проекцией вектора 
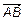на ось l ,если он сонаправлен с вектором 
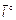, называется число, равное длине вектора 
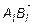, и противоположное число, если направление противоположно 
( 
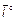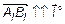, если 
, и -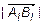 
, если 
).
= 
,
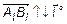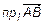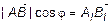где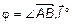 
.
Теорема 5.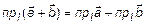 
.
Теорема 6.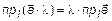 
.
5. Декартов базис
В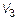 
за базис примем 
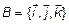, где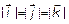 
; 
, 
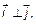
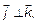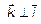– декартов базис. Тогда любой вектор 
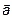можно разложить в этом базисе (рис. 4).
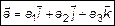, (11)
где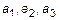 
– координаты 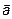в базисе.
Теорема 7.
|
Из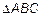 
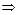
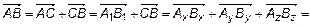
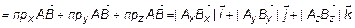. (12)
Согласно теореме 4 данное разложение (12) единственное. Из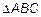 
по определению нормы в 
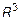следует, что 
, 
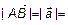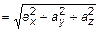, где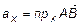 
, 
, 
.
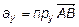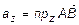Определение 7.
Радиус-вектором точки называется вектор, соединяющий начало координат с этой точкой. Обозначается для точки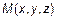 
как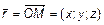 
; 
.
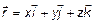Пусть даны точк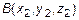и 
и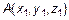 
. Их соответствующие радиус-векторы равны 
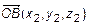и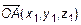 
(рис. 4). Из 
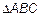получим 
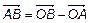. Для проекции на Ox имеем
.
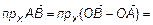
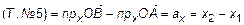Аналогичные рассуждения можно провести для остальных проекций. Тогда получим:
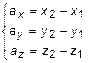(13)
Теорема 8.
Координаты вектора равны разности координат конца и начала вектор:
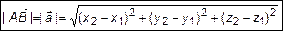. (14)
6. Полярная система координат
В полярной системе координат вектор задается следующим образом. Задается его длина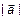 
и угол 
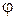поворота, отложенный от положительного направления оси 
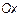. Положительный угол считается при повороте против часовой стрелки. Задать вектор в полярных координатах означает задать его норму и угол (рис. 5). То есть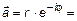 
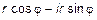– формула Эйлера, где i = 
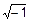– мнимая единица. Данные вопросы относятся к теории комплексных чисел и будут изучаться позже. В соответствии с рис. 5 можно привести формулы, связывающие декартову и полярные системы координат: 
, 
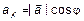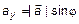. Окончательно получим
|
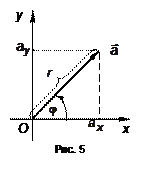
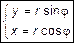. (15)
Заключение
В лекции векторная алгебра освящена на более высоком уровне. Декартова система координат представлена на основе теории проекций. Это дает более глубокое понимание вектора в трехмерном пространстве. Введено фундаментальное понятие «базис». Отметим следующее:
- размерность пространства определяется его базисом;
- линейная зависимость означает возможность представить один вектор в виде линейной комбинации других векторов;
- базис может быть и не ортогональным;
- разложение в данном базисе единственное;
- существуют другие системы координат.
Литература
1. Бермант А.Ф. и др. Краткий курс математического анализа. – М.: Высшая школа, 2001.
2. Рыжков В. В. Лекции по аналитической геометрии. – М.: Факториал пресс, 2000, – 208 с.
3. Шнейдер В.Е. и др. Краткий курс высшей математики. – М.: Высшая школа, 1998.
4. Ефимов Н.В. Краткий курс аналитической геометрии. – М.: Физматлит, 2002.
5. Шипачев В.С. Основы высшей математики. - М.: Высшая школа,1998.
6. Кудрявцев В.А., Демидович Б.П. Краткий курс высшей математики. – М.: Наука, 1989, – 659 с.
7. Фихтенгольц Г.М. Основы математического анализа. Часть 1. – М.: Лань, 2002, – 440 с.
Лекция 7
Эвклидово пространство
|
Дата: 2018-12-21, просмотров: 268.
