Уравнение поверхности
Уравнение плоскости, проходящей через заданную точку
Общее уравнение плоскости и его исследование
4. Уравнение плоскости в отрезках
5. Уравнение плоскости, проходящей через три заданные точки
6. Угол между двумя плоскостями
7. Расстояние от точки до плоскости
|
Роль и место лекции
В предыдущей лекции закончена тема «Матрицы и системы линейных уравнений». Лекцией 11 открывается тема «Аналитическая геометрия». Ее цель – научиться получать аналитические зависимости между координатами точек пространства. Однако знания, полученные по теории матриц, необходимы и в этой теме, например представление плоскости, проходящей через три заданные точки. Знания, полученные по системам линейных уравнений, необходимы при решении вопроса о пересечении плоскостей и. т.д. В данной теме пригодятся знания и векторной алгебры.
1. Уравнение поверхности
Определение 1.
Поверхность – это совокупность точек, обладающих общим свойством.
Математически это общее свойство выражается уравнением, связывающим координаты точек поверхности. В 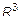 уравнение поверхности задается в общем виде:
уравнение поверхности задается в общем виде: 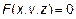 .
.
Определение 2.
Уравнение поверхности в 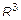 называется уравнение с тремя переменными, которому удовлетворяет любая точка этой поверхности и не удовлетворяет точка, не принадлежащая ей.
называется уравнение с тремя переменными, которому удовлетворяет любая точка этой поверхности и не удовлетворяет точка, не принадлежащая ей.
ПРИМЕР 1.
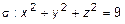 – сферическая поверхность. Точка
– сферическая поверхность. Точка 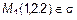 , а
, а 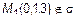 .
.
2. Уравнение плоскости, проходящей через заданную точку.
|
 . Возьмем любую точку
. Возьмем любую точку 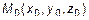 в
в 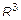 и вектор
и вектор 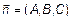 :
: 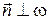 (рис. 1). Возьмем любую точка пространства
(рис. 1). Возьмем любую точка пространства 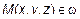 , где
, где 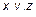 – текущие координаты. Рассмотрим векторы
– текущие координаты. Рассмотрим векторы 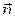 и
и 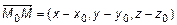 . По условию
. По условию 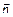
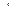
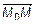 . Следовательно, их скалярное произведение равно 0. Запишем общее свойство точек плоскости:
. Следовательно, их скалярное произведение равно 0. Запишем общее свойство точек плоскости:
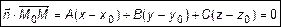 . (1)
. (1)
 Уравнение (1) есть уравнение плоскости
Уравнение (1) есть уравнение плоскости 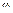 , проходящей через заданную точку
, проходящей через заданную точку 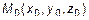 и перпендикулярной вектору нормали
и перпендикулярной вектору нормали 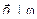 (рис. 1). С учетом того, что вектор
(рис. 1). С учетом того, что вектор 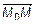 определяется разностью радиус-векторов
определяется разностью радиус-векторов 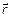 и
и 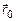 соответственно
соответственно 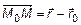 , выражение (1) можно записать в векторной форме
, выражение (1) можно записать в векторной форме
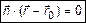 . (2)
. (2)
Вывод !!!
Любая плоскость описывается уравнением первого порядка.
3. Общее уравнение плоскости и его исследование
Возьмем общее уравнение первого порядка и докажем, что ему соответствует плоскость. Для этого приведем его к виду (1). Общее уравнение первого порядка
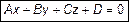 . (3)
. (3)
|
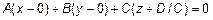 .
.
Сравним с (1) и сделаем вывод, что это уравнение плоскости, проходящей через точку 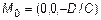 и
и 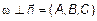 . Уравнение (3) называется общим уравнением плоскости. Плоскость – это поверхность первого порядка. В зависимости от значений A, B, C и D плоскость занимает определенное положение относительно системы координат. Рассмотрим эти случаи.
. Уравнение (3) называется общим уравнением плоскости. Плоскость – это поверхность первого порядка. В зависимости от значений A, B, C и D плоскость занимает определенное положение относительно системы координат. Рассмотрим эти случаи.
I. Одна из констант A, B, C равна нулю.
1) Пусть A =0. Тогда 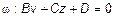 . Вектор
. Вектор 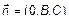 ,
, 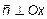
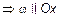 (рис. 2).
(рис. 2).
2) Пусть B =0. Тогда 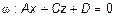 . Вектор
. Вектор 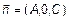 ,
, 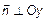
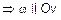 (рис. 3).
(рис. 3).
3) Пусть C =0. Тогда 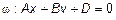 . Вектор
. Вектор 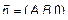 ,
, 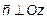
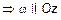 (рис. 4).
(рис. 4).

Вывод !!!
Если в общем уравнении плоскости отсутствует одна из переменных, то плоскость параллельна координатной оси, одноименной с отсутствующей переменной.
II. Свободный коэффициент D=0. Следовательно, точка 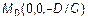 или
или 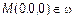 . Плоскость проходит через начало координат.
. Плоскость проходит через начало координат.
Вывод !!!
Если в общем уравнении плоскости отсутствует свободный коэффициент, то плоскость проходит через начало координат.
III. Одна из констант A, B, C равна нулю и D=0.
1) Пусть A =0. Тогда 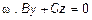 ,
, 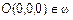 и
и 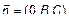 ,
, 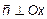
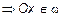 (рис. 5).
(рис. 5).
|
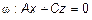 ,
, 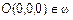 и
и 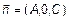 ,
, 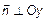
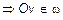 (рис. 6).
(рис. 6).
3) Пусть C =0. Тогда 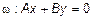 ,
, 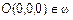 и
и 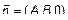 ,
, 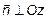
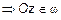 (рис. 7).
(рис. 7).

Вывод !!!
Если в общем уравнении плоскости отсутствует одна из переменных и свободный коэффициент, то плоскости принадлежит координатная ось, одноименная с отсутствующей переменной.
IV. Две из констант равна нулю:
1) Пусть A=B=0. Тогда 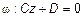 , или
, или 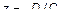
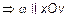 (рис. 8).
(рис. 8).
2) Пусть A=C=0. Тогда 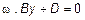 , или
, или 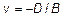
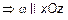 (рис. 9).
(рис. 9).
3) Пусть B=C=0. Тогда 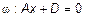 , или
, или 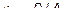
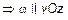 (рис. 10).
(рис. 10).

Вывод !!!
Если в общем уравнении плоскости отсутствует две из переменных, то плоскость параллельна координатной плоскости, одноименной с отсутствующими переменными.
|
1) Пусть A=B = D=0. Тогда 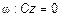 , или
, или 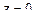
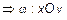 (рис. 11).
(рис. 11).
2) Пусть A=C = D=0. Тогда 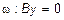 , или
, или 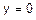
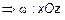 (рис. 12).
(рис. 12).
3) Пусть B=C = D=0. Тогда 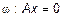 , или
, или 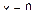
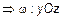 (рис. 13).
(рис. 13).

Вывод !!!
Если в общем уравнении плоскости две из переменных и свободный член отсутствуют, то плоскость есть координатная плоскость, одноименная отсутствующим переменным.
4. Уравнение плоскости в отрезках.
Возьмем общее уравнение плоскости (3). Обозначим точки пересечения плоскости с координатными осями как:
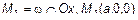 ,
, 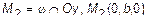 ,
, 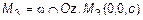 .
.
Поскольку эти точки принадлежат плоскости, то они должны удовлетворять (3). Подставим значение координат точек в (3) и получим
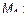
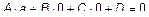
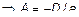 ;
;
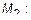
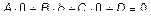
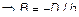 ;
;
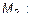
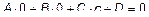
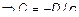 .
.
Подставим эти значения в (3)
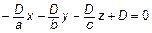 или
или 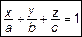 . (4)
. (4)
Выражение (4) есть уравнение плоскости в отрезках.
ПРИМЕР 2.
Построить плоскость, заданную уравнением 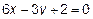 . Приведем это выражение к виду (3)
. Приведем это выражение к виду (3)
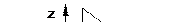
|
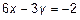

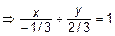 . То есть
. То есть 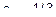 ,
, 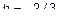 . Это плоскость параллельная оси
. Это плоскость параллельная оси 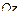 . Действительно
. Действительно 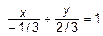 можно представить как
можно представить как 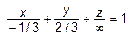 , где
, где 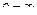 – бесконечно большая величина. То есть ось
– бесконечно большая величина. То есть ось 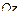 не пересекается плоскостью. Плоскость представлена на рис. 14.
не пересекается плоскостью. Плоскость представлена на рис. 14.
5. Уравнение плоскости,
проходящей через три заданные точки
 Даны три точки плоскости
Даны три точки плоскости 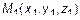 ,
, 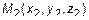 ,
, 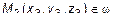 . Тогда для любой
. Тогда для любой 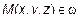 можно построить три вектора
можно построить три вектора 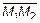 ,
, 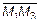 ,
, 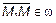 (рис. 15). По условию они лежат в одной плоскости, или компланарны, поэтому их смешанное произведение равно нулю. Получим уравнение плоскости
(рис. 15). По условию они лежат в одной плоскости, или компланарны, поэтому их смешанное произведение равно нулю. Получим уравнение плоскости
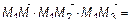
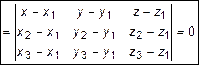 . (5)
. (5)
6. Угол между двумя плоскостями
Пусть в 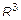 заданы две плоскости
заданы две плоскости 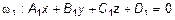 и
и 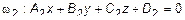 . Обозначим угол между плоскостями как
. Обозначим угол между плоскостями как 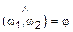 . Очевидно, что этот угол
. Очевидно, что этот угол 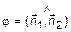 , где
, где 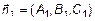 и
и 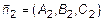 . Тогда
. Тогда
|
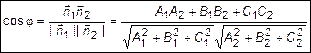 . (6)
. (6)
6.1. Условие перпендикулярности плоскостей
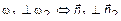 или
или 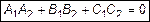 .
.
6.2. Условие параллельности плоскостей
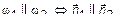 или
или 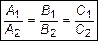 .
.
ПРИМЕР 3.
Дано: 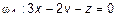 ,
, 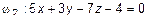 ,
,
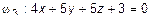 ,
, 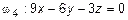 .
.
Расположение плоскостей: 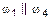 ,
, 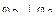 .
.
7. Расстояние от точки до плоскости
 Пусть задана точка
Пусть задана точка 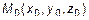 и плоскость
и плоскость 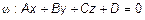 . Возьмем произвольную точку
. Возьмем произвольную точку 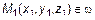 . Очевидно (рис. 16), что расстояние от точки
. Очевидно (рис. 16), что расстояние от точки 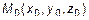 до плоскости
до плоскости 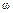 определяется проекцией вектора
определяется проекцией вектора 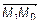 на вектор нормали
на вектор нормали 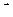 . Следовательно,
. Следовательно,
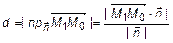
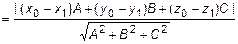
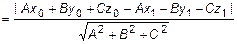
Так как точка 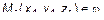 , то
, то 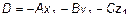 . Подставим это значение и получим
. Подставим это значение и получим
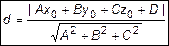 . (7)
. (7)
Заключение
|
Отметим следующее:
- вид поверхности определяется видом уравнения и типом пространства;
- уравнения плоскости получаются на основе свойств векторов;
- плоскость в 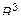 описывается общим уравнением первого порядка;
описывается общим уравнением первого порядка;
- вектор нормали к плоскости определяется координатами 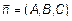 ;
;
- угол между плоскостями определяется на основе скалярного произведения векторов нормалей к плоскостям;
- расстояние от точки до плоскости определяется на основе свойств проекций.
Литература
1. Рыжков В.В. Лекции по аналитической геометрии. - М.: Факториал пресс, 2000. -208 с.
2. Ефимов Н.В. Краткий курс аналитической геометрии. – М.: Физматлит, 2002.
3. Шипачев В.С. Основы высшей математики. - М.: Высшая школа,1998.
4. Кудрявцев В.А., Демидович Б.П. Краткий курс высшей математики. – М.: Наука, 1989, - 659 с.
5. Баврин И.И. Высшая математика. – М.: Просвещение, 1980.
Лекция 12
85
Прямая линия в пространстве
Дата: 2018-12-21, просмотров: 389.