Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Предмет и методы аналитической геометрии

Линейные пространства

Нормированные пространства

4. Векторы в пространстве

5. Линейные операции над векторами

Цели занятия: определить роль математики в конкретной специальности, ее важность и необходимость; познакомиться с основными понятиями, методами и приемами высшей математики.

Роль и место лекции

Последующее знакомство с математикой будет базироваться на тех понятиях дискретной математики, которые изучены в первых четырех лекциях.

Обратимся теперь к окружающему нас миру как к миру, поддающемуся математическому описанию. Очевидно, первое, с чего надо начать – это с того, с чего начинали древние математики: понятия «геометрия» и «пространство».

1. Предмет и методы аналитической геометрии

Для успешных запусков космических аппаратов необходим точный расчет траекторий полета. Конструирование мостов и других сооружений происходит в строгом соответствии с результатами расчета геометрических параметров. В программировании для визуализации объектов необходимы знания для расчетов формы и траектории движения отдельных полигонов. В экономических задачах исследуют динамику и поведение рынка по графическим зависимостям и т.д.

Предметом аналитической геометрии является исследование форм геометрических образов и их взаиморасположение с помощью алгебры и анализа. Основные методы:

1. Метод координат; 2. Метод линейной геометрии.

Метод координат состоит в том, чтобы определить положение одного геометрического образа относительно другого с помощью чисел. С помощью метода координат каждой линии можно

37

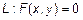поставить в соответствие уравнение . В аналитической геометрии на плоскости рассматриваются линии, описанные алгебраическими уравнениями 1-го порядка (прямая 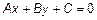) и алгебраическими уравнениями 2-го порядка (эллипс, окружность, гипербола, парабола 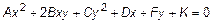). С помощью метода координат каждой поверхности в пространстве можно поставить в соответствие уравнение .

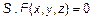Основные задачи аналитической геометрии

1. Дан геометрический образ (l или S) – составить уравнение.

2. По известному уравнению геометрического образа составить его вид.

  2. Линейные пространства

Определение  1.

Числовым полем называется любое числовое множество, замкнутое относительно операций сложения, вычитания, умножения и деления (кроме деления на 0). Аналогичное определение можно дать для различных полей.

Определение  2.

Непустое множество элементов любой природы называется линейным пространством ( L ) на некотором поле, если оно удовлетворяет двум условиям

I . 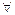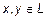, 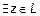: 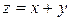. Определена операция сложения, не выводящая за пределы L и обладающая определенными свойствами:

1) 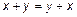– свойство коммутативности (перестановки);

2) 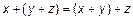 – свойство ассоциативности;

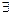
3) 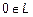: 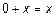– существование нулевого элемента;

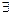
4) 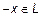:  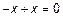– существование отрицательных элементов.

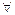
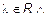
II . 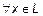, 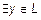: 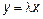. Возможна операция умножения на число, обладающая определенными свойствами:

1) , ;

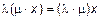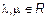2) 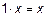– существование единичного элемента;

3) 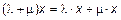 – дистрибутивное свойство;

4)  – дистрибутивное свойство.

ПРИМЕР 1. Линейные пространства.

1. R – множество действительных чисел.

2. 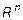 – n-мерное пр-во, множество упорядоченных наборов действительных чисел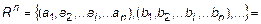 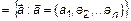. В частности,  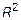– множество точек плоскости,  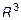– множество точек пространства.

3. 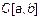 – множество функций, непрерывных на 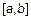. В частности,  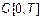– пространство непрерывных сигналов ( ).

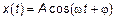4. 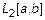 – множество функций квадратинтегрируемых на 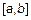, т. е. существует .

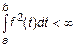3. Нормированные пространства

Определение  3.

Отображение линейного пространства L на множество действительных чисел R называется функционалом .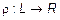

Определение  4.

Нормой элемента 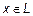 называется функционал 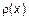, удовлетворяющий условиям:

1) ;

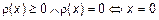2) ;

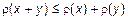3) .

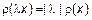Норма элемента x обозначается значком || x ||. Пространство, в котором введена норма, называется нормированным .

ПРИМЕР 2.

1. Для R, .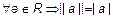

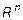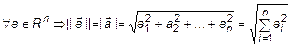38

2. Для , .

3. Для 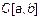 за норму принимают .

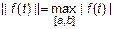4. Для , норма ,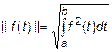

 

4. Векторы в пространстве

39

Скалярная величина – это численное значение.

Векторная величина определена не только численным значением, но и направлением.

Определение 5.

Вектором называется направленный отрезок прямой и обозначается 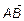  или 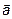, где A – начало вектора; В – конец вектора. 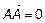; модуль вектора  – , , .

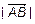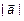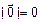Определение 6.

Два вектора называются коллинеарными, если они лежат на одной или на параллельных прямых, обозначаются 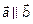. Если  они направлены в одну сторону (сонаправленные), то записывают 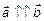, а если в противоположные, то записывают .

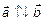Определение 7.

Два вектора равны 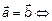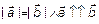, два вектора противоположны .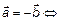

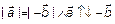Определение 8.

Если векторы лежат на одной или параллельных плоскостях, то они называются компланарными (соплоскостными).

5. Линейные операции над векторами

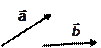5.1. Сложение векторов

Дано: 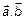. Найти: .              

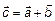1. Правило треугольника (рис. 1а).

2. Правило параллелограмма (рис. 1в).

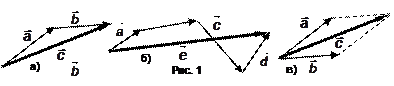
Если слагаемых векторов больше 2, правило треугольника обобщается правилом многоугольника (рис. 1б) .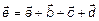

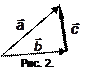5.2. Вычитание векторов

Т. к. 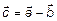,  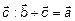или 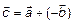. Следовательно, справедливо правило параллелограмма или треугольника. Вектор  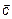имеет следующее направление: начало вектора совпадает с концом вычитаемого вектора, и конец вектора совпадает с началом вектора, из которого вычитают (рис. 2).

5.3. Умножение вектора на скаляр

Определение 9.

40

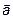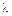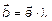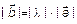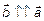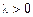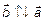Произведение вектора  на скаляр  называется вектор . Следствия: a ) ; б)  если ,  если 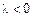; в) Если 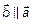, то .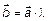

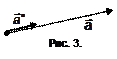Определение 10.

Вектор 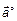 называется единичным вектором (рис. 3) вектора 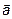, если ,  

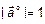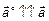
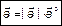
Заключение

В лекции определены роль и место высшей математики в современной науке; изучены предмет, методы и задачи аналитической геометрии, понятия линейного, нормированного пространств. Они важны для восприятия в дальнейшем известных со школы понятий и операций с точки зрения высшей математики. Обращалось внимание на часть школьного курса о векторах и операциях над ними, чтобы в дальнейшем систематизировать знания по векторной алгебре. Отметим следующее:

- математика – точный инструмент всех наук;

- линии описываются алгебраическими уравнениями 1-го порядка (прямая) и алгебраическими уравнениями 2-го порядка (эллипс, окружность, гипербола, парабола);

- норма в 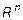 пространстве задается как длина вектора;

-  существуют линейные пространства, они могут быть нормированными.

Литература

1. Бермант А.Ф. и др. Краткий курс математического анализа. – М.: Высшая школа, 2001.

2. Рыжков В. В. Лекции по аналитической геометрии. – М.: Факториал пресс, 2000, – 208 с.

3. Шнейдер В.Е. и др. Краткий курс высшей математики. – М.: Высшая школа, 1998.

4. Ефимов Н.В. Краткий курс аналитической геометрии. – М.: Физматлит, 2002.

41

Лекция 6

Элементы векторной алгебры