Суперпозиция бинарных отношений
Свойства суперпозиций бинарных отношений
Цели занятия: изучить понятие отношения на множестве как его некоторые подмножества; научиться осуществлять операции над отношениями; понять принцип суперпозиции отношений.
Роль и место лекции
На предыдущих лекциях мы познакомились с основными терминами и операциями над множествами. Из школьного курса математики известно понятие функции, как некоторой зависимости между действительными элементами области определения и действительными значениями области значений. В этой лекции станет понятным, что это лишь частный случай. Понятие функции более широкое.
Кроме того, в последующих лекциях по линейной алгебре и теории аналитических функций будут рассматриваться с точки зрения множеств такие важные понятия как «оператор» и «функционал». Следует обратить внимание на понятия «суперпозиция» и «обратное отношение», которые непосредственно связаны с уже известными вам понятиями сложной и обратной функции действительного переменного. Именно знания по дискретной математике позволяют понимать и «чувствовать» математику на более высоком уровне.
1. Отношения на множествах
Определение 1.
Отношение – это один из способов задания взаимосвязей между элементами множеств. Они бывают унарные, бинарные и в общем случае n -арные.
Определение 2.
Унарные (одноместные) отношения на множестве – это наличие какого-то определенного признака R (свойства и т. п.) у элементов a некоторого множества M . Унарное отношение образует некоторое подмножество на множестве, в котором они введены, т. е. 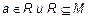 .
.
|
Множество животных одного вида являются подмножеством множества рода животных и т. д. Так {грызуны} 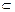 {млекопитающие} подмножество задано отношением «класс»
{млекопитающие} подмножество задано отношением «класс»
Определение 3.
Соответствие – это способ задания взаимосвязей, взаимодействий между элементами множества (наряду с отношениями). Частными случаями соответствия являются функции, операции, преобразования и др.
Определение 4.
Два множества называются эквивалентными, если для любого элемента а множества А найдется такой элемент b множества В, что 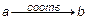 .
.
2. Бинарные отношения
Определение 5.
Бинарное (двухместное) отношение на множестве – это наличие каких-либо взаимосвязей R , которыми характеризуются пары элементов на некотором множестве M . Тогда все пары 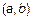 элементов из М, между которыми имеет место данное отношение R ,образуют подмножество пар из множества всех возможных пар элементов
элементов из М, между которыми имеет место данное отношение R ,образуют подмножество пар из множества всех возможных пар элементов 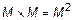 , т. е.
, т. е. 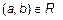 , при этом
, при этом 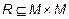 .
.
Определение 6.
Сокращенное определение. Говорят, что на множестве M задано бинарное отношение 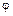 , если в M×M выделено некоторое подмножество
, если в M×M выделено некоторое подмножество 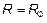 .
.
Другими словами, бинарное отношение на множестве M – это подмножество в M×M. Утверждение, что элемент a состоит в отношении 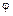 с элементом b, означает, что пара
с элементом b, означает, что пара 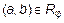 , или
, или
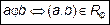 . (1)
. (1)
ПРИМЕР 2.
1. Отношение делимости в N. Число n состоит в этом отношении с числом m, если n делится на m {(1,1),(3,6),(3,9)…}:. Подмножество R в N2, определяющее отношение делимости, имеет вид: R = {(n,m) 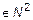 :
: 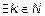 : n = km}.
: n = km}.
2. Отношение " 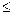 " в R. Число x состоит в этом отношении с числом y, если x
" в R. Число x состоит в этом отношении с числом y, если x 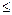 y {(1,2); (3,3); (2,12)…}. Соответствующее подмножество в R2 определяется следующим образом: R = {(x,y)
y {(1,2); (3,3); (2,12)…}. Соответствующее подмножество в R2 определяется следующим образом: R = {(x,y) 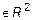 : x
: x 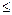 y}.
y}.
3. Отношение равенства в R. Числа x и y состоят в этом отношении, если они равны {(1,1),(3,3)…}: R = {(x,y) 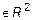 : x=y}.
: x=y}.
4. Отношение {семейной пары} на множестве {люди}.
Определение 7.
Бинарное отношение 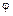 , заданное на множестве M называется:
, заданное на множестве M называется:
- рефлексивным, если a 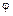 a для
a для 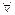 a
a 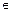 M,
M,
- симметричным, если a 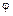 b
b 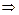 b
b 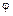 a,
a,
- антисимметричным, если (a 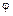 b) и (b
b) и (b 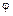 a)
a) 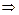 a = b,
a = b,
- транзитивным, если (a 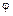 b) и (b
b) и (b 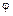 с)
с) 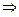 a
a 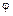 c.
c.
ПРИМЕР 3.
|
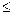 ", заданное на множестве R, является рефлексивным, однако отношение "<", заданное на том же самом множестве R, не рефлексивно. Докажем второе утверждение. Бинарное отношение " < " это:
", заданное на множестве R, является рефлексивным, однако отношение "<", заданное на том же самом множестве R, не рефлексивно. Докажем второе утверждение. Бинарное отношение " < " это:
"<"=R = {(x,y) 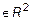 : x<y},
: x<y},
означающее, что произвольный элемент 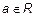 должен удовлетворять неравенству a < a, а это неправда. Следовательно, произвольный элемент a не состоит сам с собой в отношении "<", и рефлексивности нет. Множество {животные одного вида} рефлексивно.
должен удовлетворять неравенству a < a, а это неправда. Следовательно, произвольный элемент a не состоит сам с собой в отношении "<", и рефлексивности нет. Множество {животные одного вида} рефлексивно.
2. Определим на множестве R следующее бинарное отношение: элементы 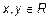 связаны бинарным отношением
связаны бинарным отношением 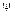 , если равны их целые части [x]=[y]. Докажем, что определенное таким образом бинарное отношение
, если равны их целые части [x]=[y]. Докажем, что определенное таким образом бинарное отношение 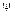 обладает свойством симметричности. Действительно, имеет место следующее соотношение
обладает свойством симметричности. Действительно, имеет место следующее соотношение
[x] = [y] 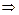 [y] = [x].
[y] = [x].
Определение 8.
Бинарное отношение 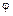 , заданное на множестве M, называется отношением эквивалентности, если оно рефлексивно, симметрично и транзитивно (см. определение 4).
, заданное на множестве M, называется отношением эквивалентности, если оно рефлексивно, симметрично и транзитивно (см. определение 4).
|
Пусть на множестве M={1, 2, 3} задано бинарное отношение 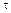 ={(1,2); (2,1); (1,1); (2,2); (3,3)}. Доказать, что заданное таким образом бинарное отношение
={(1,2); (2,1); (1,1); (2,2); (3,3)}. Доказать, что заданное таким образом бинарное отношение 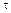 является отношением эквивалентности. Нужно показать, что бинарное отношение
является отношением эквивалентности. Нужно показать, что бинарное отношение 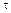 обладает свойствами рефлексивности, симметричности и транзитивности.
обладает свойствами рефлексивности, симметричности и транзитивности.
1. Необходимо проверить, что для любого элемента a из множества M пара (a,a) принадлежит бинарному отношению 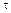 . Здесь a = 1, 2, 3 и из определения
. Здесь a = 1, 2, 3 и из определения 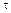 видно, что пары (1,1), (2,2), (3,3) принадлежат бинарному отношению
видно, что пары (1,1), (2,2), (3,3) принадлежат бинарному отношению 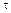 .
.
2. Выполнение условия 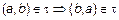 видно прямо из определения бинарного отношения
видно прямо из определения бинарного отношения 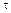 .
.
3. Должно выполняться свойство: 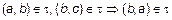 .
.
Действительно: 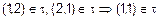 ,
, 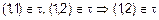 и т. д.
и т. д.
3. Операции над бинарными отношениями
Мы уже знаем, что бинарные отношения являются множествами, и, следовательно, можно говорить о равенстве бинарных отношений и о включении одного бинарного отношения в другое: 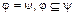 . На бинарные отношения, заданные на некотором множестве переносятся общие операции над множествами. Пусть
. На бинарные отношения, заданные на некотором множестве переносятся общие операции над множествами. Пусть 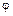 и
и 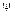 – бинарные отношения, заданные на множестве A. Тогда:
– бинарные отношения, заданные на множестве A. Тогда:
- 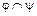 – бинарное отношение в A, пересечение отношений
– бинарное отношение в A, пересечение отношений 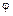 и
и 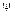 ;
;
- 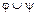 – бинарное отношение в A, объединение отношений
– бинарное отношение в A, объединение отношений 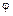 и
и 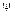 ;
;
- 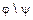 – бинарное отношение в A, разность отношений
– бинарное отношение в A, разность отношений 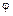 и
и 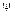 ;
;
- 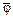 – бинарное отношение в A, дополнение к бинарному отношению
– бинарное отношение в A, дополнение к бинарному отношению 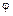 в A, т. е.
в A, т. е. 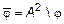 .
.
ПРИМЕР 5.
Определим следующие бинарные отношения:
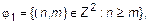
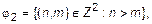
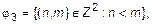

тогда между ними имеют место следующие отношения включения: 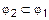 ;
; 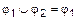 ;
; 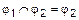 ;
; 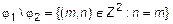 . Последнее бинарное отношение является отношением равенства в Z и т.д.
. Последнее бинарное отношение является отношением равенства в Z и т.д.
В биологии отношение на множестве {ареал} может определять подмножество {вид животных}.
4. Суперпозиция бинарных отношений
Определение 9.
|
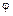 и
и 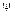 называется бинарное отношение (будем обозначать его как
называется бинарное отношение (будем обозначать его как 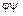 ), определенное следующим образом:
), определенное следующим образом: 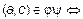 когда в множестве A найдется хотя бы один элемент b, такой, что
когда в множестве A найдется хотя бы один элемент b, такой, что 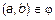 и
и 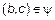 .
.
Определение 10.
Множество называется связным, если на этом множестве можно определить суперпозицию любых подмножеств.
ПРИМЕР 6.
Для бинарных отношений, определенных в предыдущем примере, нужно показать, что справедливы следующие равенства:
1. 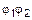 =
= 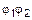 =
= 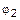 . Действительно, поскольку
. Действительно, поскольку 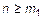 ,
, 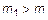 , то
, то 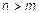 ; обратно, если
; обратно, если 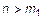 ,
, 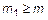 , то
, то 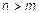 ;
;
2. 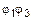 =
= 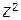 . Рассмотрим произвольную пару
. Рассмотрим произвольную пару 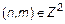 , возможны два случая a)
, возможны два случая a) 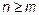 ; b)
; b) 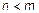 . Рассмотрим случай a)
. Рассмотрим случай a) 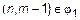 ,
, 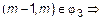
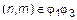 . В случае b)
. В случае b) 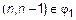 ,
, 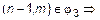
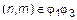 . Итак, мы показали, что
. Итак, мы показали, что 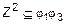 и, следовательно,
и, следовательно, 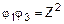 ;
;
3. 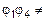
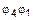 .
.
Замечание!!!
Этот пример показывает, что суперпозиция бинарных отношений, вообще говоря, не обладает свойством коммутативности.
Доказательство.
Поскольку 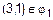 и
и 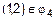 , получаем, что пара
, получаем, что пара 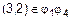 . Теперь надо показать, что пара
. Теперь надо показать, что пара 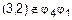 . Перепишем бинарное отношение
. Перепишем бинарное отношение 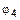 как
как 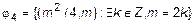 . Следовательно,
. Следовательно, 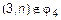 , причем для любого n, откуда получаем, что пара
, причем для любого n, откуда получаем, что пара 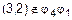 , ибо в противном случае
, ибо в противном случае 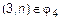 , что невозможно. Однако легко показать, что
, что невозможно. Однако легко показать, что
|
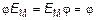 ;
; 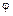
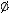 =
= 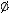
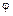 =
= 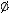 .
.
Здесь EM – бинарное отношение равенства в множестве M.
5. Свойства суперпозиций бинарных отношений
1. Свойство объединения. Пусть во множестве A заданы бинарные отношения 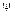 и
и 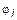 ,
, 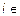 I. Здесь I - конечный или бесконечный набор индексов. Тогда
I. Здесь I - конечный или бесконечный набор индексов. Тогда
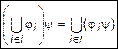 ,
, 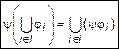 . (2)
. (2)
Заметим, что в вышеприведенных соотношениях значки 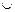 нельзя заменить на
нельзя заменить на 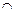 .
.
Доказательство.
Пусть 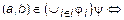
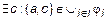 и
и 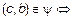
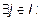
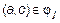
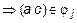
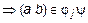
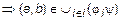 .
.
2. Свойство ассоциативности. Для любых бинарных отношений 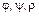 , заданных на некотором множестве A, справедливо равенство:
, заданных на некотором множестве A, справедливо равенство:
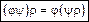 . (3)
. (3)
Доказательство.
Пусть пара 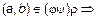
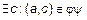 и
и 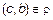 . Это означает, что
. Это означает, что 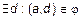 и
и 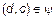
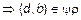 и
и 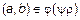 . Итак, мы доказали, что если
. Итак, мы доказали, что если 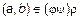 , то из этого следует, что
, то из этого следует, что 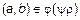 . Обратное включение доказывается аналогично.
. Обратное включение доказывается аналогично.
Это утверждение говорит о том, что какими бы двумя различными способами ни расставлять скобки в выражении 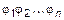 , чтобы получить суперпозицию двух отношений, получим равные отношения.
, чтобы получить суперпозицию двух отношений, получим равные отношения.
3) Суперпозиция обратных отношений.
Определение 11.
Пусть на множестве A задано бинарное отношение 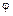 , тогда отношением, обратным к
, тогда отношением, обратным к 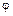 , называется отношение
, называется отношение 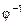 , также заданное на A, которое состоит из тех и только тех пар
, также заданное на A, которое состоит из тех и только тех пар 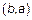 , для которых справедливо, что
, для которых справедливо, что 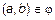 .
.
ПРИМЕР 7.
Пусть на множестве A={0,1,2,3} задано бинарное отношение 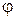 ={(0,1); (2,3); (1,3)}, тогда
={(0,1); (2,3); (1,3)}, тогда 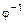 = {(1,0); (3,2); (3,1)}.
= {(1,0); (3,2); (3,1)}.
Для обратных отношений справедливы следующие равенства:
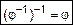 ,
, 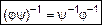 . (4)
. (4)
Заключение
|
- отношение на множестве есть множество;
- бинарные отношения могут быть заданы на декартовом произведении множеств;
- отношения могут быть рефлексивными, симметричными, антисимметричными и транзитивными;
- над отношениями можно делать такие же операции, как и над множествами;
- суперпозиция определяет новое связное множество;
- операция суперпозиции не коммутативна.
Литература
1. Яблонский Я. В. Введение в дискретную математику. – М.: Высшая школа, 2001. - 384 с.
2. Москинова Г.И. «Дискретная математика». – М.: Логос, 2002. – 240 с.
3. Ильин В.А., Позняк Э.Г. «Л инейная алгебра». – М.: Физматлит, 2001.
4. Самсонов Б.Б. и др. «Компьютерная математика». – Ростов-на-Дону: Феникс, 2002. – 512 с.
Лекция 4
29
Дата: 2018-12-21, просмотров: 603.