Вариант 1
1. Что такое стереометрия.
2. Какие прямые в пространстве называются параллельными?
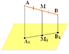
3. Дана плоскость β и прямые а. в и с. Известно, что одна из данных прямых параллельна плоскости β. Назовите эту прямую, если прямая а параллельна прямой с, прямые в и с пересекаются, а прямая с лежит в плоскости 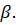 Сделайте рисунок и прокомментируйте его с помощью математических знаков.
Сделайте рисунок и прокомментируйте его с помощью математических знаков.
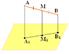
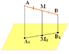
4. Через точки А, В и середину М отрезка АВ проведены параллельные прямые, пересекающие некоторую плоскость α в точках А1, В1, М1 соответственно. Найти длину отрезка ММ1, если АА1=13м, ВВ1=7м, причём отрезок АВ не пересекает плоскость α.
5. Через конец А отрезка АВ проведена плоскость. Через конец В и точку С этого отрезка проведены параллельные прямые В1 и С1. Найдите длину отрезка ВВ1, если СС1=21 см, АС : ВС = 3 : 4.
Вариант 2
1. Назовите основные фигуры в пространстве.
2. Какие прямые в пространстве называются скрещивающимися?
3. Дана плоскость β и прямые а, в и с. Известно, что одна из данных прямых параллельна плоскости β. Назовите эту прямую, если прямая в параллельна прямой с, прямые а и в пересекаются, а прямая с лежит в плоскости 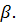 Сделайте рисунок и прокомментируйте его с помощью математических знаков.
Сделайте рисунок и прокомментируйте его с помощью математических знаков.
4. Через точки А, В и середину М отрезка АВ проведены параллельные прямые, пересекающие некоторую плоскость α в точках А1, В1, М1 соответственно. Найти длину отрезка ММ1, если АА1=3м, ВВ1=17м, причём отрезок АВ не пересекает плоскость α.
5. Через конец А отрезка АВ проведена плоскость. Через конец В и точку С этого отрезка проведены параллельные прямые В1 и С1. Найдите длину отрезка ВВ1, если
СС1=26 см, АВ : АС = 15 : 13.
Вариант 3
1. Сформулируйте теорему о трёх точках?
2. Что значит: прямая и плоскость параллельны?
3. Дана плоскость β и прямые а, в и с, причём две из трёх данных прямых параллельны. Назовите параллельные прямые, если прямая а лежит в плоскости β, прямая в параллельна плоскости β, а прямая с пересекает плоскость β. Сделайте рисунок и прокомментируйте его с помощью математических знаков.
4. Через концы отрезка АВ и его середину М отрезка АВ проведены параллельные прямые, пересекающие некоторую плоскость α в точках А1, В1 и М1. Найти длину отрезка ММ1, если отрезок АВ не пересекает плоскость α и если АА1=10м, ВВ1=14м.
5. Через конец А отрезка АВ проведена плоскость. Через конец В и точку С этого отрезка проведены параллельные прямые В1 и С1. Найдите длину отрезка ВВ1, если
АВ=8 см, АС : СС1 = 2 : 3.
Вариант 4
1. Сформулируйте теорему о прямой и точке.
2. Какие плоскости называются параллельными?
3. Дана плоскость β и прямые а, в и с, причём две из трёх данных прямых параллельны. Назовите параллельные прямые, если прямая а лежит в плоскости β, а прямые в и с пересекают плоскость β. Сделайте рисунок и прокомментируйте его с помощью математических знаков.
4. Через концы отрезка АВ и его середину М отрезка АВ проведены параллельные прямые, пересекающие некоторую плоскость α в точках А1, В1 и М1. Найти длину отрезка ММ1, если отрезок АВ не пересекает плоскость α и если АА1=12м, ВВ1=8м.
5. Через конец А отрезка АВ проведена плоскость. Через конец В и точку С этого отрезка проведены параллельные прямые В1 и С1. Найдите длину отрезка ВВ1, если
СС1=14 см, АВ : ВС = 10 : 3.
Ответы
| Вариант 1 | Вариант 2 | Вариант 3 | Вариант 4 | |||||||||
| 1 | Стереометрия – это раздел геометрии, в ко-тором изучаются фигу-ры в пространстве. | Основными фигурами в пространстве являются точка, прямая и плос-кость. | Через три точки, не ле-жащие на одной пря-мой, можно провести плоскость, и притом только одну. | Через прямую и не ле-жащую на ней точку можно провести плос-кость, и при том только одну. | ||||||||
| 2 | Две прямые в пространс-тве называются парал-лельными, если они ле-жат в одной плоскости и не пересекаются. | Прямые, которые не пе-ресекаются и не лежат в одной плоскости, назы-ваются скрещивающи-мися. | Прямая и плоскость параллельны – значит, они не пересекаются, то есть не имеют общих точек. | Две плоскости называ-ются параллельными, если они не пересека-ются, то есть не имеют общих точек. | ||||||||
| 3 | а 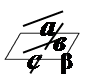 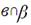
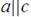 ; ; 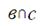 ; ; 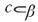 ; ; 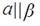
| в 
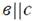 ; ; 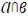 ; ; 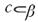 ; ; 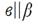
|  аив; аив; 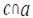
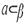 ; ; 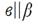 ; ; 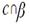 ; ; 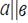
| 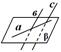 вис вис
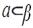 ; ; 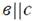 ; ; 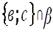
| ||||||||
| 4 |
ММ1- средняя линия;
|
ММ1- средняя линия;
|
ММ1- средняя линия;
|
ММ1- средняя линия;
| ||||||||
| 5 |
|
|
|
|
Контрольная работа №9
Векторы.
Часть 1.
Вариант № 1
1. Что называется вектором в пространстве?
2. Дайте определение действий над векторами: скалярного произведения.
3. Дайте определение координат вектора с началом в точке А1(х1; у1; z 1) и концом в точке А2(х2; у2; z 2).
4. Какие вектора называются равными.
5. Какие вектора называются противоположно направленными?
Вариант № 2
1. Какие вектора называются коллиниарными?
2. Что такое абсолютная величина вектора?
3. Какие вектора называются одинаково направленными?
4. Дайте определение действий над векторами: сложения и умножения.
5. Что такое нулевой вектор?
Часть 2.
Вариант № 1
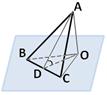
1. Сторона равностороннего треугольника равна 12 см. Найти площадь его ортогональной проекции на плоскость, которая образует с плоскостью 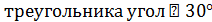 .
.
2. Даны точки А(0;0;7), В(1;4;2), С(0;4;5), D(4;2;0). Какие из этих точек лежат:
1) в плоскости ху; 2) на оси z ; 3) в плоскости у z .
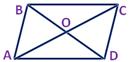
3. Докажите, что четырёхугольник АВСD с вершинами в точках А(0;2;-3),
В(-1;1;1), С(2;-2;-1), D(3;-1;-5).
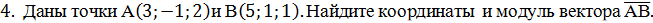
5. Даны точки А(1;-1;3), В(3;-1;1) и С(-1;1;3). Вычислите угол между векторами
 .
.
Вариант № 2
1. Дан прямоугольный треугольник с катетами 6 и 9 см. Найти площадь его ортогональной проекции на плоскость, которая образует с плоскостью 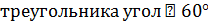 .
.
2. Даны точки А(0;6;0), В(0;3;3), С(3;4;8), D(1;0;9). Какие из этих точек лежат:
1) в плоскости х z ; 2) на оси у; 3) в плоскости у z .
3. Докажите, что четырёхугольник АВСD с вершинами в точках А(2;1;3),
В(1;0;7), С(-2;1;5), D(-1;2;1).
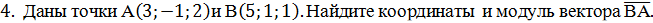
5. Даны точки А(1;3;0), В(2;3;-1) и С(1;2;-1). Вычислите угол между векторами
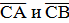 .
.
ОТВЕТЫ
| № варианта № задания | Вариант № 1 | Вариант № 2 |
| 1. | Вектором в пространстве называется направленный отрезок. | Два ненулевых вектора называются коллиниарными, если они лежат на одной прямой или на параллельных прямых. |
| 2. | Скалярным произведением векторов
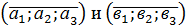 называется число
а1в1+ а2в2+ а3в3. называется число
а1в1+ а2в2+ а3в3.
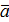 ∙ ∙ 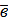 = = 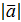 ∙ ∙ 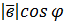 . .
| Абсолютной величиной вектора
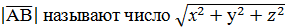 . .
|
| 3. | Координатами вектора с началом в точке А1(х1; у1; z 1) и концом в точке А2(х2; у2; z 2) называются числа х2 - х1; у2 - у1; z 2 - z 1 . | 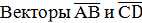 называются одинаково направленными, если полупрямые АВ и СD одинаково направлены. называются одинаково направленными, если полупрямые АВ и СD одинаково направлены.
|
| 4. | Вектора называются равными, если они сонаправлены и их длины равны (если они совмещаются параллельным переносом). У равных векторов соответствующие координаты равны. | Суммой векторов 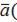 а1;а2;а3) и а1;а2;а3) и 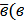 1; 1; 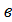 2; 2;  3) называют вектор 3) называют вектор
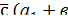 1; 1; 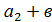 2; 2; 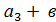 3).
Произведением вектора 3).
Произведением вектора
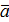 (а1; а2; а3) на число λ называется вектор λ (а1; а2; а3) на число λ называется вектор λ 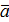 = = 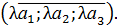 Если λ>0,то направление совпадает с направлением вектора
Если λ>0,то направление совпадает с направлением вектора 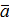 ; если λ<0, то направление противоположно направлению вектора ; если λ<0, то направление противоположно направлению вектора 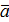 . .
|
| 5. | 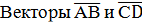 называются противоположно направленными, если полупрямые АВ и СD противоположно направлены. называются противоположно направленными, если полупрямые АВ и СD противоположно направлены.
| Любая точка в пространстве может рассматриваться как вектор. Такой вектор называется нулевым. |
ОТВЕТЫ
| № варианта № задания | Вариант № 1 | Вариант № 2 | ||||
| 1. |
|
| ||||
| 2. | 1) в ху: D; 2) на оси z : А; 3) в у z : А; С. | 1) в х z : D; 2) на оси у: А; 3) в у z : А; В. | ||||
| 3. | Воспользуемся формулами для координат середины отрезка в пространстве.
 АС: х=
АС: х= 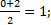 у= у= 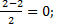 z = z = 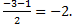 ВD: х=
ВD: х= 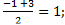 у= у= 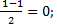 z = z = 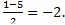 Координаты середины отрезков АС и ВD совпадают, поэтому диагонали АС и ВD четырёхугольника АВСD пересекаются и точкой пересечения делятся пополам, следовательно четырёхугольник АВСD – параллелограмм.
Координаты середины отрезков АС и ВD совпадают, поэтому диагонали АС и ВD четырёхугольника АВСD пересекаются и точкой пересечения делятся пополам, следовательно четырёхугольник АВСD – параллелограмм.
| Воспользуемся формулами для координат середины отрезка в пространстве.
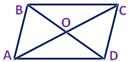 АС: х=
АС: х= 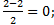 у= у= 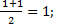 z = z = 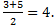 ВD: х=
ВD: х= 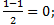 у= у= 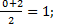 z = z = 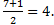 Координаты середины отрезков АС и ВD совпадают, поэтому диагонали АС и ВD четырёхугольника АВСD пересекаются и точкой пересечения делятся пополам, следовательно четырёхугольник АВСD – параллелограмм.
Координаты середины отрезков АС и ВD совпадают, поэтому диагонали АС и ВD четырёхугольника АВСD пересекаются и точкой пересечения делятся пополам, следовательно четырёхугольник АВСD – параллелограмм.
| ||||
| 4. | 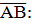 5 – 3 = 2; 1 – (-1) = 2; 1 - 2 = -1. 5 – 3 = 2; 1 – (-1) = 2; 1 - 2 = -1.
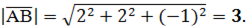
| 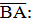 3 – 5 = -2; -1 – 1 = -2; 2 – 1 = 1. 3 – 5 = -2; -1 – 1 = -2; 2 – 1 = 1.
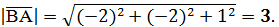
| ||||
| 5. | 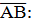 3-1 = 2; -1 – (-1) = 0; 1 – 3 = -2. 3-1 = 2; -1 – (-1) = 0; 1 – 3 = -2.
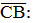 3 – (-1) = 4; -1 – 1 = -2; 1 – 3 = -2. 3 – (-1) = 4; -1 – 1 = -2; 1 – 3 = -2.
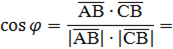
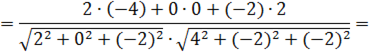
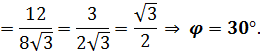
| 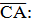 1 – 1 = 0; 3 – 2 = 1; 0 – (-1) = 1. 1 – 1 = 0; 3 – 2 = 1; 0 – (-1) = 1.
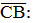 1 – 2 = -1; 3 – 2 = 1; -1 – (-1) = 0. 1 – 2 = -1; 3 – 2 = 1; -1 – (-1) = 0.
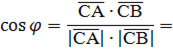
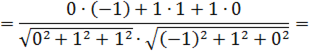
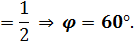
|
Контрольная работа №10.
Дата: 2018-12-21, просмотров: 1947.

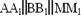
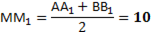
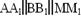
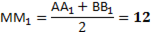
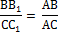
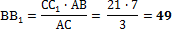
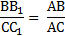
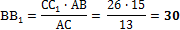
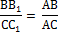
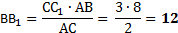
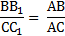
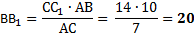
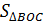 =
= 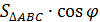
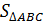 =
= 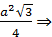
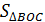 =
= 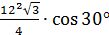 =
= 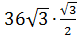 =54(см2)
=54(см2)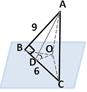
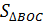 =
= 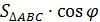
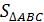 =
= 
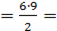 27
27
 13,5(см2)
13,5(см2)