Бурятский респотребсоюз

КОМПЛЕКТ КОНТРОЛЬНО-ОЦЕНОЧНЫХ СРЕДСТВ
ДЛЯ ОЦЕНКИ РЕЗУЛЬТАТОВ ОСВОЕНИЯ ПРОГРАММЫ
УЧЕБНОЙ ДИСЦИПЛИНЫ ОУД.03 «МАТЕМАТИКА»
2018
Комплект контрольно-оценочных средств оценки результатов освоения программы ОУД.03 Математика разработан на основе Федерального государственного образовательного стандарта среднего профессионального образования по специальностям СОО 40.02.01 Право и организация социального обеспечения; 38.02.04 Коммерция; 38.02.07 Банковское дело; 38.02.01 Экономика и бухгалтерский учет (по отраслям), 38.02.05. Товароведение и экспертиза качества потребительских товаров, 38.08.06 Финансы, 43.02.11 Гостиничный сервис, 38.02.03 Операционная деятельность в логистике
Организация – разработчик:
ПОЧУ «Улан-Удэнский торгово-экономический техникум»
Разработчик:
З.Жаргалсайхан, С.Б. Бадмацыренова – преподаватели математики ТЭТ
СОДЕРЖАНИЕ
1. Паспорт комплекта контрольно-оценочных средств. 4
1.1. Область применения.. 4
1.2 Система контроля и оценки освоения программы учебной дисциплины... 9
1.3. Результаты освоения учебной дисциплины, подлежащие проверке.. 10
2. Комплект материалов для оценки сформированности умений и знаний. 22
2.1 Задания для текущего контроля.. 22
2.3 Комплект материалов для промежуточной аттестации. 78
Паспорт комплекта контрольно-оценочных средств
Область применения
Учебный предмет «Математика» является интегративным, содержит: алгебру и начала математического анализа, геометрию, и основы теории вероятности
Задачами реализации программы учебного предмета «Математика» (базовый уровень) являются:
1) формирование представлений о математике как части мировой культуры и о месте математики в современной цивилизации, о способах описания на математическом языке явлений реального мира;
2) формирование представлений о математических понятиях как о важнейших математических моделях, позволяющих описывать и изучать разные процессы и явления; понимание возможности аксиоматического построения математических теорий;
3) овладение методами доказательств и алгоритмов решения; умение их применять, проводить доказательные рассуждения в ходе решения задач;
4) овладение стандартными приемами решения рациональных и иррациональных, показательных, степенных, тригонометрических уравнений и неравенств, их систем; использование готовых компьютерных программ, в том числе для поиска пути решения и иллюстрации решения уравнений и неравенств;
5) формирование представлений об основных понятиях, идеях и методах математического анализа;
6) овладение основными понятиями о плоских и пространственных геометрических фигурах, их основных свойствах; формирование умения распознавать на чертежах, моделях и в реальном мире геометрические фигуры; применение изученных свойств геометрических фигур и формул для решения геометрических задач и задач с практическим содержанием;
7) формирование представлений о процессах и явлениях, имеющих вероятностный характер, о статистических закономерностях в реальном мире, об основных понятиях элементарной теории вероятностей; умений находить и оценивать вероятности наступления событий в простейших практических ситуациях и основные характеристики случайных величин;
8) овладение навыками использования готовых компьютерных программ при решении задач.
Задачами реализации программы учебного предмета «Математика» (углубленный уровень) являются:
1) формирование представлений о необходимости доказательств при обосновании математических утверждений и роли аксиоматики в проведении дедуктивных рассуждений;
2) формирование понятийного аппарата по основным разделам курса математики; знаний основных теорем, формул и умения их применять; умения доказывать теоремы и находить нестандартные способы решения задач;
3) формирование умений моделировать реальные ситуации, исследовать построенные модели, интерпретировать полученный результат;
4) формирование представлений об основных понятиях математического анализа и их свойствах, владение умением характеризовать поведение функций, использование полученных знаний для описания и анализа реальных зависимостей;
5) овладение умениями составления вероятностных моделей по условию задачи и вычисления вероятности наступления событий, в том числе с применением формул комбинаторики и основных теорем теории вероятностей; исследования случайных величин по их распределению.
1.2 Система контроля и оценки освоения программы учебной дисциплины
Система контроля и оценки освоения учебной дисциплины «Математика» соответствует «Положению о текущем, рубежном контроле и промежуточной аттестации обучающихся в ПОЧУ «Улан-Удэнский торгово-экономический техникум» и рабочим учебным планам.
Текущий и рубежный контроль успеваемости, промежуточная аттестация по дисциплине проводится с целью определения степени соответствия уровня освоения образовательных результатов требованиям работодателей, предъявляемых к специалисту среднего звена (менеджер, банкир, коммерсант, финансист, бухгалтер, юрист, товаровед, логист).
Текущий контроль успеваемости обучающихся – это систематическая проверка усвоения образовательных результатов, проводимая преподавателем на текущих занятиях согласно расписанию учебных занятий в соответствии с ППССЗ по специальности. Он осуществляется различными способами и приемами – фронтальный опрос, развернутые ответы по теме занятия, выполнение заданий по карточкам у доски, краткие письменные ответы, выполнение практических, проблемных заданий, тестовые задания по отдельным темам, разделам.
Рубежный контроль - процедура, проводимая с целью оценки качества освоения обучающимися содержания части учебной дисциплины в рамках накопительной системы оценивания за определенный промежуток времени.
Промежуточная аттестация является заключительным этапом контроля результатов деятельности студентов при изучении учебной дисциплины.
Промежуточная аттестация проводится в форме экзамена, который преследует цель оценить освоение образовательных результатов по дисциплине. Условиями допуска к экзамену являются положительные результаты рубежного контроля и выполненные СРС работы по курсу дисциплины.
Комплект материалов для оценки сформированности умений и знаний представлен в виде экзаменационных билетов.
Контроль за достижением образовательных результатов осуществляется в форме стартовой (входной) диагностики, текущего, тематического контроля и промежуточной аттестации.
В рамках стартовой (входной) диагностики проводится входная контрольная работа.
Содержание, формы и периодичность текущего контроля определяются преподавателем с учетом степени сложности изучаемого материала, а также особенностей обучающихся. Основными формами текущего контроля являются устный и письменный опросы, контрольные работы, диктанты, тесты, проверочные работы, комплексный анализ текстов, практические задания.
| Обязательные формы и методы контроля (аудиторная деятельность) | Самостоятельная работа обучающихся |
| Текущая аттестация: | |
| устный опрос | логические задания, подготовка презентаций |
| выполнение логических заданий | практические задания |
| защита индивидуальных проектных работ | выполнение проектов |
| тестирование | логические задания |
| письменная самостоятельная работа | практические задания |
| Итоговая аттестация: | экзамен |
Тематика индивидуальных проектных работ
1. Загадочное число «Пи». История образования числа «Пи».
2. Теорема Виета. Примеры решений задач с помощью теоремы Виета.
3. Арифметическая и геометрическая прогрессии. Свойства и примеры.
4. Решение системы линейных уравнений. Алгебраическое и графическое решение.
5. Решение системы линейных неравенств. Алгебраическое и графическое решение.
6. Решение системы логарифмических уравнений. Алгебраическое и графическое решение.
7. Решение системы логарифмических неравенств. Алгебраическое и графическое решение.
8. Решение системы показательных уравнений. Алгебраическое и графическое решение.
9. Решение системы показательных неравенств. Алгебраическое и графическое решение.
10. Решение системы квадратных уравнений. Алгебраическое и графическое решение.
11. Решение системы квадратных неравенств. Алгебраическое и графическое решение.
12. Практическое применение тригонометрических функций.
13. Основные методы решения тригонометрических уравнений.
14. Вычисление площади плоских фигур с помощью определенного интеграла.
15. Другие способы применения интегралов в жизни.
16. Векторы в школьном курсе «Геометрия». Практическое применение.
17. Правильный 7-ми угольник. Построение и свойства.
18. Правильный 8-ми угольник. Построение и свойства.
19. Изготовление звёздчатого октаэдра.
20. Изготовление малого звёздчатого додекаэдра.
21. Изготовление додекаэдра и октаэдра.
22. Изготовление икосаэдра и гексаэдра.
23. Решение нестандартных задач теории вероятностей.
24. Великие математики и их роль в развитии математики.
25. Бином Ньютона и треугольник Паскаля.
1.3. Результаты освоения учебной дисциплины, подлежащие проверке
Комплекс контрольно-оценочных средств позволяет оценивать освоение умений и усвоение знаний.
Реализация рабочей программы направлена на достижение личностных, предметных и метапредметных образовательных результатов в соответствии с требованиями ФГОС СОО:
К важнейшим личностным результатам освоения ООП, в т.ч. дисциплины Математика относятся следующие убеждения и качества:
- готовность и способность обучающихся к саморазвитию и личностному самоопределению;
- готовность и способность к образованию, в том числе самообразованию, на протяжении всей жизни; сознательное отношение к непрерывному образованию как условию успешной профессиональной и общественной деятельности;
- сформированность их мотивации к обучению и целенаправленной познавательной деятельности.
Метапредметные результаты освоения ООП, в т.ч. дисциплины Математика выражаются в следующих качествах:
- освоенные обучающимися межпредметные понятия и универсальные учебные действия (регулятивные, познавательные, коммуникативные), способность их использования в познавательной и социальной практике;
- самостоятельность в планировании и осуществлении учебной деятельности и организации учебного сотрудничества с педагогами и сверстниками;
- способность к построению индивидуальной образовательной траектории, владение навыками учебно-исследовательской, проектной и социальной деятельности
Предметные результаты изучения Математики. Соответственно, выделяются три направления требований к результатам математического образования:
1) практико-ориентированное математическое образование (математика для жизни);
2) математика для использования в профессии;
3) творческое направление, на которое нацелены те обучающиеся, которые планируют заниматься творческой и исследовательской работой в области математики, физики, экономики и других областях.
Эти направления реализуются в двух блоках требований к результатам математического образования.
На базовом уровне:
Выпускник научится : для использования в повседневной жизни и обеспечения возможности успешного продолжения образования по специальностям, не связанным с прикладным использованием математики.
Выпускник получит возможность научиться : для развития мышления, использования в повседневной жизни и обеспечения возможности успешного продолжения образования по специальностям, не связанным с прикладным использованием математики.
На углубленном уровне:
Выпускник научится : для успешного продолжения образования по специальностям, связанным с прикладным использованием математики.
Выпускник получит возможность научиться: для обеспечения возможности успешного продолжения образования по специальностям, связанным с осуществлением научной и исследовательской деятельности в области математики и смежных наук.
В соответствии с Федеральным законом «Об образовании в РФ» (ст. 12 п. 7) организации, осуществляющие образовательную деятельность, реализуют эти требования в образовательном процессе с учетом настоящей примерной основной образовательной программы  как на основе учебно-методических комплектов соответствующего уровня, входящих в Федеральный перечень Министерства образования и науки Российской Федерации, так и с возможным использованием иных источников учебной информации (учебно-методические пособия, образовательные порталы и сайты и др.)
как на основе учебно-методических комплектов соответствующего уровня, входящих в Федеральный перечень Министерства образования и науки Российской Федерации, так и с возможным использованием иных источников учебной информации (учебно-методические пособия, образовательные порталы и сайты и др.)
Цели освоения программы базового уровня – обеспечение возможности использования математических знаний и умений в повседневной жизни и возможности успешного продолжения образования по специальностям, не связанным с прикладным использованием математики.
Обучающиеся, осуществляющие обучение на базовом уровне, должны освоить общие математические умения, необходимые для жизни в современном обществе; вместе с тем они получают возможность изучить предмет глубже, с тем, чтобы в дальнейшем при необходимости изучать математику для профессионального применения.
При изучении математики на углубленном уроне предъявляются требования, соответствующие направлению «математика для профессиональной деятельности»; вместе с тем выпускник получает возможность изучить математику на гораздо более высоком уровне, что создаст фундамент для дальнейшего серьезного изучения математики в вузе.
При изучении математики большое внимание уделяется развитию коммуникативных умений (формулировать, аргументировать и критиковать), формированию основ логического мышления в части проверки истинности и ложности утверждений, построения примеров и контрпримеров, цепочек утверждений, формулировки отрицаний, а также необходимых и достаточных условий. В зависимости от уровня программы больше или меньше внимания уделяется умению работать по алгоритму, методам поиска алгоритма и определению границ применимости алгоритмов. Требования, сформулированные в разделе «Геометрия», в большей степени относятся к развитию пространственных представлений и графических методов, чем к формальному описанию стереометрических фактов.
Задания для текущего контроля (см. далее)
2.2 Критерии оценки
Требования к реферату:
Правильность оформления (титульный лист, содержание, введение, основная часть, заключение, список литературы, ссылки).
Содержательная часть (полнота раскрытия темы).
Самостоятельное выполнение работы.
Критерии оценивания реферата / презентации:
| Критерии оценки Оценка | Содержательная часть работы | Оформление работы | ||||||
| 90-100% | 70-90% | 50-70% | менее 50% | 90-100% | 70-90% | 50-70% | менее 50% | |
| 5 | + | + | ||||||
| 4 | + | + | ||||||
| 4 | + | + | ||||||
| 3 | + | + | ||||||
| 3 | + | + | ||||||
| 3 | + | + | ||||||
| 2 | + | |||||||
| 2 | + | + | ||||||
Критерии оценки за устные ответы:
Глубина и полнота ответа. Формулирование собственных выводов. Проявление активности. Навыки публичного выступления
| Критерии оценки Оценка | Правильность и полнота ответа на вопросы | |||
| 90-100% | 70-90% | 50-70% | менее 50% | |
| 5 | + | |||
| 4 | + | |||
| 3 | + | |||
| 2 | + | |||
Письменная домашняя работа
Критерии оценки:
Глубина и полнота ответа.
Формулирование собственных выводов.
| Критерии оценки Оценка | Правильность и полнота письменной работы | |||
| 90-100% | 70-90% | 50-70% | менее 50% | |
| 5 | + | |||
| 4 | + | |||
| 3 | + | |||
| 2 | + | |||
Критерии оценивания тестовых заданий:
| Тесты | 50-65% - 3 балла - оценка «3» 66-84 % - 4 балла - оценка «4» 85-100 % - 5 баллов - оценка «5» |
Требования к сообщению:
1. Длительность выступления - в пределах 5 минут.
2. Общая культура выступления.
3. Содержательная часть.
4. Наличие презентации (по возможности).
«5» - тема раскрыта, культура выступления высокая, наличие презентации.
«4» - тема раскрыта, культура выступления средняя, наличие презентации,
есть незначительные замечания.
«3» - тема раскрыта не полностью, культура выступления средняя, есть
замечания.
«2» - тема не раскрыта, культура выступления низкая, есть существенные
замечания.
Критерии оценки практического задания:
1. Правильное оформление работы в соответствие с предъявляемыми
требованиями.
1. Правильность и полнота ответа. Применение теоретических знаний для решений практических задач
2. Обоснованность ответа с ссылками на документы.
«5» - ответ правильный и полный с ссылками на документы.
«4» - есть незначительные неточности, присутствуют ссылки на документы.
«3» - ответ неполный, присутствуют ссылки на документы.
«2» - ответ неправильный (ответ отсутствует) или не даны ссылки на
документы.
Контрольная работа №1.
Вариант 1
1.Вычислить: (2-1 + 3-1)( 2-1 - 3-1) + (2-1 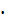 20)-4 : 23
20)-4 : 23
а)7 б) 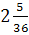 в)2
в)2 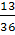 г) -3 д)1
г) -3 д)1 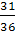
2.Найдите значение выражения
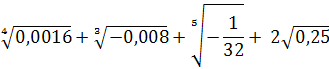
а)0,5 б) выражение не имеет смысла в) 101 г) 1,9 д) 1,5
3.При каких значениях х имеет смысл выражение 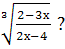
а) 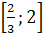 б)
б) 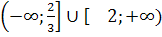 ь в) х
ь в) х 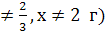 R д) другой ответ
R д) другой ответ
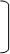
 4.Упростить выражение
4.Упростить выражение 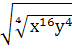 4 - (
4 - ( 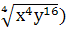 2
2
а)0 б) х2у2(х6 – у6) в)х6у6 г)х8у8 д) другой ответ
5.Вычислите 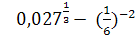 +
+ 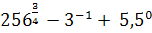
а)104 б) 32 в) 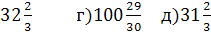
6) Упростить выражение 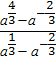
а) а+1 б) а-1 в) 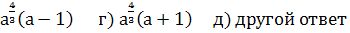
7.Вычислить 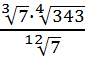
а) 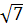 б)7 в)1 г)49 д) другой ответ
б)7 в)1 г)49 д) другой ответ
Вариант 2
1.Вычислить: (3-1 + 3-1)( 3-1 - 4-1) + (3-1 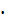 30)-4 : 33
30)-4 : 33
а)8 б) 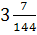 в)8,76 г) 3,04 д)3
в)8,76 г) 3,04 д)3 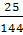
2.Найдите значение выражения
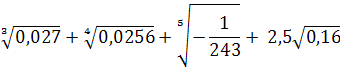
а) 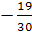 б)выражение не имеет смысла в)
б)выражение не имеет смысла в) 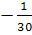 г)
г) 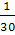 д) -
д) - 
3.При каких значениях х не имеет смысл выражение 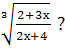
а) 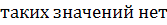 б)
б) 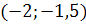
в) х 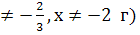 (-
(- 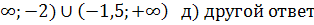
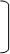
 4.Упростить выражение
4.Упростить выражение 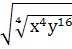 4 - (
4 - ( 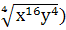 2
2
а)0 б)0 в) х2у2(х6 – у6) в)х6у6 г)х8у8 д) другой ответ
5.Вычислите 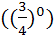 -1,5 – 7,5
-1,5 – 7,5 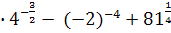
а)3 б) 5 в) 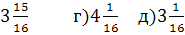
6) Упростить выражение 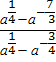
а) 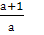 б)
б) 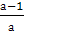 в)
в) 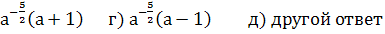
7.Вычислить 
а) 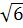 б)1 в)6 г)36 д) другой ответ
б)1 в)6 г)36 д) другой ответ
Контрольная работа №2.
Тригонометрические функции.
Вариант 1.
1. Найдите значение выражения: 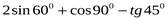
1) 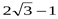 ; 2)
; 2) 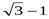 ; 3)
; 3) 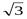 ; 4) 0.
; 4) 0.
2. Сравните с нулём выражения: sin 1200, cos 1950, ctg 3590.
Выберите правильную серию ответов:
1) + – – 2) – – + 3) + + – 4) + – +
3. Вычислите: 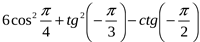
1) 12; 2) 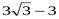 ; 3) 6; 4) 0.
; 3) 6; 4) 0.
4. Упростите выражение: 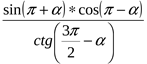
1) – cos2a; 2) cos2a; 3) sin2a; 4) – sin2a.
5. Упростите выражение: sina *cos a * ctg a – 1
1) 0; 2) cos2a; 3) – sin2a; 4) sin2a.
6. Упростите выражение: 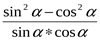
1) sin a – cos a; 2) –2 ctg 2a; 3) tg 2a; 4) 0,5 ctg 2a.
7. Вычислите: 2sin 150 * cos 150
1) 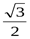 ; 2)
; 2)  ; 3)
; 3) 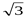 ; 4)
; 4)  .
.
8. Вычислите: cos 
1) 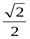 ; 2)
; 2) 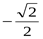 ; 3)
; 3) 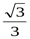 ; 4) 0.
; 4) 0.
9. Представив 1050 как 600 + 450, вычислите sin 1050.
1) 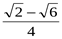 ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4) 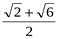 .
.
10. Дано: sin a = – 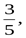 где
где 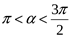 . Найдите tg 2a
. Найдите tg 2a
1) 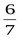 ; 2)
; 2) 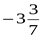 ; 3)
; 3) 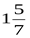 ; 4)
; 4) 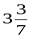 .
.
Вариант 2.
1. Найдите значение выражения: 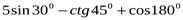
1) 2,5; 2) 0,5; 3) 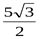 ; 4) 1,5.
; 4) 1,5.
2. Сравните с нулём выражения: sin 1870, cos 2150, tg 800.
Выберите правильную серию ответов:
1) + – + 2) – + + 3) – – + 4) – + –
3. Вычислите: 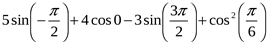
1) 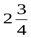 ; 2) -
; 2) -  ; 3) -
; 3) - 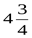 ; 4)
; 4)  .
.
4. Упростите выражение: 
1) tg2a; 2) -tg2a; 3) -ctg2a ; 4) ctg2a.
5. Упростите выражение: 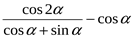
1) – sin a; 2) sin a; 3) – 2cos a; 4) sin a – 2cos a.
6. Упростите выражение: 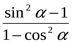
1) ctg2a; 2) tg2a; 3) – tg2a; 4) – ctg2a.
7. Вычислите: 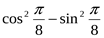 1)
1) 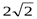 ; 2)
; 2) 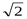 ; 3)
; 3) 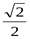 ; 4) 0.
; 4) 0.
8. Вычислите: cos  1500 1)
1500 1) 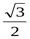 ; 2)
; 2) 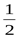 ; 3)
; 3) 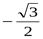 ; 4)
; 4) 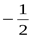 .
.
9. Представив 150 как 450 – 300, вычислите cos 150.
1) 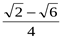 ; 2)
; 2)  ; 3)
; 3) 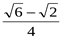 ; 4)
; 4) 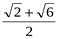 .
.
10. Дано: cos a = – 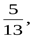 где
где  . Найдите ctg 2a
. Найдите ctg 2a
1) 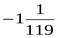 ; 2)
; 2) 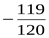 ; 3)
; 3) 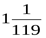 ; 4)
; 4) 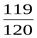 .
. 
Контрольная работа №3.
Функции и графики функций.
1 вариант
1. Найдите область определения функции 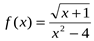 .
.
2. Найдите область значений функции 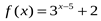 .
.
3. Найдите наименьшее значение функции 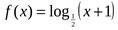 на отрезке
на отрезке 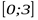 .
.
4. Исследуйте на чётность и нечетность функцию
а) 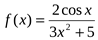 ; б)
; б) 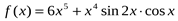 .
.
5. Постройте график функции 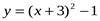 . Пользуясь графиком, найдите
. Пользуясь графиком, найдите
промежутки возрастания и убывания функции, экстремум функции.
6. Найдите функцию, обратную к функции 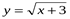 .
.
Постройте график данной функции и график обратной к данной функции;
укажите область определения и множество значений каждой из них.
2 вариант
1. Найдите область определения функции 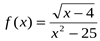 .
.
2. Найдите область значений функции 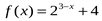 .
.
3. Найдите наибольшее значение функции 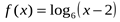 на отрезке
на отрезке 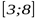 .
.
4. Исследуйте на чётность и нечетность функцию
а) 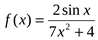 ; б)
; б) 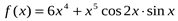 .
.
5. Постройте график функции 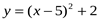 . Пользуясь графиком, найдите
. Пользуясь графиком, найдите
промежутки возрастания и убывания функции, экстремум функции.
6. Найдите функцию, обратную к функции 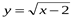 .
.
Постройте график данной функции и график обратной к данной функции;
укажите область определения и множество значений каждой из них.
3 вариант
1. Найдите область определения функции 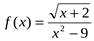 .
.
2. Найдите область значений функции 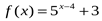 .
.
3. Найдите наименьшее значение функции 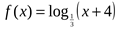 на отрезке
на отрезке 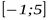 .
.
4. Исследуйте на чётность и нечетность функцию
а) 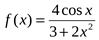 ; б)
; б) 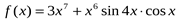 .
.
5. Постройте график функции 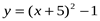 . Пользуясь графиком, найдите
. Пользуясь графиком, найдите
промежутки возрастания и убывания функции, экстремум функции.
6. Найдите функцию, обратную к функции 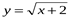 .
.
Постройте график данной функции и график обратной к данной функции;
укажите область определения и множество значений каждой из них.
4 вариант
1. Найдите область определения функции 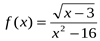 .
.
2. Найдите область значений функции 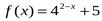 .
.
3. Найдите наибольшее значение функции 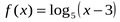 на отрезке
на отрезке 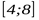 .
.
4. Исследуйте на чётность и нечетность функцию
а) 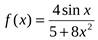 ; б)
; б) 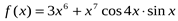 .
.
5. Постройте график функции 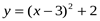 . Пользуясь графиком, найдите
. Пользуясь графиком, найдите
промежутки возрастания и убывания функции, экстремум функции.
6. Найдите функцию, обратную к функции 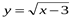 .
.
Постройте график данной функции и график обратной к данной функции;
укажите область определения и множество значений каждой из них.
ОТВЕТЫ
№
задания
1вариант
2 вариант
3 вариант
4 вариант
1
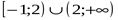
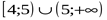
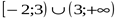
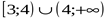
2
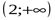
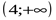
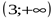

3
-2
1
-2
1
4а)
чётная
нечётная
чётная
нечётная
4б)
нечётная
чётная
нечётная
чётная
5
убывает

возрастает
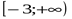

убывает
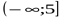
возрастает
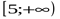

убывает

возрастает
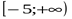

убывает
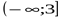
возрастает


6
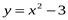 ,
, 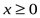
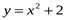 ,
, 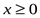
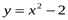 ,
, 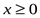
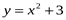 ,
, 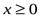
Контрольная работа №4
Вариант 1
1. Вычислить arccos(- 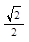 ) - arcsin
) - arcsin 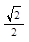 .
.
2. Решить неравенство tg х ≤ -1.
3. Решить уравнения
а) tg 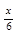 =0;
=0;
б) sin 2 х - 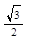 sin х=0;
sin х=0;
в) cos 2 х + cos х – 2 =0.
Вариант 2
1. Вычислить arctg (- 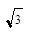 ) - arcsin
) - arcsin 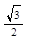 .
.
2. Решить неравенство cos х < 0.
3. Решить уравнения
а) cos (х - 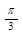 ) =
) = 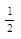 ;
;
б) tg 2 х - tg х=0;
в) sin 2 х + sin х – 2 =0.
Контрольная работа №5
ПРОИЗВОДНАЯ И ЕЁ ПРИЛОЖЕНИЕ
Вариант 1
1. Решить неравенство  ≥ 0.
≥ 0.
2. Тело движется по закону х( t )= t 3 -2 t 2 +5 (х – в метрах, t – в секундах). Найдите скорость и ускорение тела через 2с после начала движения.
3. Исследовать функцию f(х)= х2 + 7х – 4 на монотонность и экстремумы.
4. Найти наибольшее и наименьшее значения функции f(х)= х3- 6 х2 на
отрезке [-2;5].
5. Составьте уравнение касательной к графику функции f(х)= х2 + 2х в точке х0=1.
Вариант 2
1. Решить неравенство 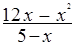 ≤ 0.
≤ 0.
2. Тело движется по закону х( t )= 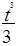 + 6 t - 1 (х – в метрах, t – в секундах). Найдите скорость и ускорение тела через 5с после начала движения.
+ 6 t - 1 (х – в метрах, t – в секундах). Найдите скорость и ускорение тела через 5с после начала движения.
3. Исследовать функцию f(х)=10 – 4х - х2 на монотонность и экстремумы.
4. Найти наибольшее и наименьшее значения функции f(х)= 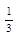 х3- х на
х3- х на
отрезке [0;4].
5. Составьте уравнение касательной к графику функции f(х)= х2-3х+2 в точке х0=
ОТВЕТЫ к контрольной работе «ПРОИЗВОДНАЯ И ЕЁ ПРИЛОЖЕНИЕ»
| № задания | Вариант 1 | Вариант 2 |
| 1 | [0; 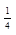 ] ] 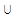 (7; ∞) (7; ∞)
| (-∞;0] 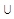 [5;12) [5;12)
|
| 2 | 4м/с; 8м/с2 | 31м/с; 10м/с2 |
| 3 | f ↓ на х 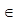 (-∞;-3,5),
f ↑ на х (-∞;-3,5),
f ↑ на х 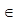 (-3,5; ∞)
х=-3,5 точка min (-3,5; ∞)
х=-3,5 точка min
| f ↑ на х 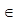 (-∞;-2),
f ↓ на х (-∞;-2),
f ↓ на х 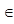 (-2; ∞)
х=-2 точка max (-2; ∞)
х=-2 точка max
|
| 4 | уmax=0; уmin=-32 [-2;5] [-2;5] | уmax= 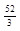 ; уmin= - ; уmin= - 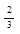 ;
[0;4] [0;4] ;
[0;4] [0;4]
|
| 5 | у=4х-1 | у = 1-5 х |
Контрольная работа №6
Интеграл и ее приложение
Вариант 1 Часть 1
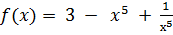 ;
2)
;
2) 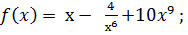 3)
3) 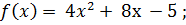 4)
4) 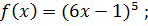 5)
5) 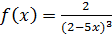 .
.
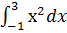 2)
2)  3)
3) 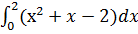 .
4)
.
4) 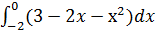 5)
5) 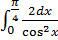
|
Вариант 2 Часть 1 | |
2. Найти общий вид первообразных:
1)  ;
2) ;
2) 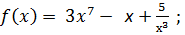 3)
3) 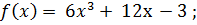 4)
4) 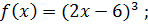 5)
5) 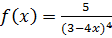 . .
| 2. Вычислить интегралы:
1) 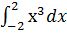 ;
2) ;
2) 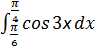 ;
3) ;
3) 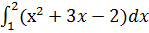 ;
4) ;
4) 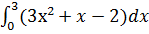 ;
5) ;
5) 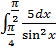 . .
|
Часть 2. Вариант 1
1. Найти общий вид первообразных для функции
a) f(x)= 4sin x + cos3x ;
б) f ( x )= x 2 + 2 x .
2. Найти первообразную функции f ( x )=5х + x 2 , график которой проходит через точку (1;3).
3. Вычислить интеграл 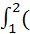 х2 +х)dx .
х2 +х)dx .
4. Вычислить площадь фигуры, ограниченной линиями
у = 3- х и у = - х2+2х+3.
Часть 2. Вариант2
1. Найти общий вид первообразных для функции
а ) f(x)= 3cos x + sin4x;
б) f ( x )= х5 + x 2 .
2. Найти первообразную функции f ( x )=3 x 2 -5, график которой проходит через точку (2;10).
3. Вычислить интеграл 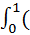 х2 +2х)dx
х2 +2х)dx
4. Вычислить площадь фигуры, ограниченной линиями
у = 3+2х и у = х2-2х+3.
| ОТВЕТЫ | ||
| Вариант1 | Вариант 2 | |
| 1. | 1) 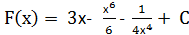 ;
2) ;
2) 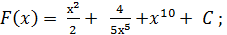 3)
3) 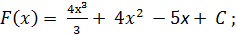 4)
4) 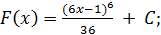 5)
5) 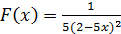 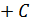 . .
| 1) 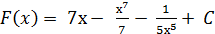 ;
2) ;
2) 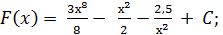 3)
3) 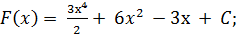 4)
4) 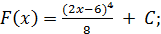 5)
5) 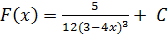 . .
|
| 2. | 1) 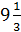 ;
2) 1 ;
3) ;
2) 1 ;
3)  ;
4) ;
4) 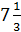 ;
5) 2. ;
5) 2.
| 1) 0 ;
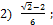
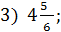 4) 25,5 ;
5) 5.
4) 25,5 ;
5) 5.
|
Ответы
| № варианта | Задание 1 а) | Задание 1 б) | Задание 2 | Задание 3 | Задание 4 |
| 1 | - 4 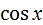 + +  +С +С
| 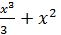 + С + С
| 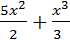 + + 
| 3 
| 4,5 |
| 2 | 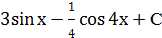
| 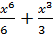 + С + С
| х3- 5х +12 | 1 
| 10 
|
Контрольная работа №7
Часть 1.
Вариант 1
1. Вычислите 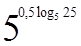 .
.
2. Найдите область определения функции у = lg 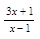 .
.
3. Решите уравнения:
а) log2 (4х - 1)= 3;
б) log7 2 = 1- log7 (5 - х).
4. Решите неравенства:
а) log5 (1 - 4х) ≤ 2;
б) log 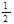 (2х + 3) > -3.
(2х + 3) > -3.
Вариант 2
1. Вычислите 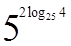 .
.
2. Найдите область определения функции у = lg 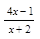 .
.
3. Решите уравнения:
а) log4 (2х - 1)= 2;
б) log2 (2х + 3) = log 2 4 + 1.
4. Решите неравенства: 
а) log3 (2 - 3х) ≥ 2;
б) 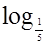 (х + 1) > -2.
(х + 1) > -2.
Вариант 3
1. Вычислите 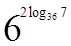 .
.
2. Найдите область определения функции у = lg 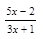 .
.
3. Решите уравнения:
а) log5 (6х - 1)= 2;
б) log3 (4х + 5) = log3 9 + 1.
4. Решите неравенства: 
а) log4 (2 - 5х) ≥ 3;
б) 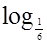 (х - 1) > -1.
(х - 1) > -1.
Вариант 4
1. Вычислите 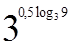 .
.
2. Найдите область определения функции у = lg 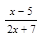 .
.
3. Решите уравнения:
а) log3 (7х - 2)= 2;
б) log7 (2х + 5) = log749 + 2.
4. Решите неравенства: 
а) log4 (5 - х) ≥ 0;
б) 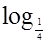 (3х - 1) > - 1 .
(3х - 1) > - 1 .
Вариант 5
1. Вычислите 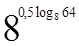 .
.
2. Найдите область определения функции у = lg 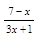 .
.
3. Решите уравнения:
а) 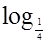 (х - 2)= - 2;
(х - 2)= - 2;
б) log5 (2х - 3) = log525 - 2.
4. Решите неравенства: 
а) log9 (3 - х) ≤ 0;
б) 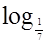 (3х - 1) < - 1 .
(3х - 1) < - 1 .
Вариант 6
1. Вычислите 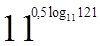 .
.
2. Найдите область определения функции у = lg 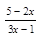 .
.
3. Решите уравнения:
а) 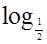 (х - 2)= - 3;
(х - 2)= - 3;
б) log8 (2х - 3) = log81 - 1.
4. Решите неравенства: 
а) log4 (8 - х) ≤ 2;
б) 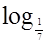 (2х - 1) < 0 .
(2х - 1) < 0 .
Вариант 7
1. Вычислите 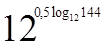 .
.
2. Найдите область определения функции у = lg 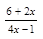 .
.
3. Решите уравнения:
а) 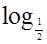 (2х - 1)= - 4;
(2х - 1)= - 4;
б) log3 (х - 3) = log327 - 1.
4. Решите неравенства: 
а) log5 (5 - х) ≤ 2;
б) 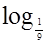 (х + 3) < - 1 .
(х + 3) < - 1 .
Вариант 8
1. Вычислите 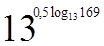 .
.
2. Найдите область определения функции у = lg 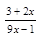 .
.
3. Решите уравнения:
а) 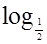 (х - 2)= 0;
(х - 2)= 0;
б) log3 (х + 9) = log381 - 3.
4. Решите неравенства: 
а) log5 (х - 6) ≤ 2;
б) 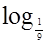 (х + 5) > - 2 .
(х + 5) > - 2 .
Вариант 9
1. Вычислите 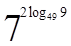 .
.
2. Найдите область определения функции у = lg 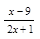 .
.
3. Решите уравнения:
а) log8 (5х - 2)= 1;
б) log6 (х + 5) = log6 36 + 1.
4. Решите неравенства: 
а) log5 (3 - х) ≥ 0;
Часть 2.
Вариант 1/5
1. Дайте определение логарифма данного числа по данному основанию.
2. 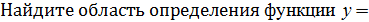
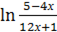
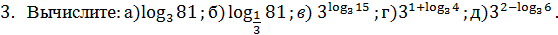
4. Найдите х, если 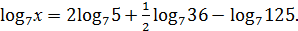
5. Вычислите 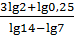 .
.
Вариант 2/6
1. Сформулируйте основные свойства логарифмов.
2. 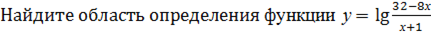 .
.
3. Вычислите: 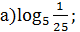
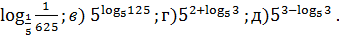
4. Найдите х, если 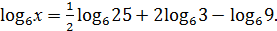
5. Вычислите 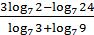 .
.
Вариант 3/7
1. Какая функция называется логарифмической? Сформулируйте основные свойства логарифмической функции при а>0.
2. 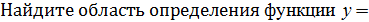
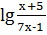 .
.
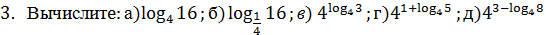
4. Найдите х, если 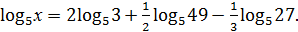
5. Вычислите 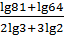 .
.
Вариант 4/8/9
1. Запишите основное логарифмическое тождество.
2. 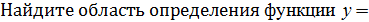
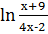 .
.
3. Вычислите: 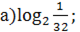
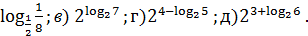
4. Найдите х, если 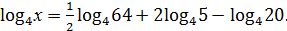
5. Вычислите 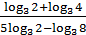 .
.
Часть 3.
Вариант 1-5
1. 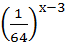 = 23-2х;
2. 7х+2 - 14∙7х = 5;
3. 49х - 8∙7х + 7 = 0;
4. = 23-2х;
2. 7х+2 - 14∙7х = 5;
3. 49х - 8∙7х + 7 = 0;
4. 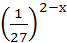 > 92х-1;
5. 10∙5х-1 + 5х+1 < 7. > 92х-1;
5. 10∙5х-1 + 5х+1 < 7.
|
Часть 3.
Вариант 6-9
1. 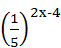 = 1253-4х;
2. 2х+4 - 2х = 120;
3. 36х - 4∙6х - 12 = 0;
4. = 1253-4х;
2. 2х+4 - 2х = 120;
3. 36х - 4∙6х - 12 = 0;
4. 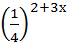 < 8х-1;
5. 8∙2х-1 - 2х > 48. < 8х-1;
5. 8∙2х-1 - 2х > 48.
|
Ответы «Логарифмы»
| № задания | Вариант 1 | Вариант 2 | Вариант 3 | Вариант 4 | Вариант 5 | Вариант 6 | Вариант 7 | Вариант 8 | Вариант 9 |
| 1 | 5 | 4 | 7 | 3 | 8 | 11 | 12 | 13 | 9 |
| 2 | (-∞;- 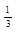 ) )
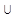 (1; ∞) (1; ∞)
| (-∞;-2) 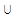 ( ( 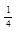 ;∞) ;∞)
| (-∞;- 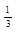 ) )
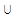 (0,4;∞) (0,4;∞)
| (-∞;-3,5)
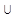 (5;∞) (5;∞)
| (- 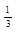 ;7) ;7)
| ( 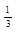 ;2,5) ;2,5)
| (-∞;-3)
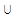 ( ( 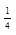 ;∞) ;∞)
| (-∞;-1,5)
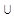 ( ( 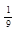 ;∞) ;∞)
| (-∞;-0,5)
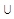 (9;∞) (9;∞)
|
| 3 а) | 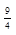
| 8,5 | 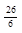
| 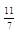
| 18 | 10 | 8,5 | 3 | 2 |
| 3 б) | 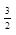
| 2,5 | 5,5 | 1198 | 2 | 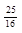
| 12 | -6 | 211 |
| 4 а) | [-6; 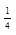 ) )
| (-∞;- 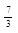 ] ]
| (-∞;-12,4] | (-∞;4] | [2;3) | [-8;8) | [-20;5) | (6;31] | (-∞;2] |
| 4 б) | (-1,5;2,5) | (-1;24) | (1; 7) | ( 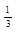 ; ; 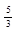 ) )
| ( 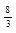 ;∞) ;∞)
| (1; ∞) | (6; ∞) | (-5;76) | (1;17) |
ОТВЕТЫ
«РЕШЕНИЕ ПОКАЗАТЕЛЬНЫХ УРАВНЕНИЙ И НЕРАВЕНСТВ»
| № варианта | Задание 1 | Задание 2 | Задание 3 | Задание 4 | Задание 5 |
| 1 | 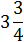
| -1 | 1; 0 | х < -4 | х < 0 |
| 2 | 
| 3 | 1 | х > 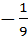
| х >4 |
ОТВЕТЫ к зачёту «Свойства логарифмов и логарифмической функции»
| № варианта Задание № | Вариант 1 | Вариант 2 | Вариант 3 | Вариант 4 |
| 1. | Логарифмом числа в по осно-ванию а называ-ется показатель степени, в кото-рую нужно воз-вести основание а, чтобы полу-чить число в.
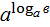 =в. =в.
| 1) 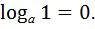 2)
2) 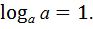 3)
3) 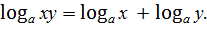 4)
4) 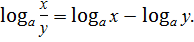 5)
5) 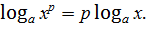
| Функцию, задан-
ную формулой
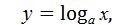 называют лога-рифмической функцией с ос-нованием а.
называют лога-рифмической функцией с ос-нованием а.
| 1) D( 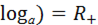 2) Е(
2) Е( 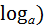 = = 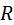 .
3) Логарифми-
ческая функция на всей области определения возрастает
(при а>0)
или убывает
(при 0<а<1). .
3) Логарифми-
ческая функция на всей области определения возрастает
(при а>0)
или убывает
(при 0<а<1).
|
| 2. | ( 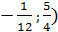
| (-1;4) | (-∞;-5) 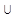 ( ( 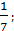 ∞) ∞)
| (-∞;-1) 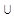 ( ( 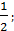 ∞) ∞)
|
| 3. | а) 4; б) -4; в) 15; г) 12; д) 1,5. | а) -2;
б) 4;
в) 125;
г) 75;
д) 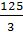 . .
| а) 2; б) -2; в) 3; г) 20; д) 8. | а) -5;
б) 3;
в) 7;
г) 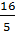 ;
д) 48. ;
д) 48.
|
| 4. | 
| 5 | 21 | 10 |
| 5. | 1 | 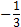
| 2 | 
|
Контрольная работа №8
Вариант 1
1. Что такое стереометрия.
2. Какие прямые в пространстве называются параллельными?
3. Дана плоскость β и прямые а. в и с. Известно, что одна из данных прямых параллельна плоскости β. Назовите эту прямую, если прямая а параллельна прямой с, прямые в и с пересекаются, а прямая с лежит в плоскости 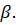 Сделайте рисунок и прокомментируйте его с помощью математических знаков.
Сделайте рисунок и прокомментируйте его с помощью математических знаков.
4. Через точки А, В и середину М отрезка АВ проведены параллельные прямые, пересекающие некоторую плоскость α в точках А1, В1, М1 соответственно. Найти длину отрезка ММ1, если АА1=13м, ВВ1=7м, причём отрезок АВ не пересекает плоскость α.
5. Через конец А отрезка АВ проведена плоскость. Через конец В и точку С этого отрезка проведены параллельные прямые В1 и С1. Найдите длину отрезка ВВ1, если СС1=21 см, АС : ВС = 3 : 4.
Вариант 2
1. Назовите основные фигуры в пространстве.
2. Какие прямые в пространстве называются скрещивающимися?
3. Дана плоскость β и прямые а, в и с. Известно, что одна из данных прямых параллельна плоскости β. Назовите эту прямую, если прямая в параллельна прямой с, прямые а и в пересекаются, а прямая с лежит в плоскости 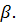 Сделайте рисунок и прокомментируйте его с помощью математических знаков.
Сделайте рисунок и прокомментируйте его с помощью математических знаков.
4. Через точки А, В и середину М отрезка АВ проведены параллельные прямые, пересекающие некоторую плоскость α в точках А1, В1, М1 соответственно. Найти длину отрезка ММ1, если АА1=3м, ВВ1=17м, причём отрезок АВ не пересекает плоскость α.
5. Через конец А отрезка АВ проведена плоскость. Через конец В и точку С этого отрезка проведены параллельные прямые В1 и С1. Найдите длину отрезка ВВ1, если
СС1=26 см, АВ : АС = 15 : 13.
Вариант 3
1. Сформулируйте теорему о трёх точках?
2. Что значит: прямая и плоскость параллельны?
3. Дана плоскость β и прямые а, в и с, причём две из трёх данных прямых параллельны. Назовите параллельные прямые, если прямая а лежит в плоскости β, прямая в параллельна плоскости β, а прямая с пересекает плоскость β. Сделайте рисунок и прокомментируйте его с помощью математических знаков.
4. Через концы отрезка АВ и его середину М отрезка АВ проведены параллельные прямые, пересекающие некоторую плоскость α в точках А1, В1 и М1. Найти длину отрезка ММ1, если отрезок АВ не пересекает плоскость α и если АА1=10м, ВВ1=14м.
5. Через конец А отрезка АВ проведена плоскость. Через конец В и точку С этого отрезка проведены параллельные прямые В1 и С1. Найдите длину отрезка ВВ1, если
АВ=8 см, АС : СС1 = 2 : 3.
Вариант 4
1. Сформулируйте теорему о прямой и точке.
2. Какие плоскости называются параллельными?
3. Дана плоскость β и прямые а, в и с, причём две из трёх данных прямых параллельны. Назовите параллельные прямые, если прямая а лежит в плоскости β, а прямые в и с пересекают плоскость β. Сделайте рисунок и прокомментируйте его с помощью математических знаков.
4. Через концы отрезка АВ и его середину М отрезка АВ проведены параллельные прямые, пересекающие некоторую плоскость α в точках А1, В1 и М1. Найти длину отрезка ММ1, если отрезок АВ не пересекает плоскость α и если АА1=12м, ВВ1=8м.
5. Через конец А отрезка АВ проведена плоскость. Через конец В и точку С этого отрезка проведены параллельные прямые В1 и С1. Найдите длину отрезка ВВ1, если
СС1=14 см, АВ : ВС = 10 : 3.
Ответы
| Вариант 1 | Вариант 2 | Вариант 3 | Вариант 4 | |||||||||
| 1 | Стереометрия – это раздел геометрии, в ко-тором изучаются фигу-ры в пространстве. | Основными фигурами в пространстве являются точка, прямая и плос-кость. | Через три точки, не ле-жащие на одной пря-мой, можно провести плоскость, и притом только одну. | Через прямую и не ле-жащую на ней точку можно провести плос-кость, и при том только одну. | ||||||||
| 2 | Две прямые в пространс-тве называются парал-лельными, если они ле-жат в одной плоскости и не пересекаются. | Прямые, которые не пе-ресекаются и не лежат в одной плоскости, назы-ваются скрещивающи-мися. | Прямая и плоскость параллельны – значит, они не пересекаются, то есть не имеют общих точек. | Две плоскости называ-ются параллельными, если они не пересека-ются, то есть не имеют общих точек. | ||||||||
| 3 | а 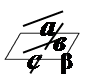 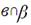
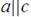 ; ; 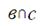 ; ; 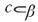 ; ; 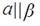
| в 
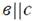 ; ; 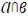 ; ; 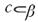 ; ; 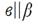
|  аив; аив; 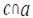
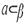 ; ; 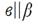 ; ; 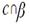 ; ; 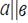
| 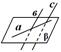 вис вис
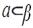 ; ; 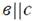 ; ; 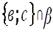
| ||||||||
| 4 |
ММ1- средняя линия;
|
ММ1- средняя линия;
|
ММ1- средняя линия;
|
ММ1- средняя линия;
| ||||||||
| 5 |
|
|
|
|
Контрольная работа №9
Векторы.
Часть 1.
Вариант № 1
1. Что называется вектором в пространстве?
2. Дайте определение действий над векторами: скалярного произведения.
3. Дайте определение координат вектора с началом в точке А1(х1; у1; z 1) и концом в точке А2(х2; у2; z 2).
4. Какие вектора называются равными.
5. Какие вектора называются противоположно направленными?
Вариант № 2
1. Какие вектора называются коллиниарными?
2. Что такое абсолютная величина вектора?
3. Какие вектора называются одинаково направленными?
4. Дайте определение действий над векторами: сложения и умножения.
5. Что такое нулевой вектор?
Часть 2.
Вариант № 1
1. Сторона равностороннего треугольника равна 12 см. Найти площадь его ортогональной проекции на плоскость, которая образует с плоскостью 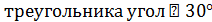 .
.
2. Даны точки А(0;0;7), В(1;4;2), С(0;4;5), D(4;2;0). Какие из этих точек лежат:
1) в плоскости ху; 2) на оси z ; 3) в плоскости у z .
3. Докажите, что четырёхугольник АВСD с вершинами в точках А(0;2;-3),
В(-1;1;1), С(2;-2;-1), D(3;-1;-5).
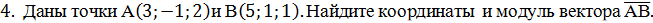
5. Даны точки А(1;-1;3), В(3;-1;1) и С(-1;1;3). Вычислите угол между векторами
 .
.
Вариант № 2
1. Дан прямоугольный треугольник с катетами 6 и 9 см. Найти площадь его ортогональной проекции на плоскость, которая образует с плоскостью 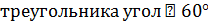 .
.
2. Даны точки А(0;6;0), В(0;3;3), С(3;4;8), D(1;0;9). Какие из этих точек лежат:
1) в плоскости х z ; 2) на оси у; 3) в плоскости у z .
3. Докажите, что четырёхугольник АВСD с вершинами в точках А(2;1;3),
В(1;0;7), С(-2;1;5), D(-1;2;1).
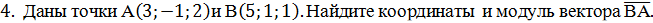
5. Даны точки А(1;3;0), В(2;3;-1) и С(1;2;-1). Вычислите угол между векторами
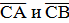 .
.
ОТВЕТЫ
| № варианта № задания | Вариант № 1 | Вариант № 2 |
| 1. | Вектором в пространстве называется направленный отрезок. | Два ненулевых вектора называются коллиниарными, если они лежат на одной прямой или на параллельных прямых. |
| 2. | Скалярным произведением векторов
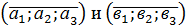 называется число
а1в1+ а2в2+ а3в3. называется число
а1в1+ а2в2+ а3в3.
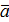 ∙ ∙ 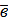 = = 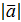 ∙ ∙ 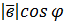 . .
| Абсолютной величиной вектора
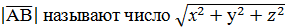 . .
|
| 3. | Координатами вектора с началом в точке А1(х1; у1; z 1) и концом в точке А2(х2; у2; z 2) называются числа х2 - х1; у2 - у1; z 2 - z 1 . | 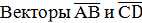 называются одинаково направленными, если полупрямые АВ и СD одинаково направлены. называются одинаково направленными, если полупрямые АВ и СD одинаково направлены.
|
| 4. | Вектора называются равными, если они сонаправлены и их длины равны (если они совмещаются параллельным переносом). У равных векторов соответствующие координаты равны. | Суммой векторов 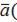 а1;а2;а3) и а1;а2;а3) и 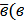 1; 1; 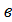 2; 2;  3) называют вектор 3) называют вектор
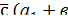 1; 1; 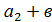 2; 2; 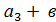 3).
Произведением вектора 3).
Произведением вектора
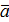 (а1; а2; а3) на число λ называется вектор λ (а1; а2; а3) на число λ называется вектор λ 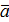 = = 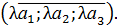 Если λ>0,то направление совпадает с направлением вектора
Если λ>0,то направление совпадает с направлением вектора 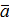 ; если λ<0, то направление противоположно направлению вектора ; если λ<0, то направление противоположно направлению вектора  . .
|
| 5. |  называются противоположно направленными, если полупрямые АВ и СD противоположно направлены. называются противоположно направленными, если полупрямые АВ и СD противоположно направлены.
| Любая точка в пространстве может рассматриваться как вектор. Такой вектор называется нулевым. |
ОТВЕТЫ
| № варианта № задания | Вариант № 1 | Вариант № 2 | ||||
| 1. |
|
| ||||
| 2. | 1) в ху: D; 2) на оси z : А; 3) в у z : А; С. | 1) в х z : D; 2) на оси у: А; 3) в у z : А; В. | ||||
| 3. | Воспользуемся формулами для координат середины отрезка в пространстве.
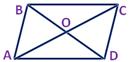 АС: х=
АС: х= 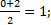 у= у= 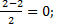 z = z = 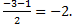 ВD: х=
ВD: х= 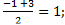 у= у= 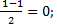 z = z =  Координаты середины отрезков АС и ВD совпадают, поэтому диагонали АС и ВD четырёхугольника АВСD пересекаются и точкой пересечения делятся пополам, следовательно четырёхугольник АВСD – параллелограмм.
Координаты середины отрезков АС и ВD совпадают, поэтому диагонали АС и ВD четырёхугольника АВСD пересекаются и точкой пересечения делятся пополам, следовательно четырёхугольник АВСD – параллелограмм.
| Воспользуемся формулами для координат середины отрезка в пространстве.
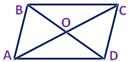 АС: х=
АС: х= 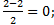 у= у= 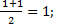 z = z = 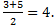 ВD: х=
ВD: х= 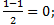 у= у= 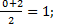 z = z = 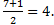 Координаты середины отрезков АС и ВD совпадают, поэтому диагонали АС и ВD четырёхугольника АВСD пересекаются и точкой пересечения делятся пополам, следовательно четырёхугольник АВСD – параллелограмм.
Координаты середины отрезков АС и ВD совпадают, поэтому диагонали АС и ВD четырёхугольника АВСD пересекаются и точкой пересечения делятся пополам, следовательно четырёхугольник АВСD – параллелограмм.
| ||||
| 4. | 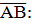 5 – 3 = 2; 1 – (-1) = 2; 1 - 2 = -1. 5 – 3 = 2; 1 – (-1) = 2; 1 - 2 = -1.
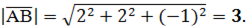
| 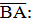 3 – 5 = -2; -1 – 1 = -2; 2 – 1 = 1. 3 – 5 = -2; -1 – 1 = -2; 2 – 1 = 1.
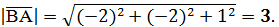
| ||||
| 5. | 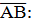 3-1 = 2; -1 – (-1) = 0; 1 – 3 = -2. 3-1 = 2; -1 – (-1) = 0; 1 – 3 = -2.
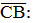 3 – (-1) = 4; -1 – 1 = -2; 1 – 3 = -2. 3 – (-1) = 4; -1 – 1 = -2; 1 – 3 = -2.
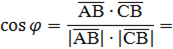
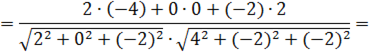
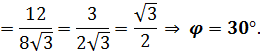
| 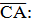 1 – 1 = 0; 3 – 2 = 1; 0 – (-1) = 1. 1 – 1 = 0; 3 – 2 = 1; 0 – (-1) = 1.
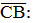 1 – 2 = -1; 3 – 2 = 1; -1 – (-1) = 0. 1 – 2 = -1; 3 – 2 = 1; -1 – (-1) = 0.
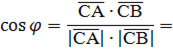
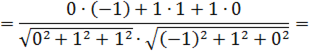
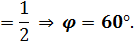
|
Контрольная работа №10.
Вариант 1
1. Дайте определение прямой призмы.
2. Что такое параллелепипед?
3. Что такое многогранник?
4. Задача: У параллелепипеда три грани имеют площади 2 м2, 4 м2 и 5 м2. Чему равна полная поверхность параллелепипеда?
5. Задача: Основание пирамиды – прямоугольник со сторонами 9 и 12 см, все боковые рёбра равны 12,5 м. Найдите объём пирамиды.
Вариант 2
1. Дайте определение правильной призмы.
2. Что такое куб?
3. Чем является точка пересечения диагоналей параллелепипеда?
4. Задача: У параллелепипеда три грани имеют площади 3 м2, 6 м2 и 7 м2. Чему равна полная поверхность параллелепипеда?
5. Задача: Боковые рёбра наклонной треугольной призмы равны 15 м, а расстояния между содержащими их параллельными прямыми 26 м, 25 м и 17 м. Найдите объём призмы.
Вариант 3
1. Дайте определение правильной пирамиды.
2. Какой многогранник называется правильным?
3. Что такое линейные размеры прямоугольного параллелепипеда?
4. Задача: Измерения прямоугольного параллелепипеда 15 м, 50 м и 36 м. Найдите ребро равновеликого ему куба.
5. Задача: Высота правильной четырёхугольной пирамиды равна 7 см, а сторона основания 8 см. Найдите боковое ребро.
Вариант 4
1. Дайте определение апофемы правильной пирамиды.
2. Какой параллелепипед называется прямоугольным?
3. Чему равна боковая поверхность прямой призмы?
4. Задача: Найдите диагонали прямоугольного параллелепипеда по трём его измерениям: 2 см, 3 см, 6 см.
5. Задача: Основание пирамиды – прямоугольник со сторонами 6 см и 8 см. Каждое боковое ребро пирамиды равно 13 см. Вычислите высоту пирамиды.
Ответы к контрольной работе
| № варианта № задания | Вариант 1 | Вариант 2 | Вариант 3 | Вариант 4 | ||||||
| 1. | Призма называется прямой, если её боковые рёбра перпендикулярны основаниям. | Прямая призма на-зывается правиль-ной, если её основа-ния являются пра-вильными много-угольниками. | Пирамида называ-ется правильной, если её основанием является правиль-ный многоуголь-ник, а основание высоты совпадает с центром этого мно-гоугольника. | Высота боковой грани правильной пирамиды, прове-дённая из её верши-ны, называется апофемой. | ||||||
| 2. | Если основания призмы есть параллелограмм, то она называется параллелепипедом. | Прямоугольный параллелепипед, у которого все рёбра равны, называется кубом. | Выпуклый много-гранник называет-ся правильным, ес-ли его грани явля-ются правильными многоугольниками с одним и тем же числом сторон и в каждой вершине многогранника сходится одно и то же число рёбер. | Прямой параллеле-пипед, у которого основанием является прямоугольник, на-зывается прямоугольным параллелепипедом. | ||||||
| 3. | Многогранник – это такое тело, поверх-ность которого сос-тоит из конечного числа плоских мно-гоугольников. | Точка пересечения диагоналей паралле-лепипеда является его центром сим-метрии. | Длины непарал-лельных рёбер пря-моугольного па-раллелепипеда на-зывают его линей-ными размерами. | Боковая поверх-ность прямой приз-мы равна произведе-нию периметра ос-нования на высоту призмы, т.е. на дли-ну бокового ребра. | ||||||
| 4. | Sn=2(2+4+5)= =22 см 2. | Sn=2(3+6+7)= =32 см 2. | Vn= V к
Vn=abc=15∙50∙36
V к =a3 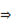 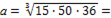
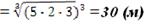
| d2=a2+ b2+ c2=
=22+ 32+ 62=49 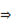 d= d= 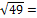 7 (см) 7 (см)
| ||||||
| 5. |
BD= =15(см) О D= SO= = =10( см )
=360 ( см 3 ). |
Sосн.=
Sосн.= . =204 ; V=204∙15=3060(см 3 ) |
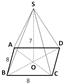 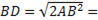 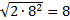 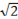 О D=
О D=  BD=4 BD=4 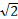
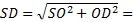
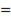 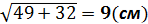
|
О D= SO= = = 12 см. |
Контрольная работа №11.
Объемы и площади.
Вариант 1
1. Дайте определение цилиндра. Нарисуйте цилиндр, укажите его образующую, радиус и осевое сечение.
2. Какой конус называется прямым? Сделать рисунок.
3. Какая плоскость называется диаметральной плоскостью шара? Что такое большой круг? Сделать рисунок.
4. Задача: Куча щебня имеет коническую форму, радиус основания которой 4 м , а образующая 5 м. Найдите объём щебня.
5. Задача: Найти площадь сечения шара радиусом 25 см плоскостью, проведённой на расстоянии 20 см от центра шара.
Вариант 2
1. Дайте определение конуса. Нарисуйте конус, укажите его образующую, радиус, высоту и осевое сечение.
2. Какой цилиндр называется прямым? Сделать рисунок.
3. Какая плоскость называется касательной к шару? Сделать рисунок.
4. Задача: Объём шара равен 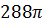 см3. Найдите площадь поверхности шара.
см3. Найдите площадь поверхности шара.
5. Задача: Площадь боковой поверхности конуса равна 15 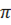 см2, а площадь его основания на 6
см2, а площадь его основания на 6 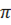 см2 меньше. Найдите объём конуса.
см2 меньше. Найдите объём конуса.
Вариант 3
1. Дайте определение шара. Нарисуйте шар, укажите его центр, радиус.
2. Укажите виды сечений цилиндра и сделайте рисунки.
3. Какая фигура получится при вращении равнобедренного треугольника вокруг его оси симметрии? Сделайте рисунок.
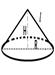
4. Задача: Радиус цилиндра равен 5 см, площадь боковой поверхности вдвое больше площади основания. Найдите объём цилиндра.
5. Задача: Плоскость проходит на расстоянии 6 см от центра шара. Радиус сечения равен 8 см. Найдите площадь поверхности шара.
Вариант 4
1. Почему шар является телом вращения. Сделайте рисунок. Дайте определение сферы.
2. Что такое усечённый конус? Сделать рисунок.
3. Какая фигура получится при вращении прямоугольника вокруг его оси симметрии? Сделайте рисунок.
4. Задача: Площадь осевого сечения цилиндра равна 64 см2. Найдите площадь его боковой поверхности.
5. Задача: Найти объём тела, полученного при вращении прямоугольного треугольника с гипотенузой 24 см и острым углом 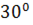 вокруг меньшего катета.
вокруг меньшего катета.
Ответы к контрольной работе
| № варианта № задания | Вариант 1 | Вариант 2 | Вариант 3 | Вариант 4 | ||||||||
| 6. | Цилиндром называется тело, которое состоит из двух кругов (оснований), не лежащих в одной плос-кости и совмещаемых параллельным переносом, и всех отрезков (образующих), соединяю-щих соответствующие точки этих кругов. 
| Конусом называется тело, которое состо-ит из круга –основа- ния конуса, точки, не лежащей в плос-кости этого круга,- вершины конуса и всех отрезков (обра-зующих), соединяю-щих вершину конуса с точками основания 
| Шаром называется тело, которое состоит из всех точек пространства, на-ходящихся на расстоянии, не большем данного, от данной точки. Эта точка называется центром шара, а данное расстояние – радиусом шара. 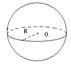
| Шар получается при вра-щении полукруга вокруг
его диаметра как оси.
| ||||||||
| 7. | Конус называется прямым, если прямая, соединяющая вершину конуса с центром основания, перпендикулярна плоскости основания. 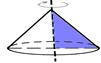
| Цилиндр называется прямым, если его образующие перпендикулярны плоскостям оснований. 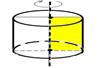
|
сечения параллельные оси и плоскости основания |
от него меньший конус. Оставшаяся часть называется усечённым конусом. | ||||||||
| 8. | Плоскость, проходящая через центр шара, называется диаметральной. 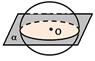
|  Плоскость, проходящая через точ-ку А шаровой поверх-ности и перпендику-лярная радиусу, прове-дённому в точку А, на-зывается касательной плоскостью. Плоскость, проходящая через точ-ку А шаровой поверх-ности и перпендику-лярная радиусу, прове-дённому в точку А, на-зывается касательной плоскостью.
|
|
| ||||||||
| 9. |  
|  Sп= 4πR2 Sп= 4πR2
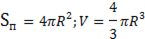
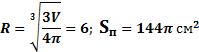
|  V=Sосн.∙Н= πR2H
Sбок.= 2Sосн
2πRH= 2πR2; R=H
V= π52∙5=125π см3 V=Sосн.∙Н= πR2H
Sбок.= 2Sосн
2πRH= 2πR2; R=H
V= π52∙5=125π см3
|
Sбок.=2πRH= = Sос.сеч.π = 64π см2 | ||||||||
| 10. | 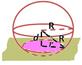 Sсеч= π r 2
r 2 =R 2 - d 2 =
625-400=225
Sсеч= 225π см2 Sсеч= π r 2
r 2 =R 2 - d 2 =
625-400=225
Sсеч= 225π см2
|  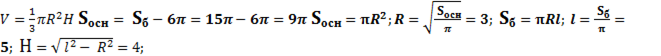 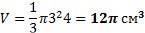
| 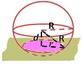 Sп= 4πR2 Sп= 4πR2
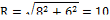 Sп= 4π102=400 π см2
Sп= 4π102=400 π см2
| 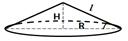
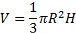 H=l
H=l 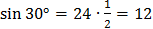
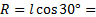
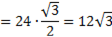
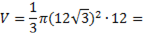 =1728 π см3
=1728 π см3
| ||||||||
Контрольная работа № 12.
Теория вероятностей.
Вариант 1.
1.В парке сажали деревья два года: в 2014 г. 76 деревьев и в 2015 г. 44 деревьев. Какова вероятность того, что произвольно выбранное дерево посажено в 2014 году?
2. Провели несколько измерений случайной величины: 3; 7,6; 2,8; 4; 2; 5,2; 2,8. Найдите моду этого набора чисел.
3. Провели несколько измерений случайной величины: 75; 60; 70; 65; 80; 15; 55.
Найдите среднее арифметической этого набора чисел.
4. Провели несколько измерений случайной величины: 12; 11; 19; 10; 19; 19; 18; 12.
Найдите медиану этого набора.
5.В команде баскетболистов 9 игроков. Их рост в сантиметрах: 200; 200; 200; 180; 180; 189; 210; 180; 180. Найдите сумму медианы и моды этого набора.
6. За диктант по русскому языку учительница поставила 7 пятерок, 9 четверок, 8 троек и 2 двойки. Постройте столбчатую диаграмму по этим данным.
7. В ящике 6 яблок и 9 груш. Наудачу извлекают 3 фрукта. Найти вероятность того, что: а) все фрукты яблоки; б) извлечено 2 яблоко и 1 груша; в) извлечено хотя бы одно яблоко.
8. Электрическая цепь состоит из двух последовательно соединенных элементов. Вероятность безотказной работы первого элемента 0,9, второго 0,7. Какова вероятность, что цепь будет работать, если для работы цепи необходима работа двух элементов?
Вариант 2.
1.В коробке 126 синих и 74 красных шаров. Какова вероятность взять наудачу синий шар?
2. Провели несколько измерений случайной величины: 9; 14; 18; 25; 14; 14; 8; 14; 7; 19.
Найдите моду этого набора чисел.
3. Провели несколько измерений случайной величины: 3400; 2500; 1800; 2200; 3900; 900; 2800; 1600; 1600. Найдите среднее арифметическое этого набора чисел.
4. Провели несколько измерений случайной величины: 95; 145; 100; 120; 155; 90; 120; 115; 145. Найдите медиану этого набора чисел.
5. Посещаемость сайта за 9 месяцев составила следующий ряд: 4500; 4200; 4296; 4300; 4100; 4300; 500; 4400; 4000. Найдите разность моды и медианы этого набора чисел.
6. В фермерском хозяйстве площади, отведенные под посевы зерновых, распределены следующим образом: пшеница- 65%, овес- 18%, просо -10%, гречиха-7%. Построить круговую диаграмму.
7. В ящике 5 новых теннисных мячей и 10 старых теннисных мячей. Наудачу извлекают 3 мяча. Найти вероятность того, что: а) все мячи старые; б) извлечено 2 старых и 1 новый; в) извлечен хотя бы один новый мяч.
8. Электрическая цепь состоит из двух параллельно соединенных элементов. Вероятность безотказной работы первого элемента 0,8, второго 0,7. Какова вероятность, что цепь будет работать, если для работы цепи необходима работа хотя бы одного элемента?
Вариант 3.
1.В лотерее 165 выигрышных билетов и 55 билетов без выигрыша. Какова вероятность получить билет без выигрыша?
2.Провели несколько измерений случайной величины: 2,2; 2,5; 1,9; 1,1; 2,2; 2,1; 2.. Найдите моду этого набора чисел.
3. Провели несколько измерений случайной величины: 34; 66; 54; 62; 66; 28; 16; 44; 48; 62.
Найдите среднее арифметическое этого набора чисел.
4. Провели несколько измерений случайной величины: 2,6; 5; 2; 3,6 ; 3,8; 4,4; 1; 1,2; 4,2; 2,2. Найдите медиану этого набора чисел.
5. Скорость 11 автомобилей, проезжавших через перекресток составила (км/ч):
51; 32; 38; 52; 61; 33; 51; 46; 39; 46; 46. Найдите разность моды и медианы этого набора чисел.
6. За контрольную работу по математике учительница поставила 8 пятерок, 7 четверок, 10 троек и 1 двойка. Постройте столбчатую диаграмму по этим данным.
7. В ящике 5 яблок и 10 груш. Наудачу извлекают 4 фрукта. Найти вероятность того, что: а) все фрукты яблоки; б) извлечено 3 яблоко и 1 груша; в) извлечено хотя бы одно яблоко.
8. Электрическая цепь состоит из двух последовательно соединенных элементов. Вероятность безотказной работы первого элемента 0,6, второго 0,8. Какова вероятность, что цепь будет работать, если для работы цепи необходима работа двух элементов?
Вариант 4.
1.В выпускных классах всего 107 мальчиков и 53 девочек. Какова вероятность, что случайным образом выбранный выпускник окажется мальчиком?
2. Провели несколько измерений случайной величины: 13; 8; 21; 9; 13; 16; 19; 22.
Найдите моду этого набора чисел.
3. Провели несколько измерений случайной величины: 1,2; 1,6; 2,1; 2,3; 2,3; 1; 2; 2,4; 1,1; 2. Найдите среднее арифметическое этого набора чисел.
4. Провели несколько измерений случайной величины: 4,8; 1,6; 3,2; 3,8; 3,8; 1,8; 2,6; 4,2.
Найдите медиану этого набора чисел.
5. Подсчитали объем продаж магазина в течении 10 дней (в тыс. руб.): 41; 33; 33; 45; 35; 37; 33; 29; 25; 39. Найдите разность среднего арифметического и моды этого набора чисел.
6. В фермерском хозяйстве площади, отведенные под посевы зерновых, распределены следующим образом: пшеница- 55%, овес- 23%, просо -13%, гречиха- 9%. Построить круговую диаграмму.
7. В ящике 10 новых теннисных мячей и 10 старых теннисных мячей. Наудачу извлекают 5 мячей. Найти вероятность того, что: а) все мячи старые; б) извлечено 2 старых и 3 новых; в) извлечен хотя бы один новый мяч.
8. Электрическая цепь состоит из двух параллельно соединенных элементов. Вероятность безотказной работы первого элемента 0,9, второго 0,7. Какова вероятность, что цепь будет работать, если для работы цепи необходима работа хотя бы одного элемента?
ТЕСТЫ ПО МАТЕМАТИКЕ
ТЕМА: Интеграл и ее приложение
ВАРИАНТ № 1
| Задание | Вариант ответа |
| 1. Среди заданных функций G ( x ), F ( x ) и H ( x ) выберете первообразную для функции у = -7 х3 | а) G ( x )= -21 х2 б) F ( x )= -7 х4 в) H ( x )= - 7/4 х4 |
| 2. Укажите ту функцию, для которой F ( x )= х3 + 3 x + С имеет общий вид первообразной | а) g ( x )= 3 х2 + 3 б) h ( x )= 3 х2 + 3 x + 9 в) φ( x )= х4/4 + 3 |
| 3. Найдите общий вид первообразных для функции f(x) = 4 sin x + 2 cos x | а) F ( x )= 4 cos x – 2 sin x + С б) F(x)= - 4cos x + 2sin x + С в) F(x)= - 4cos x + 2sin x |
| 4. Найдите общий вид первообразных для функции f ( x ) = 2 sin 3 x | а) F ( x )= - 1/6 cos 3 x + С б) F ( x )= - 2/3 cos x + С в) F ( x )= - 2/3 cos 3 x + С |
| 5. Найдите общий вид первообразных для функции f ( x ) = (2х – 1)5 | а) F ( x )= (2х – 1)6/12 + С б) F ( x )= (2х – 1)6/6 + С в) F ( x )= (2х – 1)6/2 + С |
| 6. Для функции f ( x ) найдите F ( x ), если f ( x ) = 2/ х3 ; F (1)=1 | а) F ( x )= - х-2 - 2 б) F ( x )= - х-2 + 2 в) F ( x )= - 2 х-2 + 3 |
| 7. Верно ли, что на рисунке изображены графики трёх первообразных для некоторой функции? | а) да б) нет |
| 8. Выберете формулу, по которой можно вычислить площадь фигуры, изображённой на рисунке: | в а) S =∫а f ( x ) dx в б) S = - ∫а f ( x ) dx в) S= f( в ) - f( а) |
| 9. Вычислите интеграл 1 ∫ 0 4х3 dx | а) - 1 б) 4 в) 1 |
| 10. По какой формуле нужно находить площадь фигуры, заштрихованной на рисунке: | 2 а) S=∫-1 x2dx 2 б) S=∫0 x2dx -1 в) S=∫2 x2dx |
ВАРИАНТ № 2
| Задание | Вариант ответа |
| 1. Среди заданных функций G ( x ), F ( x ) и H ( x ) выберете первообразную для функции у = 5 х6 | а) G ( x )= 5 х7 б) F ( x )= 30 х5 в) H ( x )= 5х7/7 |
| 2. Укажите ту функцию, для которой F ( x )= х4 - 4х + С имеет общий вид первообразной | а) g ( x )= 4 х3 - 4 + С б) h ( x )= 4 х3 - 4 х2 + 2 в) φ( x )= х5/5 - 2 х2 |
| 3. Найдите общий вид первообразных для функции f(x) = 5 cos x + 2 sin x | а) F(x)= 5 sin x - 2 cos x + С б) F(x)= - 5 sin x - 2 cos x + С в) F ( x )= 5 sin x + 2 cos x + С |
| 4. Найдите общий вид первообразных для функции f ( x ) = 3 cos 2 x | а) F ( x )= - 3/2 sin 2 x + С б) F ( x )= 3/2 sin 2 x + С в) F ( x )= 3/2 sin x + С |
| 5. Найдите общий вид первообразных для функции f ( x ) = (7х – 2)3 | а) F ( x )= (7х – 2)4/4 + С б) F ( x )= 7(7х – 2)4/4 + С в) F ( x )= (7х – 2)4/28 + С |
| 6. Для функции f ( x ) найдите F ( x ), если f ( x ) = 2/ х2 ; F (1)=1 | а) F ( x )= 2 х-1 + 1 б) F ( x )= -2 х-1 + 3 в) F ( x )= 2 х-1 - 1 |
| 7. Верно ли, что на рисунке изображены графики трёх первообразных для некоторой функции? | а) да б) нет |
| 8. Выберете формулу, по которой можно вычислить площадь фигуры, изображённой на рисунке: | в а) S = ∫а f ( x ) dx в б) S = - ∫а f ( x ) dx a в) S = - ∫ в f(x)dx |
| 9. Вычислите интеграл 0 ∫ -1 5х4 dx | а) 5 б) -1 в) 1 |
| 10. По какой формуле нужно находить площадь фигуры, заштрихованной на рисунке: | 1 а) S =∫-2 (х2 +2) dx -2 б) S =∫1(х2 +2) dx 2 в) S =∫-2 (х2 +2) dx |
ВАРИАНТ № 3
| Задание | Вариант ответа |
| 1. Среди заданных функций G ( x ), F ( x ) и H ( x ) выберете первообразную для функции у = -5 х4 | а) G ( x )= -20 х3 б) F ( x )= - х5 в) H ( x )= - 5/4 х5 |
| 2. Укажите ту функцию, для которой F ( x )= х2 - 2 x + С имеет общий вид первообразной | а) g ( x )= 2х - 2 б) h ( x )= 2 х3 - 2 x 2 + 2 в) φ( x )= х3/3 - 2 |
| 3. Найдите общий вид первообразных для функции f(x) = 6 sin x + 3 cos x | а) F ( x )= 6 cos x – 3 sin x + С б) F(x)= - 6 cos x + 3 sin x в) F ( x )= - 6 cos x + 3 sin x + С |
| 4. Найдите общий вид первообразных для функции f ( x ) = 5 sin 4 x | а) F ( x )= 1/4 cos 5 x + С б) F ( x )= - 5/4 cos x + С в) F ( x )= - 5/4 cos 4 x + С |
| 5. Найдите общий вид первообразных для функции f ( x ) = (1 - 5х)3 | а) F ( x )= -(1 - 5х)4/20 + С б) F ( x )= (1 - 5х)4/4 + С в) F ( x )= (1 - 2х)3/3 + С |
| 6. Для функции f ( x ) найдите F ( x ), если f ( x ) = 4/ х5 ; F (1)=1 | а) F ( x )= - х-4 - 2 б) F ( x )= - х-4 + 2 в) F ( x )= 6 х-6 + 3 |
| 7. Верно ли, что на рисунке изображены графики трёх первообразных для некоторой функции? | а) да б) нет |
| 8. Выберете формулу, по которой можно вычислить площадь фигуры, изображённой на рисунке: | в а) S =-∫а f ( x ) dx в б) S = ∫а f ( x ) dx в) S = f (а) - f (в) |
| 9. Вычислите интеграл 1 ∫ 0 6х5 dx | а) 6 б) -1 в) 1 |
| 10. По какой формуле нужно находить площадь фигуры, заштрихованной на рисунке: | 1 а) S=∫-1 (x2 -1)dx 1 б) S=∫0 (x2 -1)dx -1 в) S=∫ 1 (x2 -1 ) dx |
ВАРИАНТ № 4
| Задание | Вариант ответа |
| 1. Среди заданных функций G ( x ), F ( x ) и H ( x ) выберете первообразную для функции у = 9 х8 | а) G ( x )= х9 б) F ( x )= 72 х7 в) H ( x )= 9 х7/7 |
| 2. Укажите ту функцию, для которой F ( x )= х5 - 5х + С имеет общий вид первообразной | а) g ( x )= 5 х4 - 5 х2 + С б) h ( x )= 5 х6 - 5 х2 в) φ( x )= 5х4 - 5 |
| 3. Найдите общий вид первообразных для функции f(x) = 4 cos x + 7 sin x | а) F(x)= 4 sin x - 7 cos x + С б) F(x)= - 4 sin x - 7 cos x + С в) F ( x )= 4 sin x + 7 cos x + С |
| 4. Найдите общий вид первообразных для функции f ( x ) = 9 cos 3 x | а) F ( x )= - 3 sin 3 x + С б) F ( x )= 3 sin 3 x + С в) F ( x )= 3 sin x + С |
| 5. Найдите общий вид первообразных для функции f ( x ) = (7х – 2)3 | а) F ( x )= (7х – 2)4/4 + С б) F ( x )= 7(7х – 2)4/4 + С в) F ( x )= (7х – 2)4/28 + С |
| 6. Для функции f ( x ) найдите F ( x ), если f ( x ) = 5/ х6 ; F (1)=1 | а) F ( x )= х-5 + 1 б) F ( x )= - х-5 + 2 в) F ( x )= - х-5 - 1 |
| 7. Верно ли, что на рисунке изображены графики трёх первообразных для некоторой функции? | а) да б) нет |
| 8. Выберете формулу, по которой можно вычислить площадь фигуры, изображённой на рисунке: | в а) S = ∫а f ( x ) dx в б) S = - ∫а f ( x ) dx a в) S = - ∫ в f(x)dx |
| 9. Вычислите интеграл 0 ∫ -1 7х6 dx | а) 7 б) -1 в) 1 |
| 10. По какой формуле нужно находить площадь фигуры, заштрихованной на рисунке: | 3 а) S =∫0 (х -1)2 dx 3 б) S =∫1(х -1)2 dx 1 в) S =∫3 (х -1)2 dx |
Ключ к тесту
« ПЕРВООБАЗНАЯ И ИНТЕГРАЛ»:
ВАРИАНТ № 1: в, а, б, в, а, б, а, а, в, а.
ВАРИАНТ № 2: в, а, а, б, в, б, б, б, в, а.
ВАРИАНТ № 3: б, а, в, в, а, б, б, а, в, а
ВАРИАНТ № 4: а, в, а, б, в, б, а, а, в, б.
ВАРИАНТ № 1
| Задание | Вариант ответа |
| 1. Продолжи предложение: Стереометрия – это раздел геометрии, в котором изучаются фигуры…. | а) на плоскости; б) в пространстве; в) на прямой. |
| 2. Какие прямые в пространстве называются параллельными? | а) если ни лежат в одной плоскости и не пересекаются; б) если они лежат в одной плоскости и пересекаются; в) если они лежат в разных плоскостях и не пересекаются. |
| 3. На рис.1 скрещивающимися являются прямые: | а) АВ и ВВ1; б) АВ и Д1С1; в) АВ и А1Д1. |
4. Записать, используя математическую символику:
 Плоскость α пересекает плоскость β по прямой а. Плоскость α пересекает плоскость β по прямой а.
| а) α β= а; б) α∩β= а; в) α Є β= а. |
| 5. Как прочесть запись: [АВ] а; а Є α ? | а) отрезок АВ принадлежит прямой а, не лежащей в плоскости α; б) отрезок АВ лежит на прямой а, не принадлежащей плоскости α; в) точки А и В лежат на прямой а, не принадлежащей плоскости α; |
| 6. Точки А, В, С и Д не лежат в одной плоскости | а) прямые АВ и СД пересекаются; б) прямые АВ и СД не пересекаются. |
| 7. Прямые АВ и СД не лежат в одной плоскости | а) прямые АС и ВД не лежат в одной плоскости; б) прямые АС и ВД лежат в одной плоскости; |
| 8. Может ли при параллельном проектировании параллелограмма получиться трапеция? | а) может, так как при параллельном проектировании параллельность не сохраняется; б) не может, так как при параллельном проектировании параллельность сохраняется. |
| 9. Через точки А, В и середину М отрезка АВ проведены параллельные прямые, пересекающие некоторую плоскость α в точках А1, В1, М1 соответственно. Найти отрезок М1М1, если А А1=3м; ВВ1=17м, причем АВ не пересекает плоскость α. | а) М1М1=10 м; б) М1М1=62/3 м; в) М1М1=20м. |
| 10.Дано: ∆АВС; α||АВ; АС∩ α= А1; ВС∩ α= В1; АВ=15 см; АА1: АС=2:3. Найти А1В1 -? | а) А1В1=45 см; б) А1В1= 5 см; в) А1В1=10 см. |
ВАРИАНТ № 2
| Задание | Вариант ответа |
| 2. Продолжи предложение: Основными фигурами в пространстве являются…. | а) точка и прямая; б) точка и плоскость; в) точка, прямая и плоскость. |
| 2. Какие прямые называются скрещивающимися? | а) прямые, которые не пересекаются и не лежат в одной плоскости; б) прямые, которые пересекаются и лежат в одной плоскости; в) прямые, которые не пересекаются и лежат в одной плоскости. |
| 3. На рис.1 параллельными являются прямые: | а) А1А и ВС; б) А1 Д1 и ВС; в) А1 В1 и ВС1. |
| 4. Записать, используя математическую символику: Прямая а пересекает плоскость α в точке А . | а) а α= А; б) а α= А; в) а∩α= А. |
| 5. Как прочесть запись: {А;В} Є а; а α ? | а) отрезок АВ принадлежит прямой а, лежащей в плоскости α; б) точки А и В принадлежат прямой а, которая лежит в плоскости α; в) точки А и В лежат на прямой а, не принадлежащей плоскости α; |
| 6. Могут ли прямые а и в пересекаться? с||в. | а) нет; б) могут. |
| 7. Четыре точки не лежат в одной плоскости. Могут ли какие-нибудь три из них лежать на одной прямой? | а)могут; б) не могут. |
| 8. Может ли проекция параллелограмма при параллельном проектировании быть квадратом? | а) может, так как при параллельном проектировании параллельность сохраняется; б) не может, так как при параллельном проектировании параллельность не сохраняется. |
| 9. Через точки А, В и середину М отрезка АВ проведены параллельные прямые, пересекающие некоторую плоскость α в точках А1, В1, М1 соответственно. Найти отрезок М1М1, если А А1=13м; ВВ1=7м, причем АВ не пересекает плоскость α. | а) М1М1=21/7 м; б) М1М1=20 м; в) М1М1=10м. |
| 10.Дано: ∆АВС; α||АВ; АС∩ α= А1; ВС∩ α= В1; АВ=8 см; АА1: АС=5:3. Найти А1В1 -? | а) А1В1=1 см; б) А1В1= 3 см; в) А1В1=4 см. |
ВАРИАНТ № 3
| Задание | Вариант ответа |
| 3. Продолжи предложение: В стереометрии свойства геометрических фигур устанавливаются путём доказательства соответствующих…. | а) аксиом; б) теорем; в) задач. |
| 2. Что значит: прямая и плоскость параллельны? | а) прямая и плоскость не пересекаются; б) прямая и плоскость пересекаются и лежат в одной плоскости; в) прямая и плоскость не пересекаются, то есть не имеют общих точек. |
| 3. На рис.1 скрещивающимися являются прямые: | а) А1А и ВС; б) А1 Д1 и ВС; в) А1 В1 и АВ. |
| 4. Записать, используя математическую символику: Плоскость α пересекает плоскость β по прямой с. | а) α β = с; б) α β = с; в) α ∩ β = с. |
| 5. Как прочесть запись: [ВС] Єс; с α ? | а) отрезок ВС принадлежит прямой с, лежащей в плоскости α; б) точки С и В принадлежат прямой с, которая лежит в плоскости α; в) точки А и В лежат на прямой с, не принадлежащей плоскости α; |
| 6. Точки К, L, M и N не лежат в одной плоскости | а) прямые KL и MN пересекаются; б) прямые KL и MN не пересекаются. |
| 7.Плоскости α и β параллельны плоскости γ. Могут ли плоскости α и β пересекаться? | а) могут; б) не могут. |
| 8.Дана параллельная проекция треугольника. Чем изображается проекция средней линии треугольника? | а) средней линией, так как при параллельном проектировании сохраняется отношение отрезков; б) средней линией, так как при параллельном проектировании не сохраняется отношение отрезков . |
| 9. Через точки А, В и середину М отрезка АВ проведены параллельные прямые, пересекающие некоторую плоскость α в точках А1, В1, М1 соответственно. Найти отрезок М1М1, если А А1=25дм; ВВ1=5дм, причем АВ не пересекает плоскость α. | а) М1М1=5 дм; б) М1М1=30 дм; в) М1М1=15 дм. |
| 10.Дано: ∆АВС; α||АВ; АС∩ α= А1; ВС∩ α= В1; АВ=24 см; АА1: АС=5:1. Найти А1В1 -? | а) А1В1=6 см; б) А1В1= 3 см; в) А1В1=4 см. |
Ключ к тесту
по теме:
«Аксиомы стереометрии и их простейшие следствия. Параллельность прямых и плоскостей»:
ВАРИАНТ № 1: б, а, в, б, б, б, а, б, а, б
ВАРИАНТ № 2: в, а, б, в, б, а, б, а, в, б.
ВАРИАНТ № 3: б, в, а, в, а, б, б, а, в, в.
Пакет для экзаменатора
Форма промежуточной аттестации – экзамен. Для его проведения подготовлены экзаменационные тестовые задания и экзаменационные билеты. Выбор вида экзаменационной работы (тесты или билеты) осуществляют обучающиеся.
В результате оценки осуществляется проверка следующих объектов:
Базовый уровень
Алгебра и начала анализа
Повторение. Решение задач с использованием свойств чисел, делимости, долей и частей, процентов, модулей чисел. Решение задач с использованием свойств степеней и корней, многочленов, преобразований многочленов и дробно-рациональных выражений.
Решение задач с использованием градусной меры угла. Модуль числа и его свойства.
Решение задач на движение и совместную работу с помощью линейных и квадратных уравнений и их систем. Решение задач с помощью числовых неравенств и систем неравенств с одной переменной, с применением изображения числовых промежутков.
Решение задач с использованием числовых функций и их графиков. Использование свойств и графиков линейных и квадратичных функций, обратной пропорциональности и функции 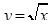 . Графическое решение уравнений и неравенств.
. Графическое решение уравнений и неравенств.
Тригонометрическая окружность, радианная мера угла. Синус, косинус, тангенс, котангенс произвольного угла. Основное тригонометрическое тождество и следствия из него. Значения тригонометрических функций для углов 0°, 30°, 45°, 60°, 90°, 180°, 270°. ( 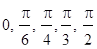 рад). Формулы сложения тригонометрических функций, формулы приведения, формулы двойного аргумента.
рад). Формулы сложения тригонометрических функций, формулы приведения, формулы двойного аргумента.
Нули функции, промежутки знакопостоянства, монотонность. Наибольшее и наименьшее значение функции. Периодические функции. Четность и нечетность функций. Сложные функции.
Тригонометрические функции 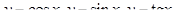 ,
, 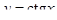 . Свойства и графики тригонометрических функций.
. Свойства и графики тригонометрических функций.
Арккосинус, арксинус, арктангенс числа. Арккотангенс числа. Простейшие тригонометрические уравнения. Решение тригонометрических уравнений.
Обратные тригонометрические функции, их свойства и графики. Решение простейших тригонометрических неравенств.
Степень с действительным показателем, свойства степени. Простейшие показательные уравнения и неравенства. Показательная функция и ее свойства и график.
Логарифм числа, свойства логарифма. Десятичный логарифм. Число е. Натуральный логарифм. Преобразование логарифмических выражений. Логарифмические уравнения и неравенства. Логарифмическая функция и ее свойства и график.
Степенная функция и ее свойства и график. Иррациональные уравнения.
Метод интервалов для решения неравенств.
Преобразования графиков функций: сдвиг вдоль координатных осей, растяжение и сжатие, отражение относительно координатных осей. Графические методы решения уравнений и неравенств. Решение уравнений и неравенств, содержащих переменную под знаком модуля.
Системы показательных, логарифмических и иррациональных уравнений. Системы показательных, логарифмических неравенств.
Взаимно обратные функции. Графики взаимно обратных функций.
Уравнения, системы уравнений с параметром.
Производная функции в точке. Касательная к графику функции. Геометрический и физический смысл производной. Производные элементарных функций. Правила дифференцирования.
Вторая производная, ее геометрический и физический смысл.
Понятие о непрерывных функциях. Точки экстремума (максимума и минимума). Исследование элементарных функций на точки экстремума, наибольшее и наименьшее значение с помощью производной. Построение графиков функций с помощью производных. Применение производной при решении задач.
Первообразная. Первообразные элементарных функций. Площадь криволинейной трапеции. Формула Ньютона-Лейбница. Определенный интеграл. Вычисление площадей плоских фигур и объемов тел вращения с помощью интеграла.
Геометрия
Повторение. Решение задач с применением свойств фигур на плоскости. Задачи на доказательство и построение контрпримеров. Использование в задачах простейших логических правил. Решение задач с использованием теорем о треугольниках, соотношений в прямоугольных треугольниках, фактов, связанных с четырехугольниками. Решение задач с использованием фактов, связанных с окружностями. Решение задач на измерения на плоскости, вычисление длин и площадей. Решение задач с помощью векторов и координат.
Наглядная стереометрия. Фигуры и их изображения (куб, пирамида, призма). Основные понятия стереометрии и их свойства. Сечения куба и тетраэдра.
Точка, прямая и плоскость в пространстве, аксиомы стереометрии и следствия из них. Взаимное расположение прямых и плоскостей в пространстве. Параллельность прямых и плоскостей в пространстве. Изображение простейших пространственных фигур на плоскости.
Расстояния между фигурами в пространстве.
Углы в пространстве. Перпендикулярность прямых и плоскостей.
Проекция фигуры на плоскость. Признаки перпендикулярности прямых и плоскостей в пространстве. Теорема о трех перпендикулярах.
Многогранники. Параллелепипед. Свойства прямоугольного параллелепипеда. Теорема Пифагора в пространстве. Призма и пирамида. Правильная пирамида и правильная призма. Прямая пирамида. Элементы призмы и пирамиды.
Тела вращения: цилиндр, конус, сфера и шар. Основные свойства прямого кругового цилиндра, прямого кругового конуса. Изображение тел вращения на плоскости.
Представление об усеченном конусе, сечения конуса (параллельное основанию и проходящее через вершину), сечения цилиндра (параллельно и перпендикулярно оси), сечения шара. Развертка цилиндра и конуса.
Простейшие комбинации многогранников и тел вращения между собой. Вычисление элементов пространственных фигур (ребра, диагонали, углы).
Площадь поверхности правильной пирамиды и прямой призмы. Площадь поверхности прямого кругового цилиндра, прямого кругового конуса и шара.
Понятие об объеме. Объем пирамиды и конуса, призмы и цилиндра. Объем шара.
Подобные тела в пространстве. Соотношения между площадями поверхностей и объемами подобных тел.
Движения в пространстве: параллельный перенос, центральная симметрия, симметрия относительно плоскости, поворот. Свойства движений. Применение движений при решении задач.
Векторы и координаты в пространстве. Сумма векторов, умножение вектора на число, угол между векторами. Коллинеарные и компланарные векторы. Скалярное произведение векторов. Теорема о разложении вектора по трем некомпланарным векторам. Скалярное произведение векторов в координатах. Применение векторов при решении задач на нахождение расстояний, длин, площадей и объемов.
Уравнение плоскости в пространстве. Уравнение сферы в пространстве. Формула для вычисления расстояния между точками в пространстве.
Вероятность и статистика. Работа с данными
Повторение. Решение задач на табличное и графическое представление данных. Использование свойств и характеристик числовых наборов: средних, наибольшего и наименьшего значения, размаха, дисперсии. Решение задач на определение частоты и вероятности событий. Вычисление вероятностей в опытах с равновозможными элементарными исходами. Решение задач с применением комбинаторики. Решение задач на вычисление вероятностей независимых событий, применение формулы сложения вероятностей. Условная вероятность. Правило умножения вероятностей. Формула полной вероятности.
Дискретные случайные величины и распределения. Независимые случайные величины. Распределение суммы и произведения независимых случайных величин.
Математическое ожидание и дисперсия случайной величины. Математическое ожидание и дисперсия суммы случайных величин. Геометрическое распределение. Биномиальное распределение и его свойства.
Непрерывные случайные величины. Понятие о плотности вероятности. Равномерное распределение.
Показательное распределение, его параметры.
Понятие о нормальном распределении. Параметры нормального распределения. Примеры случайных величин, подчиненных нормальному закону (погрешность измерений, рост человека).
Углубленный уровень
Алгебра и начала анализа
Повторение. Решение задач с использованием свойств чисел и систем счисления, делимости, долей и частей, процентов, модулей чисел. Решение задач с использованием свойств степеней и корней, многочленов, преобразований многочленов и дробно-рациональных выражений. Решение задач с использованием градусной меры угла. Модуль числа и его свойства. Решение задач на движение и совместную работу, смеси и сплавы с помощью линейных, квадратных и дробно-рациональных уравнений и их систем. Решение задач с помощью числовых неравенств и систем неравенств с одной переменной, с применением изображения числовых промежутков. Решение задач с использованием числовых функций и их графиков. Использование свойств и графиков линейных и квадратичных функций, обратной пропорциональности и функции. Графическое решение уравнений и неравенств. Использование операций над множествами и высказываниями. Использование неравенств и систем неравенств с одной переменной, числовых промежутков, их объединений и пересечений. Применение при решении задач свойств арифметической и геометрической прогрессии, суммирования бесконечной сходящейся геометрической прогрессии.
Множества (числовые, геометрических фигур). Характеристическое свойство, элемент множества, пустое, конечное, бесконечное множество. Способы задания множеств Подмножество. Отношения принадлежности, включения, равенства. Операции над множествами. Круги Эйлера. Конечные и бесконечные, счетные и несчетные множества.
Истинные и ложные высказывания, операции над высказываниями. Алгебра высказываний. Связь высказываний с множествами. Кванторы существования и всеобщности.
Законы логики. Основные логические правила. Решение логических задач с использованием кругов Эйлера, основных логических правил.
Умозаключения. Обоснования и доказательство в математике. Теоремы. Виды математических утверждений. Виды доказательств. Математическая индукция. Утверждения: обратное данному, противоположное, обратное противоположному данному. Признак и свойство, необходимые и достаточные условия.
Радианная мера угла, тригонометрическая окружность. Тригонометрические функции чисел и углов. Формулы приведения, сложения тригонометрических функций, формулы двойного и половинного аргумента. Преобразование суммы, разности в произведение тригонометрических функций, и наоборот.
Нули функции, промежутки знакопостоянства, монотонность. Наибольшее и наименьшее значение функции. Периодические функции и наименьший период. Четные и нечетные функции. Функции «дробная часть числа» и «целая часть числа».
Тригонометрические функции числового аргумента. Свойства и графики тригонометрических функций.
Обратные тригонометрические функции, их главные значения, свойства и графики. Тригонометрические уравнения. Однородные тригонометрические уравнения. Решение простейших тригонометрических неравенств. Простейшие системы тригонометрических уравнений.
Степень с действительным показателем, свойства степени. Простейшие показательные уравнения и неравенства. Показательная функция и ее свойства и график. Число и функция.
Логарифм, свойства логарифма. Десятичный и натуральный логарифм. Преобразование логарифмических выражений. Логарифмические уравнения и неравенства. Логарифмическая функция и ее свойства и график.
Степенная функция и ее свойства и график. Иррациональные уравнения.
Первичные представления о множестве комплексных чисел. Действия с комплексными числами. Комплексно сопряженные числа. Модуль и аргумент числа. Тригонометрическая форма комплексного числа. Решение уравнений в комплексных числах.
Метод интервалов для решения неравенств. Преобразования графиков функций: сдвиг, умножение на число, отражение относительно координатных осей. Графические методы решения уравнений и неравенств. Решение уравнений и неравенств, содержащих переменную под знаком модуля.
Системы показательных, логарифмических и иррациональных уравнений. Системы показательных, логарифмических и иррациональных неравенств.
Взаимно обратные функции. Графики взаимно обратных функций.
Уравнения, системы уравнений с параметром.
Формула Бинома Ньютона. Решение уравнений степени выше 2 специальных видов. Теорема Виета, теорема Безу. Приводимые и неприводимые многочлены. Основная теорема алгебры. Симметрические многочлены. Целочисленные и целозначные многочлены.
Суммы и ряды, методы суммирования и признаки сходимости.
Теоремы о приближении действительных чисел рациональными.
Множества на координатной плоскости.
Понятие предела функции в точке. Понятие предела функции в бесконечности. Асимптоты графика функции. Сравнение бесконечно малых и бесконечно больших. Непрерывность функции. Свойства непрерывных функций.
Дифференцируемость функции. Производная функции в точке. Касательная к графику функции. Геометрический и физический смысл производной. Применение производной в физике. Производные элементарных функций. Правила дифференцирования.
Вторая производная, ее геометрический и физический смысл.
Точки экстремума (максимума и минимума). Исследование элементарных функций на точки экстремума, наибольшее и наименьшее значение с помощью производной. Построение графиков функций с помощью производных. Применение производной при решении задач. Нахождение экстремумов функций нескольких переменных.
Первообразная. Неопределенный интеграл. Первообразные элементарных функций. Площадь криволинейной трапеции. Формула Ньютона-Лейбница. Определенный интеграл. Вычисление площадей плоских фигур и объемов тел вращения с помощью интеграла.
Методы решения функциональных уравнений и неравенств.
Геометрия
Повторение. Решение задач с использованием свойств фигур на плоскости. Решение задач на доказательство и построение контрпримеров. Применение простейших логических правил. Решение задач с использованием теорем о треугольниках, соотношений в прямоугольных треугольниках, фактов, связанных с четырехугольниками. Решение задач с использованием фактов, связанных с окружностями. Решение задач на измерения на плоскости, вычисления длин и площадей. Решение задач с помощью векторов и координат.
Наглядная стереометрия. Призма, параллелепипед, пирамида, тетраэдр.
Основные понятия геометрии в пространстве. Аксиомы стереометрии и следствия из них. Понятие об аксиоматическом методе.
Теорема Менелая для тетраэдра. Построение сечений многогранников методом следов. Центральное проектирование. Построение сечений многогранников методом проекций.
Скрещивающиеся прямые в пространстве. Угол между ними. Методы нахождения расстояний между скрещивающимися прямыми.
Теоремы о параллельности прямых и плоскостей в пространстве. Параллельное проектирование и изображение фигур. Геометрические места точек в пространстве.
Перпендикулярность прямой и плоскости. Ортогональное проектирование. Наклонные и проекции. Теорема о трех перпендикулярах.
Виды тетраэдров. Ортоцентрический тетраэдр, каркасный тетраэдр, равногранный тетраэдр. Прямоугольный тетраэдр. Медианы и бимедианы тетраэдра.
Достраивание тетраэдра до параллелепипеда.
Расстояния между фигурами в пространстве. Общий перпендикуляр двух скрещивающихся прямых.
Углы в пространстве. Перпендикулярные плоскости. Площадь ортогональной проекции. Перпендикулярное сечение призмы. Трехгранный и многогранный угол. Свойства плоских углов многогранного угла. Свойства плоских и двугранных углов трехгранного угла. Теоремы косинусов и синусов для трехгранного угла.
Виды многогранников. Развертки многогранника. Кратчайшие пути на поверхности многогранника.
Теорема Эйлера. Правильные многогранники. Двойственность правильных многогранников.
Призма. Параллелепипед. Свойства параллелепипеда. Прямоугольный параллелепипед. Наклонные призмы.
Пирамида. Виды пирамид. Элементы правильной пирамиды. Пирамиды с равнонаклоненными ребрами и гранями, их основные свойства.
Площади поверхностей многогранников.
Тела вращения: цилиндр, конус, шар и сфера. Сечения цилиндра, конуса и шара. Шаровой сегмент, шаровой слой, шаровой сектор (конус).
Усеченная пирамида и усеченный конус.
Элементы сферической геометрии. Конические сечения.
Касательные прямые и плоскости. Вписанные и описанные сферы. Касающиеся сферы. Комбинации тел вращения.
Векторы и координаты. Сумма векторов, умножение вектора на число. Угол между векторами. Скалярное произведение.
Уравнение плоскости. Формула расстояния между точками. Уравнение сферы. Формула расстояния от точки до плоскости. Способы задания прямой уравнениями.
Решение задач и доказательство теорем с помощью векторов и методом координат. Элементы геометрии масс.
Понятие объема. Объемы многогранников. Объемы тел вращения. Аксиомы объема. Вывод формул объемов прямоугольного параллелепипеда, призмы и пирамиды. Формулы для нахождения объема тетраэдра. Теоремы об отношениях объемов.
Приложения интеграла к вычислению объемов и поверхностей тел вращения. Площадь сферического пояса. Объем шарового слоя. Применение объемов при решении задач.
Площадь сферы.
Развертка цилиндра и конуса. Площадь поверхности цилиндра и конуса.
Комбинации многогранников и тел вращения.
Подобие в пространстве. Отношение объемов и площадей поверхностей подобных фигур.
Движения в пространстве: параллельный перенос, симметрия относительно плоскости, центральная симметрия, поворот относительно прямой.
Преобразование подобия, гомотетия. Решение задач на плоскости с использованием стереометрических методов.
Вероятность и статистика, логика, теория графов и комбинаторика
Повторение. Использование таблиц и диаграмм для представления данных. Решение задач на применение описательных характеристик числовых наборов: средних, наибольшего и наименьшего значения, размаха, дисперсии и стандартного отклонения. Вычисление частот и вероятностей событий. Вычисление вероятностей в опытах с равновозможными элементарными исходами. Использование комбинаторики. Вычисление вероятностей независимых событий. Использование формулы сложения вероятностей, диаграмм Эйлера, дерева вероятностей, формулы Бернулли.
Вероятностное пространство. Аксиомы теории вероятностей.
Условная вероятность. Правило умножения вероятностей. Формула полной вероятности. Формула Байеса.
Дискретные случайные величины и распределения. Совместные распределения. Распределение суммы и произведения независимых случайных величин. Математическое ожидание и дисперсия случайной величины. Математическое ожидание и дисперсия суммы случайных величин.
Бинарная случайная величина, распределение Бернулли. Геометрическое распределение. Биномиальное распределение и его свойства.
Непрерывные случайные величины. Плотность вероятности. Функция распределения. Равномерное распределение.
Показательное распределение, его параметры.
Распределение Пуассона и его применение. Нормальное распределение. Функция Лапласа. Параметры нормального распределения. Примеры случайных величин, подчиненных нормальному закону (погрешность измерений, рост человека). Центральная предельная теорема.
Неравенство Чебышева. Теорема Чебышева и теорема Бернулли. Закон больших чисел. Выборочный метод измерения вероятностей. Роль закона больших чисел в науке, природе и обществе.
Ковариация двух случайных величин. Понятие о коэффициенте корреляции. Совместные наблюдения двух случайных величин. Выборочный коэффициент корреляции. Линейная регрессия.
Статистическая гипотеза. Статистика критерия и ее уровень значимости. Проверка простейших гипотез. Эмпирические распределения и их связь с теоретическими распределениями. Ранговая корреляция
Экзаменационные билеты
Условием положительной аттестации дисциплины является положительная оценка освоения всех умений и знаний по всем контролируемым показателям
Экзаменационные тестовые задания
Подготовлены 3 варианта тестовых заданий. Для контроля знаний по УД студентам в каждом варианте предлагаются 45 заданий. Задания позволяют оценить знания фактов, исторической терминологии, умения выявлять связи данного явления с другими явлениями, определять главные подходы к изучению исторических явлений.
По степени сложности задания распределены следующим образом. 60% заданий - на 1 и 2 уровне (они соответствуют первому (“фактическому “) уровню знаний), 30% на III уровне – операционном (он заключается в умении осуществлять простейшие логические операции по готовому образцу), 10 на IV уровне - аналитико-синтетическом (проявляются умение обобщать, дифференцировать устойчивые знания)
38 тестовых заданий закрытой формы (с выбором правильного ответа),
2 задания на соответствие (выявление ассоциативных связей)
Пакет для экзаменующихся
| ||||||||
ЭКЗАМЕНАЦИОННЫЕ БИЛЕТЫ
ПО УЧЕБНОЙ ДИСЦИПЛИНЕ «МАТЕМАТИКА»
КУРС
2018
| Рассмотрено на заседании ЦК гуманитарных и естественнонаучных дисциплин Протокол № _________________ Председатель ЦК _________ Е.Н.Гармаева | Утверждаю зам.директора по УВиМР Димова И.Н. _____________ |
Составитель Жаргалсайхан З, Бадмацыренова С.Б. - преподаватели математики ТЭТ
Критерии оценки:
Оценка «отлично» выставляется студенту, если тема раскрыта им в полной мере, приведены примеры, доказаны теоремы, решены все задания. Студент должен проявить знание математических формул.
Оценка «хорошо» выставляется студенту, если тема раскрыта в достаточной мере, но при этом какой-либо важный аспект темы освещен им поверхностно; решены все задания, приведены примеры.
Оценка «удовлетворительно» выставляется студенту, если тема раскрыта в достаточной мере, но при этом какой-либо важный аспект темы освещен им поверхностно; решены не все задания, приведены примеры.
Оценка «неудовлетворительно» выставляется студенту, если тема не раскрыта в достаточной мере, не решены задания, не приведены примеры.
Обязательная часть
Дополнительная часть
ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ №1
Обязательная часть
Дополнительная часть
ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ №2
Обязательная часть
Дополнительная часть
ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ №3
Обязательная часть
Дополнительная часть
ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ №4
Обязательная часть
Дополнительная часть
ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ №5
Обязательная часть
Дополнительная часть
ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ №6
Обязательная часть
Дополнительная часть
ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ №7
Обязательная часть
Дополнительная часть
ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ №8
Обязательная часть
Дополнительная часть
ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ №9
Обязательная часть
Дополнительная часть
ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ №10
Обязательная часть
Дополнительная часть
ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ №11
Обязательная часть
Дополнительная часть
ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ №12
Обязательная часть
Дополнительная часть
ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ №13
Обязательная часть
Дополнительная часть
ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ №14
Обязательная часть
Дополнительная часть
ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ №15
Обязательная часть
Дополнительная часть
ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ №16
Обязательная часть
Дополнительная часть
ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ №17
Обязательная часть
Дополнительная часть
ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ №18
Обязательная часть
Дополнительная часть
ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ №19
Обязательная часть
Дополнительная часть
ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ №20
Обязательная часть
Дополнительная часть
ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ №21
Обязательная часть
Дополнительная часть
ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ №22
Обязательная часть
Дополнительная часть
ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ №23
Обязательная часть
Дополнительная часть
ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ №24
Обязательная часть
Дополнительная часть
ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ №25
Обязательная часть
Дополнительная часть
ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ №26
Обязательная часть
Дополнительная часть
ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ №27
Обязательная часть
Дополнительная часть
ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ №28
Обязательная часть
Дополнительная часть
ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ №29
Обязательная часть
Дополнительная часть
ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ №30
Обязательная часть
Дополнительная часть
Бурятский респотребсоюз

КОМПЛЕКТ КОНТРОЛЬНО-ОЦЕНОЧНЫХ СРЕДСТВ
Дата: 2018-12-21, просмотров: 812.

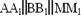
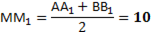
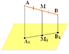
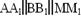
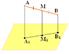
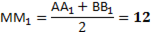
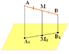
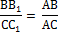
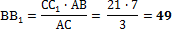
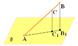
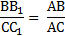
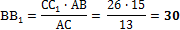
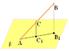
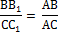
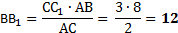
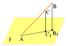
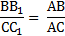
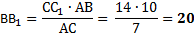
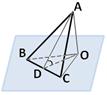
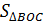 =
= 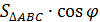
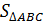 =
= 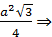
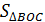 =
= 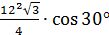 =
= 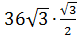 =54(см2)
=54(см2)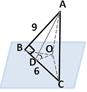
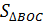 =
= 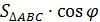
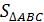 =
= 
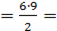 27
27
 13,5(см2)
13,5(см2)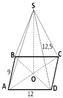
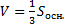 H
Sосн. =
=9•12=
= 108см2
H
Sосн. =
=9•12=
= 108см2
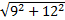 =
= 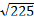 =
=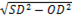 =
=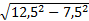 =
= 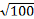 =
=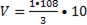 =
=
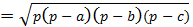
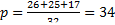 ;
;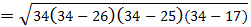 =
=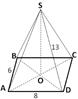
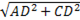 =
=10 (см)
=
=10 (см)
 BD= 5 см
BD= 5 см 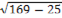 =
= 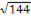 =
=