Вариант 1
1. Вычислить arccos(- 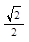 ) - arcsin
) - arcsin 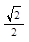 .
.
2. Решить неравенство tg х ≤ -1.
3. Решить уравнения
а) tg 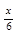 =0;
=0;
б) sin 2 х - 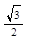 sin х=0;
sin х=0;
в) cos 2 х + cos х – 2 =0.
Вариант 2
1. Вычислить arctg (- 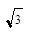 ) - arcsin
) - arcsin 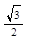 .
.
2. Решить неравенство cos х < 0.
3. Решить уравнения
а) cos (х - 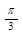 ) =
) = 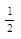 ;
;
б) tg 2 х - tg х=0;
в) sin 2 х + sin х – 2 =0.
Контрольная работа №5
ПРОИЗВОДНАЯ И ЕЁ ПРИЛОЖЕНИЕ
Вариант 1
1. Решить неравенство  ≥ 0.
≥ 0.
2. Тело движется по закону х( t )= t 3 -2 t 2 +5 (х – в метрах, t – в секундах). Найдите скорость и ускорение тела через 2с после начала движения.
3. Исследовать функцию f(х)= х2 + 7х – 4 на монотонность и экстремумы.
4. Найти наибольшее и наименьшее значения функции f(х)= х3- 6 х2 на
отрезке [-2;5].
5. Составьте уравнение касательной к графику функции f(х)= х2 + 2х в точке х0=1.
Вариант 2
1. Решить неравенство 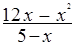 ≤ 0.
≤ 0.
2. Тело движется по закону х( t )= 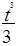 + 6 t - 1 (х – в метрах, t – в секундах). Найдите скорость и ускорение тела через 5с после начала движения.
+ 6 t - 1 (х – в метрах, t – в секундах). Найдите скорость и ускорение тела через 5с после начала движения.
3. Исследовать функцию f(х)=10 – 4х - х2 на монотонность и экстремумы.
4. Найти наибольшее и наименьшее значения функции f(х)= 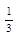 х3- х на
х3- х на
отрезке [0;4].
5. Составьте уравнение касательной к графику функции f(х)= х2-3х+2 в точке х0=
ОТВЕТЫ к контрольной работе «ПРОИЗВОДНАЯ И ЕЁ ПРИЛОЖЕНИЕ»
| № задания | Вариант 1 | Вариант 2 |
| 1 | [0; 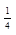 ] ] 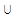 (7; ∞) (7; ∞)
| (-∞;0] 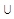 [5;12) [5;12)
|
| 2 | 4м/с; 8м/с2 | 31м/с; 10м/с2 |
| 3 | f ↓ на х 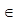 (-∞;-3,5),
f ↑ на х (-∞;-3,5),
f ↑ на х 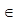 (-3,5; ∞)
х=-3,5 точка min (-3,5; ∞)
х=-3,5 точка min
| f ↑ на х 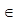 (-∞;-2),
f ↓ на х (-∞;-2),
f ↓ на х 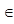 (-2; ∞)
х=-2 точка max (-2; ∞)
х=-2 точка max
|
| 4 | уmax=0; уmin=-32 [-2;5] [-2;5] | уmax= 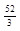 ; уmin= - ; уmin= - 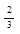 ;
[0;4] [0;4] ;
[0;4] [0;4]
|
| 5 | у=4х-1 | у = 1-5 х |
Контрольная работа №6
Интеграл и ее приложение
Вариант 1 Часть 1
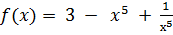 ;
2)
;
2) 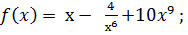 3)
3) 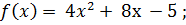 4)
4) 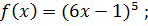 5)
5) 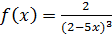 .
.
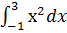 2)
2)  3)
3) 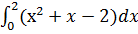 .
4)
.
4) 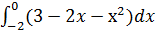 5)
5) 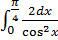
|
Вариант 2 Часть 1 | |
2. Найти общий вид первообразных:
1)  ;
2) ;
2) 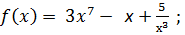 3)
3) 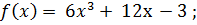 4)
4) 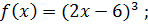 5)
5) 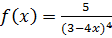 . .
| 2. Вычислить интегралы:
1) 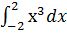 ;
2) ;
2) 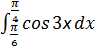 ;
3) ;
3) 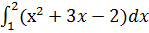 ;
4) ;
4) 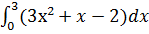 ;
5) ;
5) 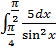 . .
|
Часть 2. Вариант 1
1. Найти общий вид первообразных для функции
a) f(x)= 4sin x + cos3x ;
б) f ( x )= x 2 + 2 x .
2. Найти первообразную функции f ( x )=5х + x 2 , график которой проходит через точку (1;3).
3. Вычислить интеграл 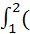 х2 +х)dx .
х2 +х)dx .
4. Вычислить площадь фигуры, ограниченной линиями
у = 3- х и у = - х2+2х+3.
Часть 2. Вариант2
1. Найти общий вид первообразных для функции
а ) f(x)= 3cos x + sin4x;
б) f ( x )= х5 + x 2 .
2. Найти первообразную функции f ( x )=3 x 2 -5, график которой проходит через точку (2;10).
3. Вычислить интеграл 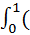 х2 +2х)dx
х2 +2х)dx
4. Вычислить площадь фигуры, ограниченной линиями
у = 3+2х и у = х2-2х+3.
| ОТВЕТЫ | ||
| Вариант1 | Вариант 2 | |
| 1. | 1) 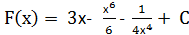 ;
2) ;
2) 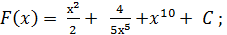 3)
3) 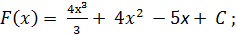 4)
4) 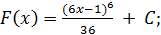 5)
5) 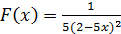 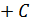 . .
| 1) 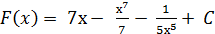 ;
2) ;
2) 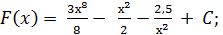 3)
3) 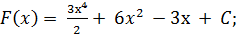 4)
4) 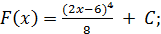 5)
5) 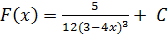 . .
|
| 2. | 1) 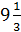 ;
2) 1 ;
3) ;
2) 1 ;
3)  ;
4) ;
4) 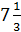 ;
5) 2. ;
5) 2.
| 1) 0 ;
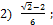
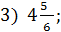 4) 25,5 ;
5) 5.
4) 25,5 ;
5) 5.
|
Ответы
| № варианта | Задание 1 а) | Задание 1 б) | Задание 2 | Задание 3 | Задание 4 |
| 1 | - 4 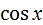 + +  +С +С
| 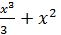 + С + С
| 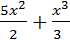 + + 
| 3 
| 4,5 |
| 2 | 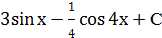
| 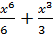 + С + С
| х3- 5х +12 | 1 
| 10 
|
Контрольная работа №7
Показательные, логарифмические уравнения и неравенства.
Часть 1.
Вариант 1
1. Вычислите 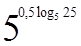 .
.
2. Найдите область определения функции у = lg 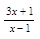 .
.
3. Решите уравнения:
а) log2 (4х - 1)= 3;
б) log7 2 = 1- log7 (5 - х).
4. Решите неравенства:
а) log5 (1 - 4х) ≤ 2;
б) log 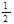 (2х + 3) > -3.
(2х + 3) > -3.
Вариант 2
1. Вычислите 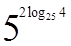 .
.
2. Найдите область определения функции у = lg 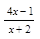 .
.
3. Решите уравнения:
а) log4 (2х - 1)= 2;
б) log2 (2х + 3) = log 2 4 + 1.
4. Решите неравенства: 
а) log3 (2 - 3х) ≥ 2;
б) 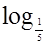 (х + 1) > -2.
(х + 1) > -2.
Вариант 3
1. Вычислите 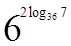 .
.
2. Найдите область определения функции у = lg 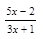 .
.
3. Решите уравнения:
а) log5 (6х - 1)= 2;
б) log3 (4х + 5) = log3 9 + 1.
4. Решите неравенства: 
а) log4 (2 - 5х) ≥ 3;
б) 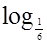 (х - 1) > -1.
(х - 1) > -1.
Вариант 4
1. Вычислите 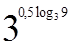 .
.
2. Найдите область определения функции у = lg 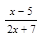 .
.
3. Решите уравнения:
а) log3 (7х - 2)= 2;
б) log7 (2х + 5) = log749 + 2.
4. Решите неравенства: 
а) log4 (5 - х) ≥ 0;
б) 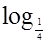 (3х - 1) > - 1 .
(3х - 1) > - 1 .
Вариант 5
1. Вычислите 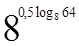 .
.
2. Найдите область определения функции у = lg 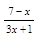 .
.
3. Решите уравнения:
а) 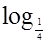 (х - 2)= - 2;
(х - 2)= - 2;
б) log5 (2х - 3) = log525 - 2.
4. Решите неравенства: 
а) log9 (3 - х) ≤ 0;
б) 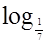 (3х - 1) < - 1 .
(3х - 1) < - 1 .
Вариант 6
1. Вычислите 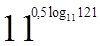 .
.
2. Найдите область определения функции у = lg 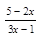 .
.
3. Решите уравнения:
а) 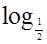 (х - 2)= - 3;
(х - 2)= - 3;
б) log8 (2х - 3) = log81 - 1.
4. Решите неравенства: 
а) log4 (8 - х) ≤ 2;
б) 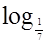 (2х - 1) < 0 .
(2х - 1) < 0 .
Вариант 7
1. Вычислите 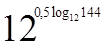 .
.
2. Найдите область определения функции у = lg 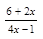 .
.
3. Решите уравнения:
а) 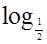 (2х - 1)= - 4;
(2х - 1)= - 4;
б) log3 (х - 3) = log327 - 1.
4. Решите неравенства: 
а) log5 (5 - х) ≤ 2;
б) 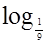 (х + 3) < - 1 .
(х + 3) < - 1 .
Вариант 8
1. Вычислите 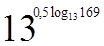 .
.
2. Найдите область определения функции у = lg 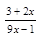 .
.
3. Решите уравнения:
а) 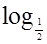 (х - 2)= 0;
(х - 2)= 0;
б) log3 (х + 9) = log381 - 3.
4. Решите неравенства: 
а) log5 (х - 6) ≤ 2;
б) 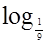 (х + 5) > - 2 .
(х + 5) > - 2 .
Вариант 9
1. Вычислите 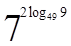 .
.
2. Найдите область определения функции у = lg 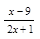 .
.
3. Решите уравнения:
а) log8 (5х - 2)= 1;
б) log6 (х + 5) = log6 36 + 1.
4. Решите неравенства: 
а) log5 (3 - х) ≥ 0;
Часть 2.
Вариант 1/5
1. Дайте определение логарифма данного числа по данному основанию.
2. 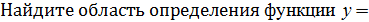
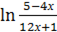
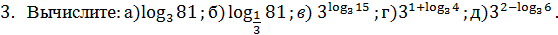
4. Найдите х, если 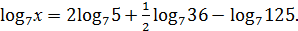
5. Вычислите 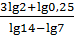 .
.
Вариант 2/6
1. Сформулируйте основные свойства логарифмов.
2. 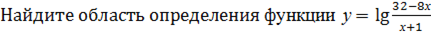 .
.
3. Вычислите: 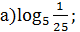
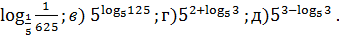
4. Найдите х, если 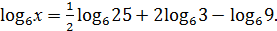
5. Вычислите 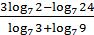 .
.
Вариант 3/7
1. Какая функция называется логарифмической? Сформулируйте основные свойства логарифмической функции при а>0.
2. 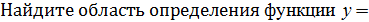
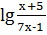 .
.
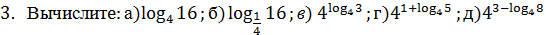
4. Найдите х, если 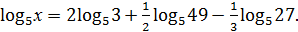
5. Вычислите 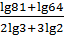 .
.
Вариант 4/8/9
1. Запишите основное логарифмическое тождество.
2. 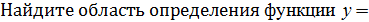
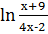 .
.
3. Вычислите: 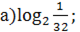
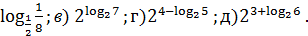
4. Найдите х, если 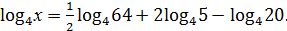
5. Вычислите 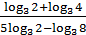 .
.
Часть 3.
Вариант 1-5
1. 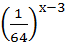 = 23-2х;
2. 7х+2 - 14∙7х = 5;
3. 49х - 8∙7х + 7 = 0;
4. = 23-2х;
2. 7х+2 - 14∙7х = 5;
3. 49х - 8∙7х + 7 = 0;
4. 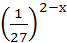 > 92х-1;
5. 10∙5х-1 + 5х+1 < 7. > 92х-1;
5. 10∙5х-1 + 5х+1 < 7.
|
Часть 3.
Вариант 6-9
1. 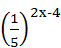 = 1253-4х;
2. 2х+4 - 2х = 120;
3. 36х - 4∙6х - 12 = 0;
4. = 1253-4х;
2. 2х+4 - 2х = 120;
3. 36х - 4∙6х - 12 = 0;
4. 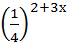 < 8х-1;
5. 8∙2х-1 - 2х > 48. < 8х-1;
5. 8∙2х-1 - 2х > 48.
|
Ответы «Логарифмы»
| № задания | Вариант 1 | Вариант 2 | Вариант 3 | Вариант 4 | Вариант 5 | Вариант 6 | Вариант 7 | Вариант 8 | Вариант 9 |
| 1 | 5 | 4 | 7 | 3 | 8 | 11 | 12 | 13 | 9 |
| 2 | (-∞;- 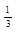 ) )
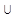 (1; ∞) (1; ∞)
| (-∞;-2) 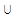 ( ( 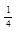 ;∞) ;∞)
| (-∞;- 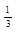 ) )
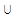 (0,4;∞) (0,4;∞)
| (-∞;-3,5)
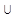 (5;∞) (5;∞)
| (- 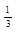 ;7) ;7)
| ( 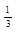 ;2,5) ;2,5)
| (-∞;-3)
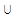 ( ( 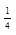 ;∞) ;∞)
| (-∞;-1,5)
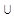 ( ( 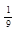 ;∞) ;∞)
| (-∞;-0,5)
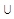 (9;∞) (9;∞)
|
| 3 а) | 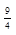
| 8,5 | 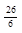
| 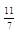
| 18 | 10 | 8,5 | 3 | 2 |
| 3 б) | 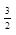
| 2,5 | 5,5 | 1198 | 2 | 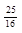
| 12 | -6 | 211 |
| 4 а) | [-6; 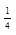 ) )
| (-∞;- 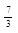 ] ]
| (-∞;-12,4] | (-∞;4] | [2;3) | [-8;8) | [-20;5) | (6;31] | (-∞;2] |
| 4 б) | (-1,5;2,5) | (-1;24) | (1; 7) | ( 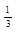 ; ; 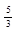 ) )
| ( 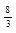 ;∞) ;∞)
| (1; ∞) | (6; ∞) | (-5;76) | (1;17) |
ОТВЕТЫ
«РЕШЕНИЕ ПОКАЗАТЕЛЬНЫХ УРАВНЕНИЙ И НЕРАВЕНСТВ»
| № варианта | Задание 1 | Задание 2 | Задание 3 | Задание 4 | Задание 5 |
| 1 | 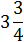
| -1 | 1; 0 | х < -4 | х < 0 |
| 2 | 
| 3 | 1 | х > 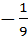
| х >4 |
ОТВЕТЫ к зачёту «Свойства логарифмов и логарифмической функции»
| № варианта Задание № | Вариант 1 | Вариант 2 | Вариант 3 | Вариант 4 |
| 1. | Логарифмом числа в по осно-ванию а называ-ется показатель степени, в кото-рую нужно воз-вести основание а, чтобы полу-чить число в.
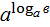 =в. =в.
| 1) 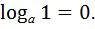 2)
2) 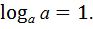 3)
3) 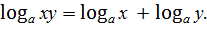 4)
4) 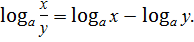 5)
5) 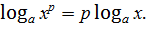
| Функцию, задан-
ную формулой
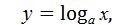 называют лога-рифмической функцией с ос-нованием а.
называют лога-рифмической функцией с ос-нованием а.
| 1) D( 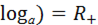 2) Е(
2) Е( 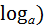 = = 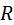 .
3) Логарифми-
ческая функция на всей области определения возрастает
(при а>0)
или убывает
(при 0<а<1). .
3) Логарифми-
ческая функция на всей области определения возрастает
(при а>0)
или убывает
(при 0<а<1).
|
| 2. | ( 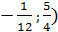
| (-1;4) | (-∞;-5) 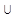 ( ( 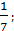 ∞) ∞)
| (-∞;-1) 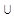 ( ( 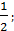 ∞) ∞)
|
| 3. | а) 4; б) -4; в) 15; г) 12; д) 1,5. | а) -2;
б) 4;
в) 125;
г) 75;
д) 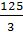 . .
| а) 2; б) -2; в) 3; г) 20; д) 8. | а) -5;
б) 3;
в) 7;
г) 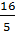 ;
д) 48. ;
д) 48.
|
| 4. | 
| 5 | 21 | 10 |
| 5. | 1 | 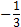
| 2 | 
|
Контрольная работа №8
Дата: 2018-12-21, просмотров: 446.