РАЗДЕЛ 1. МЕТОДЫ ОПИСАТЕЛЬНОЙ СТАТИСТИКИ
Тема1. Выборочный метод
Понятие выборочной и генеральной совокупности
Большинство педагогических исследований призвано ответить на вопрос, верно ли сделанное исследователем предположение, подтверждается ли выдвинутая им гипотеза. Наиболее привлекательным с точки зрения эффективности и целесообразности методом психолого-педагогического исследования является опыт. Однако, сами результаты опыта, как правило, не позволяют нам сделать чётких и научно обоснованных выводов о справедливости (или ложности) выдвинутой гипотезы. Проанализировать результаты опыта и сделать полезные выводы помогают математические методы исследования.
Очевидно, что в большинстве случаев невозможно поставить опыт над всем множеством объектов, в отношении которых формулируется исследовательская гипотеза. Такое множество носит название генеральной совокупности. Например, при желании понять, каким образом меняется успеваемость учащихся при использовании той или иной модели обучения, исследователь должен был бы провести эксперимент с каждым учеником. Но такой метод затруднителен в силу его трудоёмкости, дороговизны и длительности. Поэтому педагогические и психологические опыты, как правило, производятся не над всей генеральной совокупностью исследуемых объектов, а лишь над их частью, называемой выборкой. При этом отдельный индивид из выборки, с которым работает экспериментатор, называется испытуемым (респондентом). Таким образом, эксперимент, а затем и анализ полученных результатов осуществляется над выборкой.
Теоретически считается, что объем генеральной совокупности, обозначаемый буквой N, не ограничен. Практически же объем генеральной совокупности всегда ограничен и может быть различным в зависимости от предмета наблюдения и той задачи, которую предстоит решать экспериментатору.
Объем выборки, обычно обозначаемой буквой n , может быть любым, но не меньшим чем два респондента. В статистике различают малую 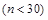 , среднюю
, среднюю 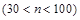 и большую выборки
и большую выборки 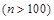 .
.
Требования к выборке
К выборке применяется ряд обязательных требований, определенных, прежде всего, целями и задачами исследования. Планирование эксперимента должно включать в себя учет как объема выборки, так и ряда ее особенностей. Так, в психологических исследованиях важно требование однородности выборки. Оно означает, что психолог, изучая, например, подростков, не может, включать в эту же выборку взрослых людей. Напротив, исследование, выполненное методом возрастных срезов, принципиально предполагает наличие разновозрастных испытуемых. Однако и в этом случае должна соблюдаться однородность выборки, но уже по другим критериям, в первую очередь таким, как возраст, пол. Основаниями для формирования однородной выборки могут служить разные характеристики, такие, как уровень интеллекта, национальность, отсутствие определенных заболеваний и т.д., в зависимости от целей исследования.
В общей статистике имеется понятие повторной и бесповторной выборки, или, иначе говоря, выборки с возвратом и без возврата. В качестве примера приводится, как правило, выбор шара, доставаемого из какой-либо емкости. В случае выборки с возвратом каждый выбранный шар опять возвращается в емкость и, следовательно, может быть выбран снова. При бесповторном выборе однажды выбранный шар откладывается в сторону и больше не может участвовать в выборке. В психологических исследованиях можно найти аналоги подобного рода способам организации выборочного исследования, поскольку психологу нередко приходится несколько раз тестировать одних и тех же испытуемых при помощи одной и той же методики. Однако, строго говоря, повторной в этом случае является процедура тестирования. Выборка испытуемых при полной тождественности состава в случае повторных исследований всегда будет иметь некоторые отличия, обусловленные функциональной и возрастной изменчивостью, присущей всем людям. Подобная выборка по характеру проведения процедуры является повторной, хотя смысл термина здесь, очевидно, иной, чем в случае с шарами.
Важно подчеркнуть, что все требования, предъявляемые к любой выборке, сводятся к тому, что на ее основе психологом должна быть получена наиболее полная, неискаженная информация об особенностях генеральной совокупности, из которой взята эта выборка. Иными словами, выборка должна как можно более полно отражать характеристики изучаемой генеральной совокупности.
Репрезентативность выборки
Состав экспериментальной выборки должен представлять (моделировать) генеральную совокупность, поскольку выводы, полученные в эксперименте, предполагается в дальнейшем перенести на всю генеральную совокупность. Поэтому выборка должна обладать особым качеством – репрезентативностью, позволяющей распространить полученные на ней выводы на всю генеральную совокупность.
Репрезентативность выборки очень важна, тем не менее по объективным причинам соблюдать её крайне сложно. Так, хорошо известен факт, что от 70% до 90% всех психологических исследований поведения человека проводились в США в 60-х годах XX века с испытуемыми – студентами колледжей, причем большинство из них были студентами психологами. В лабораторных исследованиях, выполняемых на животных, наиболее распространенным объектом изучения являются крысы. Поэтому неслучайно психологию называли раньше «наукой о студентах-второкурсниках и белых крысах». Студенты колледжей составляют всего 3% от общей численности населения США. Очевидно, что выборка студентов нерепрезентативна в качестве модели, претендующей на представительство всего населения страны.
Репрезентативная выборка, или, как еще говорят, представительная выборка, – это такая выборка, в которой все основные признаки генеральной совокупности представлены приблизительно в той же пропорции и с той же частотой, с которой данный признак выступает в данной генеральной совокупности. Иными словами, репрезентативная выборка представляет собой меньшую по размеру, но точную модель той генеральной совокупности, которую она должна отражать. В той степени, в какой выборка является репрезентативной, выводы, основанные на изучении этой выборки, можно с большой долей уверенности считать применимыми ко всей генеральной совокупности. Это распространение результатов называется генерализуемостью.
В идеале репрезентативная выборка должна быть такой, чтобы каждая из основных изучаемых психологом характеристик, черт, особенностей личности и т.п. была бы представлена в ней пропорционально этим же особенностям в генеральной совокупности. Согласно этим требованиям процедура формирования выборки должна иметь внутреннюю логику, способную убедить исследователя, что при сравнении с генеральной совокупностью она действительно окажется репрезентативной, представительной.
Нарушение принципов случайного выбора порой приводило к серьезным ошибкам. Стал знаменитым своей неудачей опрос, проведенный американским журналом «Литературное обозрение» относительно исхода президентских выборов в США в 1936 году.
Кандидатами на этих выборах были Ф.Д. Рузвельт и А.М. Ландон. В качестве генеральной совокупности редакция журнала использовала телефонные книги. Отобрав случайно 4 миллиона адресов, она разослала по всей стране открытки с вопросом об отношении к кандидатам в президенты. Затратив большую сумму на рассылку и обработку открыток, журнал объявил, что на предстоящих выборах президентом США с большим перевесом будет избран Ландон. Результат выборов оказался противоположным этому прогнозу.
Здесь были совершены сразу две ошибки – во-первых, телефонные книги сами по себе дают не репрезентативную выборку из населения страны, хотя бы потому, что абоненты – в основном зажиточные главы семейств. Во-вторых, прислали ответы не все, а люди, не только достаточно уверенные в своем мнении, но и привыкшие отвечать на письма, т.е. в значительной части представители делового мира, которые и поддерживали Ландона. Если бы редакция критически подошла к своей работе, она поняла бы, что методика опроса страдает изъянами.
Явление, подобное только что описанному, когда выборка представляет не всю генеральную совокупность, а лишь какой-то ее слой, какую-то ее часть, называется смещением выборки. Смещение – один из основных источников ошибок при использовании выборочного метода.
Однако для тех же самых президентских выборов социологи Дж. Гэллап и Э. Роупер правильно предсказали победу Рузвельта, основываясь только на 4 тысячах анкет. Причиной этого успеха, прославившего его авторов, было не только правильное составление выборки. Они учли, что общество распадается на социальные группы, которые более однородны, в том числе по своим политическим взглядам. Поэтому выборка из слоя может быть относительно малочисленной с тем же результатом точности. Имея результаты обследования по слоям, можно характеризовать общество в целом. Сейчас такая методика является общепринятой.
В своей конкретной деятельности психолог действует следующим образом: устанавливает подгруппу (выборку) внутри генеральной совокупности, подробно изучает эту выборку (проводит с ней экспериментальную работу), а затем, если позволяют результаты статистического анализа, распространяет полученные выводы на всю генеральную совокупность. Это и есть основные этапы работы психолога с выборкой.
Начинающий психолог должен иметь в виду часто повторяющуюся ошибку: каждый раз, когда он осуществляет сбор любых данных любым методом и из любого источника, у него всегда появляется соблазн распространить свои выводы на всю генеральную совокупность. Для того чтобы избежать подобной ошибки, надо не просто обладать здравым смыслом, но, прежде всего, хорошо владеть основными понятиями математической статистики.
Формирование выборки
Возникает закономерный вопрос: как сформировать репрезентативную выборку? С точки зрения статистики, репрезентативность выборки означает, что представленное в выборке распределение изучаемых признаков соответствует (с определенной долей погрешности) их распределению в генеральной совокупности.
Опишем два метода, обеспечивающие репрезентативность выборки.
Первый метод – формирование простой случайной выборки. В этом случае выборка состоит из элементов, отобранных из генеральной совокупности таким образом, чтобы каждый элемент этой совокупности имел равные возможности (равную вероятность) попасть в выборку. Полученная таким образом выборка называется простой случайной выборкой.
Получить простую случайную выборку можно путем обычной жеребьевки (по аналогии с лотереей) или с помощью специальных таблиц случайных чисел. В последнем случае элементы генеральной совокупности перенумеровываются и из таблицы случайных чисел, открытой на произвольной странице, выписываются номера элементов, которые должны быть взяты в выборку. Данная процедура трудно осуществима, поскольку для ее реализации необходимо учитывать каждого представителя генеральной совокупности.
Второй метод основывается на понятии стратифицированной случайной выборки. Для этого необходимо разбить элементы генеральной совокупности на страты (группы) в соответствии с некоторыми характеристиками. Например, при обследовании спроса на некоторый товар генеральную совокупность желательно разбить на группы, различающиеся по величине дохода, социальной принадлежности или даже по месту жительства (город, деревня). Если произведена подобная разбивка совокупности и случайная выборка производится отдельно из каждой группы (страты), то полученная в итоге выборка носит название стратифицированная случайная выборка.
ВОПРОСЫ И УПРАЖНЕНИЯ
1. Дайте определение следующим понятиям: выборка и генеральная совокупность; выборочное и сплошное исследования; зависимые и независимые выборки; выборки повторные и бесповторные.
2. Дайте характеристики следующим выборкам: однородная, простая, случайная, стратифицированная, репрезентативная.
3. Перечислите и охарактеризуйте методы формирования выборки и методы определения ее объема.
4. Экспериментатор ставит целью своего исследования доказать различия в результативности обучения чтению в двух группах первоклассников, обучающихся по разным методикам. Определите для исследования требования к выборкам учащихся.
Группировка данных
Группировка – это объединение вариант в интервалы, границы которых устанавливаются произвольно и непременно указываются. Получаемая в итоге величина называется частотой появления признака.
Группировка данных – это суммирование частоты появления признака или некоторых значений признаков в изучаемом массиве объектов по определенным позициям. Математический смысл обработки исходных данных при использовании метода группировки заключается в суммировании данных по частоте появлений некоторых значений.
Наиболее легким из известных методов обработки является метод простой группировки данных. Например, результаты тестирования студентов 1-го курса по философии распределились следующим образом:
1 – ответили на «отлично» – 10 чел.;
2 – ответили на «хорошо» – 34 чел.;
3 – ответили на «удовлетворительно» – 94 чел.;
4 – получили «неудовлетворительно» – 18 чел.;
5 – не участвовали в тестировании – 12 чел.
Табулирование данных
Наиболее распространенной формой группировки экспериментальных данных являются статистические таблицы. Таблицы бывают сложные и простые.
К простым относятся таблицы, применяемые при альтернативной группировке, когда одна группа испытуемых противопоставляется другой; например, здоровые – больным, высокие люди – низким и т.п.
Пример простой таблицы приведен ниже (таб. 2.1). В ней представляются результаты обследования мануальной асимметрии у 110 учащихся 3-6-х классов.
Таблица 2.1
| Классы | Праворукие | Леворукие | Сумма |
| 3 и 4 | 43 | 6 | 49 |
| 5 и 6 | 44 | 17 | 61 |
| Сумма | 87 | 23 | 110 |
Усложнение таблицы рекомендуется использовать, когда измерение изучаемых признаков производится в номинативной или порядковой шкале.
Усложнение таблицы происходит за счет возрастания объема и степени дифференцированности представленной в них информации. К сложным таблицам относятся так называемые многопольные таблицы, которые могут использоваться при выяснении причинно-следственных отношений между варьирующими признаками.
Примером сложной таблицы служит таблица 2.2, в которой представлены классические данные Ф. Гальтона, иллюстрирующие наличие положительной зависимости между ростом родителей и их детей. Таблица организована таким образом, что позволяет оценить частоту встречаемости в популяции однозначно фиксируемых соотношений роста родителей и роста ребенка.
Таблица 2.2
Рост родителей
Рост детей в дюймах
Всего
Правильно составленные таблицы – это большое подспорье в экспериментальной работе, позволяющее одновременно осуществлять разные варианты группировки полученных данных.
Ранговый порядок
Ранжирование – это расположение данных в порядке возрастания или убывания.
Ранжирование может быть простым и принудительным.
При простом ранжировании количество рангов меньше количества ранжируемых признаков.
Например, можно разделить группу людей, претендующих на должность менеджера, по признаку соответствия предъявляемым требованиям:
- ранг 1 получат претенденты, соответствующие предъявляемым требованиям;
- ранг 2 – претенденты частично соответствующие требованиям;
- ранг 3 – претенденты, несоответствующие требованиям.
В этих случаях не всегда можно все признаки уместить в несколько рангов. Признаки, имеющие один ранг, могут сильно отличаться.
Принудительное ранжирование используется в случае, когда количество рангов равно количеству признаков.
При принудительном ранжировании разные ранги могут искусственно преувеличивать расстояние между рангами. В разных группах один испытуемый может иметь ранг, отличный от того, какой он имел бы в другой группе.
РАСПРЕДЕЛЕНИЕ ЧАСТОТ
При описании общей картины результатов теста список студентов из таблицы можно сократить, классифицируя баллы по распределению частот, иногда называемому распределением.
Числа, показывающие, сколько раз варианты встречаются в данной совокупности, называются частотами, или весами вариант. Они обозначаются fi и имеют индекс « i », соответствующий номеру переменной.
Частость (относительная частота) – доля каждой частоты fi в общем объеме выборки n:
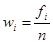 . (2.2)
. (2.2)
В таблице 2.4 приведен пример нахождения частоты и частости результатов тестирования из таблицы 2.3.
В случае большого диапазона разброса данных имеет смысл обобщение данных в виде группирования по интервалам. Правила выбора количества интервалов не существует, но предпочтительно группировать по 12-15 интервалам (классам).
Ширина интервалов (класса) должна быть одинаковой и равной
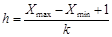 , (2.3)
, (2.3)
где h – ширина интервалов; k – количество классов; Xmax – максимальное значение из данных; Xmin – минимальное значение из данных.
Количество классов выбирается таким образом, чтобы ширина была целым числом.
Задача 2.1. Данные из таблицы 2.4 необходимо разбить на интервалы, найти середины интервалов, а также частоту и частость в интервалах.
Таблица 2.4
| Баллы, Х i | Частота, fi | Частость, wi |
| 71 | 1 | 0,1 |
| 73 | 1 | 0,1 |
| 75 | 3 | 0,3 |
| 84 | 1 | 0,1 |
| 87 | 1 | 0,1 |
| 88 | 2 | 0,2 |
| 90 | 1 | 0,1 |
| Сумма | 10 | 1,0 |
Максимальный балл равен 90 баллам, минимальный – 71. Ширина определяется по формуле (2.3):
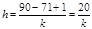 .
.
Для того чтобы ширина была целым числом, количество интервалов должно быть или 4, или 5, или 10.
Найдем ширину интервалов при количестве интервалов, равном пяти:
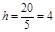 .
.
Определение середины интервала состоит в усреднении зафиксированных границ интервала. Например, для первого интервала середина будет (74+71)/2=72,5. Занесем все вычисления в таблицу 2.5.
Таблица 2.5
| Интервал | Середина интервала | Частота | Относительная частота |
| 71-74 | 72,5 | 2 | 0,2 |
| 75-78 | 76,5 | 3 | 0,3 |
| 79-82 | 80,5 | ||
| 83-86 | 84,5 | 1 | 0,1 |
| 87-90 | 88,5 | 4 | 0,4 |
| Сумма | 10 | 1,0 |
СТАТИСТИЧЕСКИЕ РЯДЫ
Особую форму группировки данных представляют так называемые статистические ряды, или числовые значения признака, расположенного в определенном порядке.
В зависимости от того, какие признаки изучаются, статистические ряды делят на атрибутивные, вариационные, ряды динамики, регрессии, ряды ранжированных значений признаков и ряды накопленных частот. Наиболее часто в психологии используются вариационные ряды, ряды регрессии и ряды ранжированных значений признаков.
Вариационным рядом распределения называют двойной ряд чисел, показывающий, каким образом числовые значения признака связаны с их повторяемостью в данной выборке. Например, результаты вступительного тестирования оказались следующими:
71, 75, 84, 75, 87, 84, 75, 88, 90, 88.
Как видим, некоторые цифры попадаются в данном ряду по несколько раз. Следовательно, учитывая число повторений, данные ряда можно представить в более удобной, компактной форме:
| Варианты | xi | 73 | 71 | 75 | 87 | 84 | 88 | 90 | (2.4) |
| Частоты вариант | fi | 1 | 1 | 3 | 1 | 1 | 2 | 1 |
Это и есть вариационный ряд. Числа, показывающие, сколько раз отдельные варианты встречаются в данной совокупности, называются частотами, или весами, вариант. Они обозначаются строчной буквой латинского алфавита и имеют индекс «i», соответствующий номеру переменной в вариационном ряду.
Общая сумма частот вариационного ряда равна объему выборки, т.е.
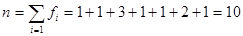 .
.
Частоты можно выражать и в процентах. При этом общая сумма частот или объем выборки принимается за 100%. Процент каждой отдельной частоты или веса подсчитывается по формуле:
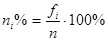 . (2.5)
. (2.5)
Процентное представление частот полезно в тех случаях, когда приходится сравнивать вариационные ряды, сильно различающиеся по объемам. Например, при тестировании школьной готовности детей города, поселка городского типа и села были обследованы выборки детей численностью 1000, 300 и 100 человек соответственно. Различие в объемах выборок очевидно. Поэтому сравнение результатов тестирования лучше проводить, используя проценты частот.
Приведенный выше ряд (2.4) можно представить по-другому. Если элементы ряда расположить в возрастающем порядке, то получится так называемый ранжированный вариационный ряд:
| Варианты | xi | 71 | 73 | 75 | 84 | 87 | 88 | 90 | (2.6) |
| Частоты вариант | fi | 1 | 1 | 3 | 1 | 1 | 2 | 1 |
Подобная форма представления (2.6) более предпочтительна, чем (2.4), поскольку лучше иллюстрирует закономерность варьирования признака.
Частоты, характеризующие ранжированный вариационный ряд, можно складывать или накапливать. Накопленные частоты получаются последовательным суммированием значений частот от первой частоты до последней.
В качестве примера вновь обратимся к ряду (2.6). Преобразуем его в ряд (2.7), в котором введем дополнительную строчку и назовем ее «кумуляты частот».
| Варианты | xi | 71 | 73 | 75 | 84 | 87 | 88 | 90 | |
| Частоты вариант | fi | 1 | 1 | 3 | 1 | 1 | 2 | 1 | (2.7) |
| Кумуляты частот | 1 | 2 | 5 | 6 | 7 | 9 | 10 |
Статистические функции в MS Excel (функции МАКС, МИН, РАНГ, ЧАСТОТА)
В Excel есть огромное количество инструментов, которые помогают проводить статистическую обработку данных. Последние версии этой программы в плане возможностей практически ничем не уступают специализированным приложениям в области статистики.
Главными инструментами для выполнения расчетов и анализа являются функции. Как и любые другие функции в Excel, статистические функции оперируют аргументами, которые могут иметь вид постоянных чисел, ссылок на ячейки или массивы.
Выражения можно вводить вручную в определенную ячейку или в строку формул, если хорошо знать синтаксис конкретного из них. Но намного удобнее воспользоваться специальным окном аргументов, которое содержит подсказки и уже готовые поля для ввода данных.
Перейти в окно аргумента статистических выражений можно через «Мастер функций» или с помощью кнопок «Библиотеки функций» на ленте. Запустить Мастер функций можно тремя способами:
1. Кликнуть по пиктограмме «Вставить функцию» слева от строки формул (рис. 2.7).
|
| Рис. 2.7. Пиктограмма «Вставить функцию» |
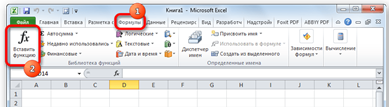
2. Находясь во вкладке «Формулы», кликнуть на ленте по кнопке «Вставить функцию» в блоке инструментов «Библиотека функций» (рис. 2.8).
|
| Рис. 2.8. Вкладка «Формулы» |
|
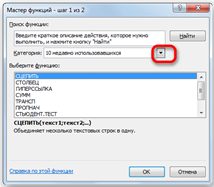
| Рис. 2.9. Окно «Мастер функций» |
|
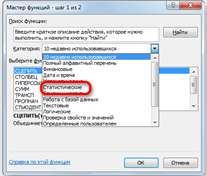
| Рис. 2.10. Категория «Статистические» |
|
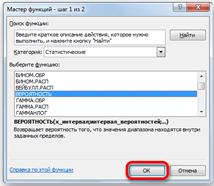
| Рис. 2.11. Перечень статистических функций |
3. Набрать на клавиатуре сочетание клавиш Shift+F3.
При выполнении любого из вышеперечисленных вариантов откроется окно «Мастера функций» (рис.2.9).
Затем нужно кликнуть по полю «Категория» и выбрать значение «Статистические» (рис. 2.10).
После этого откроется список статистических выражений. Всего их насчитывается более сотни. Чтобы перейти в окно аргументов любого из них, нужно просто выделить его и нажать на кнопку «OK» (рис. 2.11).
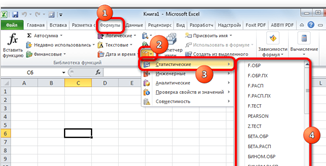
Для того, чтобы перейти к нужным нам элементам через ленту, перемещаемся во вкладку «Формулы». В группе инструментов на ленте «Библиотека функций» кликаем по кнопке «Другие функции». В открывшемся списке выбираем категорию «Статистические». Откроется перечень доступных элементов нужной нам направленности. Для перехода в окно аргументов достаточно кликнуть по одному из них (рис.2.12).
|
| Рис. 2.12. «Библиотека функций» |
Функция МАКС
Предназначена для определения максимального числа из выборки. Она имеет следующий синтаксис:
=МАКС(число1;число2;…)
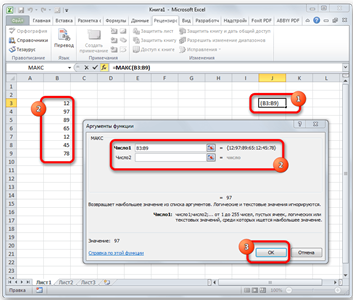
В поля аргументов нужно ввести диапазоны ячеек, в которых находится числовой ряд. Наибольшее число из него эта формула выводит в ту ячейку, в которой находится сама (рис. 2.13).
|
| Рис. 2.13. Функция МАКС |
Функция МИН
Её задачи прямо противоположны предыдущей формуле – она ищет из множества чисел наименьшее и выводит его в заданную ячейку. Имеет такой синтаксис:
=МИН(число1;число2;…)
Функция РАНГ (РАНГ.РВ)
В версиях Excel, начиная с 2010 года, появилась функция РАНГ.РВ. Это абсолютный аналог функции РАНГ. Синтаксис такой же. Буквы «РВ» в названии указывают на то, что при обнаружении формулой одинаковых значений функция вернет высший номер ранжирования (то есть первого обнаруженного элемента в перечне равных) (рис. 2.14).
=РАНГ.РВ(число;ссылка;[порядок])
· Число (обязательный) – число, для которого определяется ранг.
· Ссылка (обязательный) – массив чисел или ссылка на список чисел. Нечисловые значения в ссылке игнорируются.
· Порядок (необязательный) – число, определяющее способ упорядочения.
Замечания:
1. Если значение аргумента «порядок» равно 0 (нулю) или опущено, ранг числа определяется в Excel так, как если бы ссылка была списком, отсортированным по убыванию.
2. Если значение аргумента «порядок» — любое число, кроме нуля, то ранг числа определяется в Excel так, как если бы ссылка была списком, отсортированным по возрастанию.
3. Функция РАНГ.РВ присваивает повторяющимся числам одинаковые значения ранга. Однако наличие повторяющихся чисел влияет на ранги последующих чисел. Например, если в списке целых чисел, отсортированных по возрастанию, дважды встречается число 10, имеющее ранг 5, число 11 будет иметь ранг 7 (ни одно из чисел не будет иметь ранга 6).
Функция РАНГ.СР
Аналогична функции РАНГ.РВ, отличие состоит в том, при обнаружении идентичных значений возвращает средний показатель.
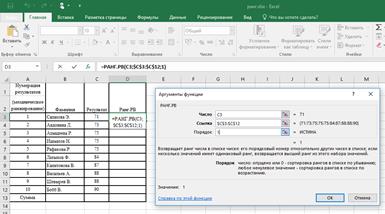
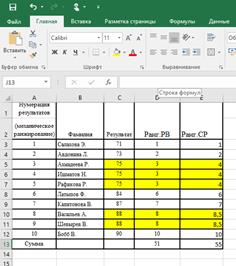
Рассчитаем ранг для данных задачи 2.1. и сравним ранги, полученные с помощью функций РАНГ.РВ и РАНГ.СР (рис. 2.15).
|
| Рис. 2.14. Функция РАНГ.РВ |
|
| Рис. 2.15. Сравнение функций РАНГ.РВ и РАНГ.СР |
Функция ЧАСТОТА
Подсчитывает количество значений, попадающих в заданные интервалы («карманы»).
Синтаксис:
=ЧАСТОТА(Массив_Данных; Массив_интервалов)
· Массив_Данных – массив или ссылка на множество ЧИСЛОвых данных, для которых вычисляются частоты;
· Массив_Интервалов - массив или ссылка на множество интервалов, в которые группируются значения аргумента «Массив_Данных».
· Замечания:
1. Функция игнорирует пустые ячейки и ячейки с текстом, т.е. работает только с числами.
2. Для использования функции ЧАСТОТА нужно:
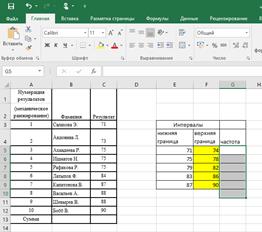
1) заранее подготовить ячейки с интересующими нас интервалами-карманами (на рис. 2.16. это диапазон F5:F9 )
2) выделить пустой диапазон ячеек (G5:G10) по размеру на одну ячейку больший, чем диапазон карманов (F5:F9), в дополнительной ячейке будет содержаться количество значений, превышающих верхнюю границу интервала, содержащего наибольшие значения (рис. 2.16).
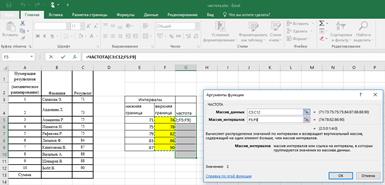
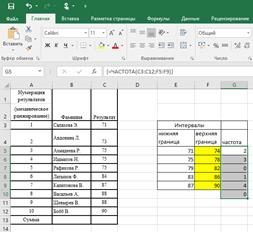
3) ввести функцию ЧАСТОТА и нажать в конце сочетание Ctrl+Shift+Enter, т.е. ввести ее как формулу массива (рис. 2.17, 2.18).
|
| Рис. 2.16. Подготовка ячеек к вводу функции ЧАСТОТА |
|
| Рис. 2.17. Аргументы функции ЧАСТОТА |
|
| Рис. 2.18. Результаты, полученные с помощью функции ЧАСТОТА |
2.7.2. Включение блока инструментов «Анализ данных» в M S Excel
|
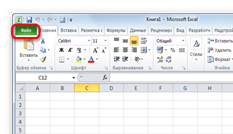
| Рис. 2.19. Вкладка «Файл» |
|
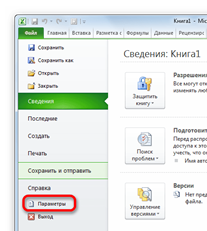
| Рис. 2.20. Пункт «Параметры» |
Программа Excel – это не просто табличный редактор, но ещё и мощный инструмент для различных математических и статистических вычислений. В приложении имеется огромное число функций, предназначенных для этих задач. Правда, не все эти возможности по умолчанию активированы. Именно к таким скрытым функциям относится набор инструментов «Анализ данных».
Чтобы воспользоваться возможностями, которые предоставляет функция «Анализ данных», нужно активировать группу инструментов «Пакет анализа», выполнив определенные действия в настройках Microsoft Excel. Алгоритм этих действий практически одинаков для версий программы 2010, 2013 и 2016 года, и имеет лишь незначительные отличия у версии 2007 года.
Активация
Шаг 1. Перейти во вкладку «Файл» (рис.2.19). Если используется версия Microsoft Excel 2007, то вместо кнопки «Файл» нажать значок Microsoft Office в верхнем левом углу окна.
Шаг 2. Кликнуть по одному из пунктов, представленных в левой части открывшегося окна – «Параметры» (рис. 2.20).
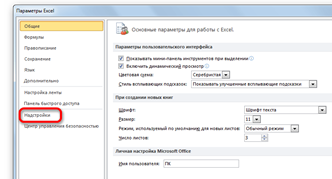
Шаг 3. В открывшемся окне «Параметры Excel » перейти в подраздел «Надстройки» (предпоследний в списке в левой части экрана) (рис. 2.21).
|
| Рис. 2.21. Подраздел «Надстройки» |
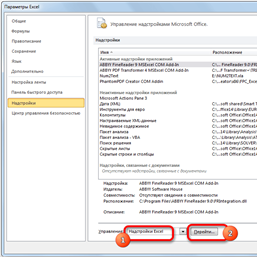
Шаг4. В подразделе «Надстройки» представлен параметр «Управление». Если в выпадающей форме, относящейся к нему, стоит значение отличное от «Надстройки Excel», то нужно изменить его на указанное. Если же установлен именно этот пункт, то просто кликнуть на кнопку «Перейти…» справа от него (рис. 2.22).
|
| Рис. 2.22. Параметр «Управление» |
|
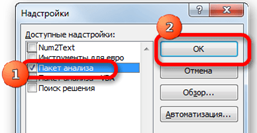
Рис. 2.23. «Пакет анализа»
|
| Рис.2.24. Вкладка «Данные» |
Шаг5. Откроется небольшое окно доступных надстроек. Среди них нужно выбрать пункт «Пакет анализа» и поставить около него галочку. После этого, нажать на кнопку «OK», расположенную в самом верху правой части окошка (2.23).
После выполнения этих действий указанная функция будет активирована, а её инструментарий доступен на ленте Excel.
ВОПРОСЫ И УПРАЖНЕНИЯ
1. Дайте определение следующим понятиям: группировка данных, ранжирование, ранг, частота, частость, статистический и вариационный ряды, распределение, гистограмма, полигон распределения и сглаженная кривая.
2. Следующие данные представляют собой оценки 75 взрослых людей в тесте на определение коэффициента интеллектуальности Стенфорда-Бине:
| 141 | 104 | 101 | 130 | 148 |
| 92 | 87 | 115 | 96 | 91 |
| 100 | 133 | 124 | 123 | 92 |
| 132 | 118 | 98 | 107 | 101 |
| 97 | 124 | 118 | 107 | 146 |
| 110 | 111 | 138 | 129 | 121 |
| 106 | 135 | 97 | 108 | 108 |
| 107 | 110 | 101 | 105 | 129 |
| 105 | 110 | 116 | 123 | 113 |
| 83 | 127 | 112 | 105 | 114 |
| 127 | 114 | 113 | 139 | 106 |
| 95 | 105 | 95 | 106 | 105 |
В задаче:
· сгруппируйте результаты наблюдений;
· определите частоту и частость показателей;
· выберите интервал группирования разрядов;
· постройте распределение сгруппированных частот, полигон распределения и сглаженную кривую.
3. Проведите ранжирование следующих результатов наблюдений: 10, 12, 11, 13, 12, 7, 8, 6, 11, 8, 12, 14, 11.
Лабораторная работа №1
Представление данных
Задание 1. Данные статистического ряда упорядочить (сортировать) и проранжировать.
Задание 2. Определить оптимальное количество интервалов, ширину интервалов, разбить ряд на интервалы, найти середину каждого интервала, частоту и частость показателей в интервалах, построить гистограмму и полигон распределения.
| | ||||||||||
Варианты
| |
Варианты | |||||||||
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | |
| x1 | 15 | 16 | 10 | 12 | 13 | 13 | 14 | 14 | 15 | 15 |
| x 2 | 15 | 15 | 9 | 12 | 12 | 1 | 14 | 14 | 15 | 15 |
| x 3 | 11 | 11 | 7 | 8 | 8 | 9 | 9 | 9 | 11 | 10 |
| x 4 | 6 | 6 | 11 | 3 | 3 | 4 | 5 | 6 | 6 | 5 |
| x5 | 8 | 8 | 5 | 5 | 5 | 5 | 7 | 6 | 8 | 7 |
| x6 | 12 | 12 | 5 | 9 | 9 | 9 | 11 | 11 | 12 | 11 |
| x7 | 6 | 6 | 11 | 3 | 3 | 4 | 5 | 14 | 6 | 6 |
| x8 | 6 | 7 | 15 | 3 | 4 | 4 | 5 | 5 | 6 | 6 |
| x9 | 12 | 12 | 9 | 12 | 9 | 10 | 11 | 11 | 12 | 12 |
| x10 | 12 | 16 | 12 | 15 | 12 | 13 | 14 | 11 | 15 | 15 |
| x11 | 14 | 14 | 11 | 13 | 11 | 11 | 12 | 12 | 13 | 13 |
| x12 | 2 | 2 | 3 | 3 | 3 | 4 | 4 | 5 | 5 | 3 |
| x13 | 13 | 11 | 10 | 12 | 10 | 10 | 8 | 8 | 12 | 12 |
| x14 | 12 | 13 | 10 | 12 | 8 | 11 | 7 | 11 | 12 | |
| x 1 5 | 10 | 10 | 4 | 13 | 1 | 2 | 11 | 12 | 12 | 13 |
| x 1 6 | 13 | 13 | 11 | 12 | 11 | 6 | 11 | 2 | 12 | |
| x 1 7 | 10 | 10 | 9 | 10 | 13 | 2 | ||||
| x 1 8 | 2 | 9 | 6 | 6 | ||||||
Мода
Мода ( Mo )– это значение во множестве наблюдений, которое встречается наиболее часто.
Задача 3.1. В совокупности значений (1, 2, 2, 7, 8, 8, 8, 10) найти моду.
Так как значение 8 встречается чаще любого другого значения, то 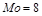 .
.
Однако не всякая совокупность значений имеет единственную моду в строгом понимании этого определения, поэтому рабочее определение моды содержит особенности и соглашения.
1. Если все значения в группе встречаются одинаково часто, то группа оценок не имеет моды. Так, в группе
0,2; 0,2; 2,3; 2,3; 4,1; 4,1
моды нет.
2. Если два соседних значения имеют одинаковую частоту, и они больше частоты любого другого значения, то мода есть среднее этих двух значений. Итак, мода группы значений
0,1, 1, 2, 2, 2, 3, 3, 3, 4
равна
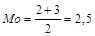 .
.
3. Если два несмежных значения в группе имеют равные частоты, и они больше частот любого значения, то существуют две моды. Например, в группе значений
5, 7, 7, 7, 10, 11, 12, 12, 12, 17
модами являются 7 и 12. В таком случае говорят, что группа оценок является бимодальной.
Замечание. Большие множества данных часто рассматриваются как бимодальные, когда они образуют полигон частот, похожий на спину бактриана (двугорбый верблюд), даже если частоты на двух вершинах не строго равны. Это незначительное искажение определения вполне оправданно, ибо термин «бимодальный» допустим и удобен для описания. Можно условиться различать большие и меньшие моды.
Наибольшей модой в группе называется единственное значение, которое удовлетворяет определению моды. Однако во всей группе может быть и несколько меньших мод. Эти меньшие моды представляют собой, в сущности, локальные вершины распределения частот.
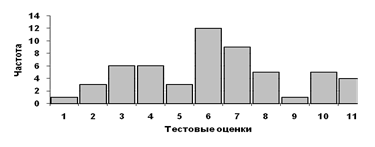
Например, на рисунке 3.1 1.7 наибольшая мода наблюдается при значении 6, а меньшие – при 3,5 и 10.
|
| Рис. 3.1. Распределение частот тестовых оценок с наибольшей модой 6 и меньшими модами 3,5 и 10 |
МЕДИАНА
Медиана (Mе) – значение, которое делит упорядоченное множество данных пополам, так что одна половина значений оказывается больше медианы, а другая – меньше.
Вычисление медианы:
1. Если данные содержат нечетное число различных значений, то медиана есть среднее значение для случая, когда они упорядочены. Например, в группе
17, 19, 21, 24, 27 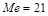 .
.
2. Если данные содержат четное число различных значений, то медиана есть точка, лежащая посредине между двумя центральными значениями, когда они упорядочены. В группе
3, 11, 16, 20 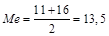 .
.
3. Если в данных есть объединенные классы, особенно в окрестности медианы, возможно, потребуется табулирование частот. В таких случаях придется интерполировать внутри разряда значений.
Задача 3.2. Пусть, например, 36 значений, упорядоченных от 7,0 до 10,5, имеют следующее распределение:
| Значение | Частота | Накопленная частота |
| 10,5 | 2 | 36 |
| 10,0 | 3 | 34 |
| 9,5 | 2 | 31 |
| 9,0 | 6 | 29 |
| 8,5 | 10=5+5 | 23 |
| 8,0 | 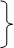 8 8
| 13 |
| 7,5 | 4 13 | 5 |
| 7,0 | 1 | 1 |
| n=36 |
Оценкой медианы будет величина n/2, равная 18-му значению снизу. Медиана будет находиться по формуле:
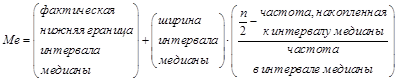 (3.1)
(3.1)
§ фактическая нижняя граница интервала равна 8,25;
§ ширина интервала медианы равна 0,5;
§ оценка медианы 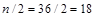 ;
;
§ частота, накопленная к интервалу медианы, равна13;
§ частота в интервале медианы равна 10.
Подставляя найденные значения в формулу (3.1), получим:
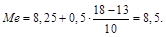
СРЕДНЕЕ
Среднее (среднее выборочное, арифметическое среднее, математическое ожидание) выборочной совокупности п различных значений определяется как
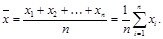 (3.2)
(3.2)
Если даны значения и частоты их повторения, то среднее значение определяется формулой:
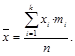 (3.3)
(3.3)
Задача 3.3. Найти среднее для значений из задачи 3.2:
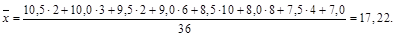
Если даны значения в интервале, тогда за xi берутся середины интервалов.
Соответствующим параметром генеральной совокупности будет средняя генеральной совокупности m, которая вычисляется по формуле (3.4), аналогичной формуле (3.2):
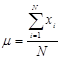 , (3.4)
, (3.4)
где 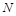 – численность или объем генеральной совокупности.
– численность или объем генеральной совокупности.
Свойства среднего:
1. Сумма всех отклонений от среднего значения равна нулю:
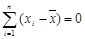 . (3.5)
. (3.5)
2. Если константу прибавить к каждому значению, то среднее увеличится ровно на эту константу:
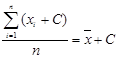 . (3.6)
. (3.6)
3. Если каждое значение умножить на константу с, то среднее увеличится в с раз:
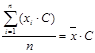 . (3.7)
. (3.7)
4. Сумма квадратов отклонений значений от их среднего значения меньше суммы квадратов отклонений от любой другой точки:
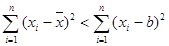 . (3.8)
. (3.8)
ВОПРОСЫ И УПРАЖНЕНИЯ
1. Дайте определение моде, медиане и среднему значению.
2. Найдите среднее, медиану и моду следующих множеств:
§ 2, 7, 4, 5, 2;
§ 3, 1, 0, 7, 2, 6, 2, 6;
§ 1, 7, 3, 8, 3, 3, 9, 11, 9, 12, 9, 12, 13
§ 22, 15, 16, 21, 24, 24, 27, 28, 30, 30, 31, 31, 31, 34, 36.
3. Пусть к каждому из 15 значений последнего множества из упражнения 2 прибавлено 4. Чему будут равны среднее и медиана этих увеличенных значений?
4. В классе А – 10 учащихся, среднее и медиана результатов контрольной работы равны соответственно 4,2 и 4. В классе Б – 20 учащихся, среднее и медиана результатов контрольной работы которых равны 4,3 и 4,5 соответственно. Чему равны среднее и медиана 30 значений, полученных в результате объединения оценок в классах А и Б?
5. На какую меру центральной тенденции влияют значения всех результатов?
Тема 4. Числовые характеристики распределения данных. Мера рассеивания
Используя для описания ряда значений признака, только меру центральной тенденции, можно сильно ошибиться в оценке характера изучаемой совокупности. Это хорошо видно на следующем примере.
Пример. Пусть изучается средний возраст в двух группах, состоящих каждая из 6-ти человек. Значения признака распределились следующим образом:
1 группа – 10, 10, 10, 50, 50, 50;
2 группа – 30, 30, 30, 30, 30, 30.
Подсчитав среднее значение в каждой из групп, получим:
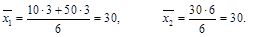
То есть мы получили одинаковые значения, тогда как совершенно очевидно, что выборки взяты из разных совокупностей. Ошибка произошла из-за разброса значений возраста в этих группах.
Существует несколько способов оценки степени рассеивания или разброса данных. Основными характеристиками рассеивания являются: размах, дисперсия, среднеквадратическое (стандартное) отклонение, коэффициент вариации
РАЗМАХ
Размах R (разброс выборки) – разность между максимальным и минимальным значениями вариационного ряда.
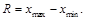 (4.1)
(4.1)
Размах измеряет на числовой шкале расстояние, в пределах которого изменяются оценки. Это самый простой показатель, который можно получить для выборки.
Понятно, что чем сильнее варьирует измеряемый признак, тем больше величина R, и наоборот. Однако может случиться так, что у двух выборочных рядов и средние, и размах совпадают, однако характер варьирования этих рядов будет различный. Для того, чтобы более четко представлять характер варьирования выборок, следует обратиться к их распределениям
Мода
Для нахождения моды в старых версиях Excel существовала функция МОДА, но в более поздних она была разбита на две:
1) МОДА.ОДН (для отдельных чисел);
2) МОДА.НСК(для массивов).
=МОДА.ОДН(число1;число2;…)
=МОДА.НСК(число1;число2;…)
Медиана
Для вычисления медианы применяется функция МЕДИАНА, которая устанавливает не среднее арифметическое, а просто среднюю величину между наибольшим и наименьшим числом области значений. Синтаксис выглядит так:
=МЕДИАНА(число1;число2;…)
Среднее
Для определения среднего значения используется функция СРЗНАЧ, которая ищет число в указанном диапазоне, ближе всего находящееся к среднему арифметическому значению. Результат этого расчета выводится в отдельную ячейку, в которой и содержится формула. Шаблон у неё следующий:
=СРЗНАЧ(число1;число2;…)
Дисперсия
В MS Excel 2007 и более ранних версиях для вычисления дисперсии выборки используется функция ДИСП(). С версии MS Excel 2010 рекомендуется использовать ее аналог ДИСП.В(). Кроме того, начиная с версии MS Excel 2010 присутствует функция ДИСП.Г(), которая вычисляет дисперсию для генеральной совокупности. До MS Excel 2010 для вычисления дисперсии генеральной совокупности использовалась функция ДИСПР().
Отличие в вычислении выборочной и генеральной совокупности сводится к знаменателю в формулах (4.2) и (4.4).
Стандартное отклонение
В Excel используются несколько вариантов этой функции отклонения:
§ Функция СТАНДОТКЛОНА – вычисляется отклонение по выборке текстовых и логических значений. При этом ложные логические и текстовые значения формула приравнивает к 0, а 1 будут равняться только истинные логические значения;
§ Функция СТАНДОТКЛОН.В – производит оценку стандартного отклонения по выборке, при этом текстовые и логические значения игнорирует;
§ Функция СТАНДОТКЛОН.Г – делает оценку отклонения по некой генеральной совокупности и как в предыдущей функции игнорируются текстовые и логические значения;
§ Функция СТАНДОТКЛОНПА – также вычисляет по генеральной совокупности стандартное отклонение, но с учетом текстовых и логических значений. Равняться 1 будут только истинные логические значения, а ложные логические и текстовые значения будут приравнены к 0.
Коэффициент вариации
Для расчета коэффициента вариации в Excel нет готовой функции. Однако, расчет можно произвести простым делением стандартного отклонения на среднее значение. Для этого в строке формул пишем:
=СТАНДОТКЛОН.Г()/СРЗНАЧ()
В скобках указывается диапазон данных. При необходимости используют среднее квадратичное отклонение по выборке (СТАНДОТКЛОН.В).
Коэффициент вариации обычно выражается в процентах, поэтому ячейку с формулой можно обрамить процентным форматом. Нужная кнопка находится на ленте на вкладке «Главная».
Задача 4.2. У студентов первого и второго курса был исследован уровень депрессивного расстройства по методике Бэка. Сделать сравнительный анализ, используя методы описательной статистики. Результаты тестирования даны в таблице 4.2.
Таблица 4.2
| 1 курс | 2 курс |
| 30 | 24 |
| 27 | 17 |
| 23 | 17 |
| 22 | 17 |
| 19 | 17 |
| 19 | 14 |
| 18 | 14 |
| 16 | 13 |
| 15 | 12 |
| 14 | 12 |
| 13 | 11 |
| 12 | 11 |
| 12 | 8 |
| 12 | 8 |
| 10 | 7 |
| 10 | 7 |
| 10 | 4 |
| 10 | 0 |
1. С помощью статистических функций MS Excel найдем оценку центральной тенденции:
Таблица 4.3
|
| 1 курс | 2 курс |
| мода | 10 | 17 |
| медиана | 14,5 | 12 |
| среднее | 16,2 | 11,8 |
Медиана и среднее арифметическое значение на первом курсе выше, чем на втором, из чего можно сделать вывод, что уровень депрессивного расстройства на 1 курсе превышает уровень расстройства на втором курсе. Однако мода на 2-ом курсе значительно выше, чем на первом, т.е. преобладают более высокие значения уровня депрессивного расстройства.
2. Произведем оценку разброса данных:
Таблица 4.4
|
| 1 курс | 2 курс |
| дисперсия | 37,0 | 32,0 |
| ст. отклонение | 6,1 | 5,7 |
| коэффициент вариации | 37,5% | 47,8% |
Коэффициент вариации и на 1-ом курсе и на 2-ом выше 33%, что говорит о неоднородности данных в этих группах. Однако, дисперсия и стандартное отклонение на 1-ом курсе выше, чем на 2-ом, что говорит о более широком разбросе данных и следовательно, можно сделать вывод о том, что вторая выборка более однородна.
ВОПРОСЫ И УПРАЖНЕНИЯ
1. Дайте определение размаху, выборочной дисперсии, генеральной дисперсии, стандартному отклонению. Воспроизведите формулы для их нахождения.
2. Что характеризует выборочная дисперсия.
3. Вычислите для множества: 22, 15, 16, 21, 24, 24, 27, 28, 30, 30, 31, 31, 31, 34, 36 размах, дисперсию, стандартное отклонение.
4. В каких случаях можно проводить сравнение разных выборок по дисперсиям?
5. Выборочные дисперсии результатов контрольной работы в классе 7«А» и 7«Б» соответственно равны 0,44 и 1,38. Какой вывод можно сделать при сравнении результатов контрольной работы в двух классах?
6. Дисперсия каждой из групп A и В равна 5. Будет ли дисперсия 10 значений, полученных путем объединения групп, меньше, больше или равна 5?
Группа А: 13, 11, 10, 9, 7
Группа В: 28, 26, 25, 24, 22
Лабораторная работа №2
Описательная статистика
Этапы обработки данных:
1. Занести данные в таблицу Excel (две выборки).
2. Упорядочить данные (по возрастанию) в каждой выборке.
3. Рассчитать моду, медиану и среднее.
4. Посчитать дисперсию, стандартное отклонение.
5. Посчитать коэффициент вариации.
6. Сделать сравнительный анализ, полученных результатов.
Задания для вариантов 1 – 5
При определении степени выраженности некоторого психического свойства в двух группах, опытной и контрольной, баллы распределились следующим образом.
Дать сравнительную характеристику степени выраженности этого свойства в данных группах.
Вариант 1.
| Опытная | 18, 15, 16, 11, 14,15, 16, 16, 20, 22, 17, 12, 11, 12, 18, 19, 20 |
| Контрольная | 26, 8, 11, 12, 25, 22, 13, 14, 21, 20, 15, 16, 17, 16, 9, 11, 16 |
Вариант 2
| Опытная | 19, 16, 17, 12, 15,16, 17,17, 21, 23, 18, 13, 12, 13, 19, 20, 21 |
| Контрольная | 27, 9, 12, 13, 26, 23, 14, 15, 22, 21, 16, 16, 18, 17, 10, 12, 17 |
Вариант 3.
| Опытная | 16, 13, 14, 9, 10,13, 14,14, 18, 20, 15, 10, 9, 10, 16, 17, 18 |
| Контрольная | 24, 6, 9, 10, 23, 20, 11, 12, 19, 18, 13, 14, 12, 14, 7, 9, 14 |
Вариант 4.
| Опытная | 15, 12, 13, 8, 11,12, 13,13, 17, 19, 14, 9, 8, 9, 15, 16, 17 |
| Контрольная | 23, 5, 9, 9, 22, 19, 10, 11, 18, 17, 12, 13, 14, 13, 6, 8, 13 |
Вариант 5.
| Опытная | 15, 12, 13, 8, 11,12, 13,13, 17, 19, 14, 9, 8, 9, 15, 16, 17 |
| Контрольная | 24, 6, 9, 10, 23, 20, 11, 12, 19, 18, 13, 14, 12, 14, 7, 9, 14 |
Задания для вариантов 6 – 10
Была исследована группа детей с заболеванием крови до лечения препаратами и после лечения. В таблицу занесены показатели крови по результатам медицинского обследования. Сделать сравнительный анализ результативности лечения данным препаратом, используя методы описательной статистики.
Вариант 6.
| до лечения | 20,5 12,1 13,6 40,5 9,6 33 77,2 8,7 3,5 13,8 7,4 29,4 116 21,9 |
| после лечения | 2,3 7,5 3,8 3,8 8,8 13 4,7 3,9 4,8 5,7 9 13 0,9 |
Вариант 7.
| до лечения | 280 230 100 60 90 80 8 36 50 90 17 42 42 30 |
| после лечения | 86 280 30 170 210 230 230 156 102 161 15 60 20 |
Вариант 8.
| до лечения | 112 60 84 60 60 40 76 60 84 40 112 46 64 70 |
| после лечения | 82 78 110 130 130 104 108 129 110 88 105 73 85 80 |
Вариант 9.
| до лечения | 113 61 85 61 61 41 77 61 85 41 113 47 65 71 |
| после лечения | 81 77 109 129 129 103 107 128 109 87 104 72 84 79 |
Вариант 10.
| до лечения | 111 59 83 59 59 39 75 59 83 39 111 45 63 69 |
| после лечения | 83 79 111 131 131 105 109 130 111 89 106 74 86 81 |
Задания для вариантов 11 – 15
Для проверки эффективности новой развивающей программы были созданы две группы детей шестилетнего возраста. На первом этапе дети обеих групп были протестированы по методике Керна-Йерасика (школьная зрелость). Результаты тестирования по невербальной шкале занесены в таблицу. Сделать сравнительный анализ школьной зрелости детей этих групп.
Вариант 11.
| Эксперимент. | 29 31 31 25 25 19 22 20 14 16 27 24 32 27 14 24 |
| Контроль | 34 31 28 27 30 23 21 28 29 31 17 22 21 15 33 29 |
Вариант 12.
| Эксперимент. | 14 13 11 8 12 13 13 13 11 12 14 13 12 14 10 13 |
| Контроль | 13 13 14 12 14 14 12 13 15 13 11 12 14 9 14 13 |
Вариант 13.
| Эксперимент. | 33 33 37 33 34 33 31 29 29 35 31 29 31 34 26 26 |
| Контроль | 39 30 38 36 31 37 35 32 39 34 30 32 36 29 39 36 |
Вариант 14.
| Эксперимент. | 13 12 10 7 11 12 12 12 10 11 13 12 11 13 9 12 |
| Контроль | 12 12 13 11 13 13 11 12 14 12 10 11 13 8 13 12 |
Вариант 15.
| Эксперимент. | 30 32 32 26 26 20 23 21 15 17 28 25 33 28 15 25 |
| Контроль | 35 32 29 28 31 24 22 29 30 32 18 24 22 16 34 30 |
Задания для вариантов 16 – 20
У участников психологического исследования, в число которых входила группа педагогов и группа непедагогов, был исследован уровень конфликтности. Полученные данные занесены в таблицу. Можно ли утверждать, что уровень конфликтности педагогов выше, чем у непедагогов?
Вариант 16.
| Педагоги | 32 31 32 29 32 28 32 32 25 39 29 31 35 32 26 31 20 33 22 30 |
| Непедагоги | 24 25 25 24 30 27 28 28 30 30 31 29 30 24 33 32 35 |
Вариант 17.
| Педагоги | 31 30 31 28 31 27 31 31 24 38 28 30 34 31 25 30 19 32 21 29 |
| Непедагоги | 23 24 24 23 29 28 27 27 29 29 30 28 29 23 32 31 34 |
Вариант 18.
| Педагоги | 33 32 33 30 33 29 33 33 26 40 30 32 36 33 27 32 21 34 23 31 |
| Непедагоги | 25 26 26 25 31 28 29 29 31 31 32 30 31 25 34 33 36 |
Вариант 19.
| Педагоги | 36 41 41 41 41 40 37 39 35 39 40 45 45 42 42 45 41 36 34 40 39 |
| Непедагоги | 35 38 38 33 41 41 44 38 36 42 43 38 40 35 37 48 46 |
Вариант 20.
| Педагоги | 35 40 40 40 40 39 36 38 34 38 39 44 44 41 41 44 40 35 33 39 38 |
| Непедагоги | 34 37 37 32 40 40 43 37 35 41 42 37 39 34 36 47 45 |
РАЗДЕЛ 1. МЕТОДЫ ОПИСАТЕЛЬНОЙ СТАТИСТИКИ
Тема1. Выборочный метод
Дата: 2018-11-18, просмотров: 6277.