Характеристик гребного винта с использованием
Судовой документации
Теоретическая часть
Знакомясь с общими сведениями о судовых движителях, следует уяснить принцип действия гидравлических движителей, так как они находят наибольшее распространение на судах.
Изучая геометрию винтов, необходимо помнить, что все геометрические характеристики винта даются для его нагнетающей поверхности. Нужно твердо усвоить основные геометрические параметры винта: шаг, шаговый угол, дисковое отношение и уметь их определить на практике. Взаимодействие ГВ с корпусом судна (попутный поток, засасывание, пропульсивный коэффициент). Взаимосвязь между работой ГВ и двигателя. Кавитация гребных винтов. Конструкция винтов регулируемого шага.
Примеры решения типовых задач
Задача № 21.1
Найти шаговое отношение винта постоянного шага диаметром 5,0 м, если на r = 0,7R шаговый угол φ =200.
Решение:
Для винта постоянного шага, шаг винта в любой точке нагнетающей поверхности неизменен.
Шаг винта: H = 2π r tg φ = 2·3,14·1,75· tg 200= 4 м.
Шаговое отношение: H/D = 4/5 = 0,8
Задача № 21.2
Найти шаг винта радиально- переменного шага диаметром 5,2 м, на r = 0,3 R, если шаговые уголы φ =400.
Решение:
Шаг винта определяется:
H = 2π r tg φ = 2·3,14·0,78· tg 400= 4,11 м.
Задача № 21.3
Определть шг винта постоянного шага, если при центральном угле α=100 , подъем винтовой линии h = 20 см.
Решение:
В данном случае шаг винта определяется как подъем винтовой линии за один оборот:
Н = h·3600 /α0 = 0,2·36 =7,2 м.
Задание
На практическом занятии необходимо решить задачи из § 10.7 задачника [3]. Основные зависимость и примеры решения типовых задач в § 10.1-10.6, [3]. Номера задач и их количество определяет преподаватель.
Вопросы для самоконтроля
1. В чем состоит принцип действия гребных винтов?
2. Что называется дисковым отношением?
3. Какое преимущество имеют авиационные лопастные сечения по сравнению с сегментными?
4. С какой частотой вращения должен работать главный двигатель на буксируемом судне, чтобы гребной винт с шагом нулевого упора H1 = 6,5 м не создавал упора. Скорость буксировки соответствует υp = 5 м/с.
Литература: [1] стр. 208-241,
[3] стр. 102-119,
[4] стр. 120-144
ПрактическОЕ ЗАНЯТИЕ №22
Общие сведения. Местная и общая прочность корпуса. Определение изгибающих моментов и перерезывающих сил
Теоретическая часть
Целью изучения темы является ознакомление обучающихся с вопросами прочности корпуса судна, а также корпусными конструкциями промысловых судов.
Для лучшего усвоения материала необходимо повторить плоский изгиб балок, обратив внимание на дифференциальные зависимости между внешней нагрузкой, перерезывающими силами и изгибающими моментами, а также на вычисление нормальных и касательных усилии.
Примеры решения типовых задач
Задача № 22.1
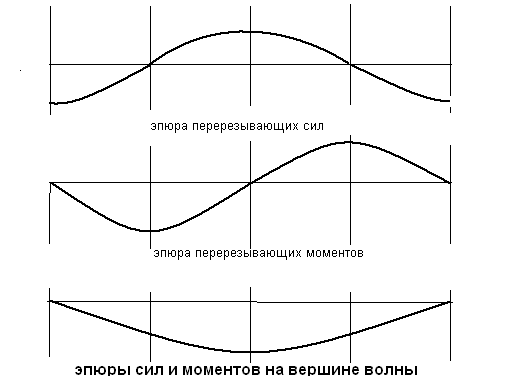
Построить эпюры дополнительных перерезывающих сил и изгибающих моментов для прямоугольного понтона при положении его на вершине и подошве волны. Профиль волны принять синусоидальным. Ширина понтона 10 метров, высота волны h = 0,17 L 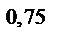 ; вода пресная; длина волны равна длине понтона L = 70 м.
; вода пресная; длина волны равна длине понтона L = 70 м.
Решение:
Дополнительные перерезывающие силы при статической постановке на волну
δ N(x) = ρg 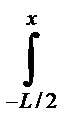 δw dx
δw dx
где: ρ - массовая плотность воды
g - ускорение свободного падения
δw - изменение площади шпангоута
dx - изменение осадки по длине судна
Изменение осадки понтона при постановке на вершине волны
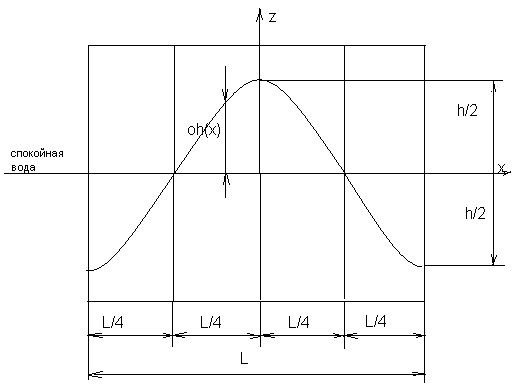
Δh = h 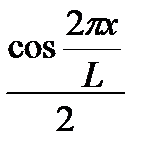 =
= 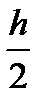 cos
cos 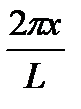
Так как случай постановки понтона на подошве волны является симметричным относительно ватерлинии на спокойной воде, то на подошве волны
Δh = - 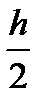 cos
cos 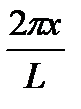 следовательно
следовательно
Δh = 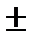
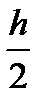 cos
cos 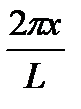 где (+) на подошве волны
где (+) на подошве волны
(-) на вершине волны
тогда δw = 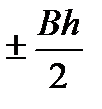 cos
cos 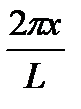
δ N(x) = 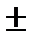 ρg
ρg 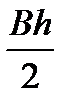
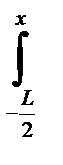 cos
cos 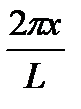 dx =
dx = 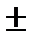 ρg
ρg 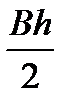
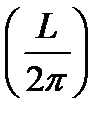 sin
sin 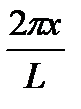
Дополнительные изгибающие моменты при этом
δ М(x) = 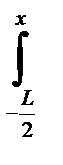 δ N(x ) dx =
δ N(x ) dx = 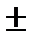 ρg
ρg 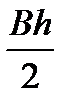
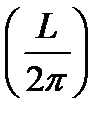
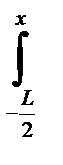 sin
sin 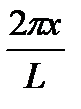 dx =
dx =
= 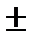 ρg
ρg 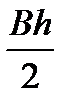
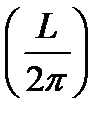
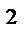 ( cos
( cos 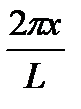 + 1)
+ 1)
а) случай на подошве волны
δ N(x)max = δ N 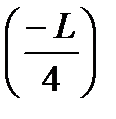 = - ρg
= - ρg 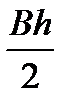
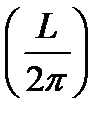 sin
sin 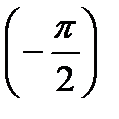 = 2250 Кн
= 2250 Кн
δ N(x)min = δ N( L /4) = 2250 Кн
δ М(x)max = 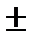 ρg
ρg 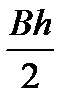
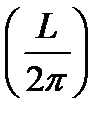
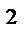 = 1000*9,81*10*4,11*(
= 1000*9,81*10*4,11*( 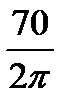 )
) 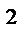 = 50000 Кн
= 50000 Кн
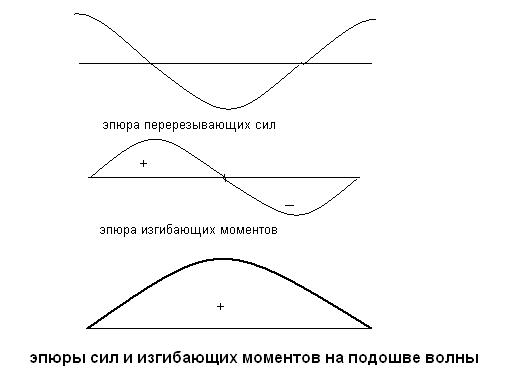
б) случай на вершине волны
δ N(x)max = δ N 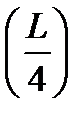 = ρg
= ρg 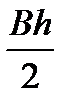
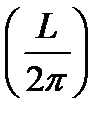 sin
sin 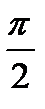 = 2250 Кн
= 2250 Кн
δ N(x)min = δ N(- L /4) = -2250 Кн
δ М(x) min = - ρg 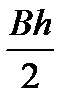
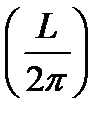
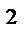 = - 1000*9,81*10*4,11*(
= - 1000*9,81*10*4,11*( 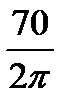 )
) 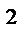 = - 50000 Кн
= - 50000 Кн
δ М(x)max = δ М( 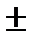 L/2) = 0
L/2) = 0
Задание
На практическом занятии необходимо решить задачи из § 11.3 задачника [3]. Основные зависимость и примеры решения типовых задач в § 11.1-11.2, [3]. Номера задач и их количество определяет преподаватель.
Вопросы для самоконтроля
1. Чем отличается эквивалентный брус от простой балки?
2. Почему при вычислении нормальных напряжений от общего продольного изгиба корпуса применяется метод последовательных приближений?
3. Провести сравнительный анализ поперечной и продольной системы набора.
4. На каких судах выгодно использовать комбинированную систему набора?
Литература: [3] стр. 145-153,
[4] стр.242-257.
ПрактическОЕ ЗАНЯТИЕ №23
Дата: 2018-11-18, просмотров: 1004.