Теоретическая часть

Целью данной работы является, ознакомить курсантов с основными составляющими сопротивления и выявить влияние различных факторов на их величину.   

При изучении составляющих буксировочного сопротивления обучающийся должен обратить внимание на одинаковую структуру формул для их подсчета, так как формулы построены на реновации общего закона механического подобия. Рассматри­вая сопротивление трения, формы и волновое, следует проана­лизировать их зависимость от скорости судна. Нетрудно убе­диться, что вязкостные составляющие буксировочного сопротив­ления изменяются примерно пропорционально квадрату скорости хода, а волновое сопротивление зависит от скорости в более высоких степенях.

При рассмотрении составляющих сопротивления необходимо уяснить физическую сущность явлений, в особенности это касается сопротивления формы и волнового.

Изучение экспериментального определения сопротивления имеет большое значение для понимания современных методов его расчета.

Необходимо ясно представлять, почему нельзя при испыта­ниях обеспечить полное динамическое подобие между моделью и судном.       

Главное внимание при рассмотрении приближенных спосо­бов расчета сопротивления следует уделить графикам, построенным по результатам систематических испытаний моделей со­временных промысловых судов.

Изучая режимы быстроходности судов, нужно уяснить, как меняются отдельные составляющие буксировочного сопротив­ления с изменением числа Фруда. С чисто практической точки зрения важен вывод о том, что у большинства промысловых судов основная часть полного сопротивления приходится на со­противление трения.

Примеры решения типовых задач

Задача № 19.1

Определить сопротивление трения двухвинтового пассажирского т/х «Любовь Орлова» с учетом выступающих частей при скорости 17 уз. Данные судна: L =100м; B = 16,22м;d = 4,65м; δ = 0,565.

Решение:

Rf = 0,5 ( ζ f + ζп + ζа)ρ · v 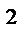· Ω

Число Rе = v· l/υ =0,514·17·100/1,57· 10 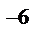= 4,98· 10⁸

Из таблицы находим:

ζ f =1,75·10^-3 ; ζ п = 0,4·10^-3; ζа = 0,6·10^-3  

Площадь смоченной поверхности:

Ω = L· d(1,97 + 1,37(δ – 0,274) 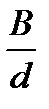) = 1562,7 м²

Тогда: Rf = 0,5(1,75 + 0,4 + 0,6)·10^-3·1,025·1562,7·(17·0,514)² = 162 Кн

Задача № 19.2

Буксир – толкач «Билибино» в тихую погоду транспортирует баржу с лесом со скоростью 9 уз. Данные буксира: L =43,7м; B = 13,5м;d = 4,5м; δ = 0,65; Xc = 0,22 м; Ne = 2· 2200 Квт. Мощность передается к винтам через редуктор, ηд = 0,52. Определить сопротивление толкаемой баржи.

Решение:

Определим объемное сопротивление буксира: V = δ· L· B· d = 1730 м³

Число Rе = v· l/υ =0,514·9·0,514·43,7/1,57· 10 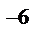= 1.29·10⁸

По рис 9.1 определим коэффициент соротивления трения: ζ f =2,05·10^-3

Из таблицы на стр.103 найдем надбавку на шероховатость ζ п = 0,4·10^-3

По таблице 9.1 найдем коэффициент выступающих частей ζа = 0,4·10^-3

Определяем площадь смоченной поверхности по приближенной формуле В.Л Семеки: Ω = L· d(1,97 + 1,37(δ – 0,274) 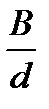) = 691 м²

Сопротивление трения буксира: Rf = 0,5 ( ζ f + ζп + ζа)ρ · v 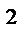· Ω = 21,1 Кн

L/ B = 43,7/13,5 = 3,24; B/ d = 13,5/4,5 = 3;

Число Фруда Fr =v/ 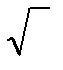9,8·L = 0,223

По рис. 9.4 при Fr и δ определяем ψ0  = 5,85; ζ r = 0,8·10^-3

ψ = L/ 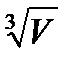 = 3,6

По рис. 9.5 при Fr , ψ0, ψ находим : КB/d  = 1,03

                                                 а B/d  = 1,0

Xc = 100· Xc/ L =100· 0,22/43,7 = 0,503%

По рис 9.7( по Xc и Fr) находим: КXc = 1,0

Коэффициент остаточного сопротивления буксира определяем по формуле: ζ rc  = ζ r·kψ· КB/d · а B/d · КXc = 0,849·10^-3

Остаточное сопротивление: Rr = 0,5 ·ζ rc·  ρ · v 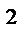· Ω = 6,3 Кн

Буксировочное сопротивление: Nб = (R + R1 ) · v

Откуда буксировочное сопротивление баржи:

R1 = Nб/ v – R

R = Rr + Rf  = 21,1 + 6,3 = 27,4 Кн

Nб = Nе · ηд· ηв· ηп

Где: ηд – кпд гребного винта

   ηв = 0,99 – кпд валопровода

   ηп = 0,98 – кпд передачи
тогда: R1 = Nб/ v – R = Nе · ηд· ηв· ηп/0,514·9 – 27,4 = 213 Кн.

Задание

На практическом занятии необходимо решить задачи из § 9.5 задачника [3]. Основные зависимость и примеры решения типовых задач в § 9.1-9.4, [3]. Номера задач и их количество определяет преподаватель.

Вопросы для самоконтроля

1. Как влияет скорость судна на коэффициенты сопротивле­ния трения, формы и волнового?

2. Почему при испытании моделей не удается обеспечить полное динамическое подобие?

3. Объясните порядок пересчета сопротивления модели на судно.

4. Подсчитайте изменение скорости судна, если мощность его двигателя в результате модернизации увеличилась на 8%.

5. Почему в сильный шторм судно теряет скорость даже при попутном ветре?

Литература: [1] стр. 189-207,

                   [3] стр. 102-119,

                               [4] стр. 149-175.

ПрактическОЕ ЗАНЯТИЕ №20