= h / b = 0,5/1 = 0,5
Угол нулевой подъемной силы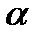 
о = 1,74 
= 1,74 · 0,03 = 0,0522
Где средняя кривизна профиля = f / b = 0,03
Kφ = 1 –(0,5 + δ) exp 
= 0,44
f ( λ / ) = 0,85 + 0,16 
= 0,85 + 0,16 
= 1,49
где λ = l / b = 8 – относительный размах
τ = 0,09 
- 0,04 = 0,214
δ 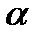о = δ /2(1/ Kφ – 1) = 0,038
Коэффициент подъемной силы при погружении h = 0,5 м. находим по формуле Су = 
= 0,409
Подъемная сила крыла Fyh = Cy·S·ρv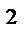 
/ 2 = 0,409·1000·122 ·8 / 2 = 235,6 кН, где S = l · b = 8 м2 – площадь крыла.
Задача № 12.2
Как изменится подъемная сила крыла с относительным размахом λ=6, относительной толщиной δ = 0,05 и 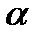+ 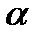0= 0,12 рад, если относительное погружение = 0,4 увеличить до = 0,8?
Решение:
Подъемная сила крыла: Fy = Cy*S*ρv 
/ 2,
где: Cy – безразмерный коэффициент подъемной силы. При изменении относительного погружения меняется только Cy.
Су = 
;
где: Кφ при = 0,4: Кφ = 1 – (0,5 + δ) ехр 
= 0,82,
f( 
λ/ h) = 0,85 + 0,16 
= 0,005;
Кφ при = 0,8: Кφ = 1 – (0,5 + δ) ехр = 0,9.
f( λ/ h) = 0,85 + 0,16 = 0,0027.
τ = 0,09 
- 0,04 = 0,18.
Тогда: при 
= 0,4
Су = = 0,3665;
при = 0,8
Су = =0,4149.
0,4149/0,3665 = 0,132 = 13%.
Таким образом, при изменении относительного погружения до 0,8, подъемная сила увеличится на 13%.
Задача № 12.3
Какова должна быть площадь подводного крыла, движущегося в пресной воде со скоростью 15 м/с при угле атаки 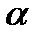= 0,105 рад; f = 0,03; h = 0,1; λ = 0,1; δ = 0,04, чтобы создать подъемную силу 342 Кн.
Решение:
Fy = Cy*S*ρv 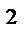/ 2
Коэффициент подъемной силы:
Су = = 0,3872
Где: Кφ = 1 – (0,5 + δ) ехр = 0,6733
f( λ/ h) = 0,85 + 0,16 = 2,2811
τ = 0,09 - 0,04 = 0,2146
δα0 = 
(1/ Кφ – 1) = 9,7 · 10-3
α0 = 1,74 f 
342 = 0,3872·1·152·S/2
Тогда: S = 7,846 м2
Задание
На практическом занятии необходимо решить задачи из § 2.3 задачника [3]. Основные зависимость и примеры решения типовых задач в § 2.1-2.2 [3]. Номера задач и их количество определяет преподаватель.
Вопросы для самоконтроля
1. Что изучает гидромеханика?
2. В чем отличия газообразной среды от капельной жидкости?
3. Что изучает гидростатика?
4. Что такое избыточное (манометрическое давление)?
5. Сформулируйте закон Архимеда.
6. Что изучает гидродинамика?
7. В чем отличия ламинарного движения жидкости от турбулентного?
8. В чем отличие реальной жидкости от идеальной жидкости?
9. Каков смысл критериев Фруда и Рейнольдса?
10. На каком этапе проектирования судна используют положения теории подобия?
11. Назовите основные геометрические характеристики крыла.
Литература: [1] стр.14-26,
………………[3] стр.7-26
[4] стр. 25-34.
ПрактическОЕ ЗАНЯТИЕ №13
Определение параметров посадки судна.
Эксплуатационные расчеты плавучести судна
Теоретическая часть
Целью данной работы является ознакомление обучающихся с методами изображения судовой поверхности. Необходимо поручить четкое представление о плоскостях проекций и способе изображения сечений поверхности корпуса судна. Большое значение для дальнейшего изучения курса имеют главные размерения судна; в частности необходимо четко представлять разницу между длиной судна по ватерлинии и длиной между перпендикулярами. Кроме того, здесь важно уяснить физический смысл коэффициентов полноты, так как с этими понятиями обучающийся будет сталкиваться при изучении всего курса.
На теоретическом чертеже изображены проекции на главные взаимно перпендикулярные плоскости линии пересечения теоретической поверхности корпуса с плоскостями, параллельными главным плоскостям. В качестве главных плоскостей принимают:
- диаметральную плоскость (ДП) - вертикальную продольную плоскость, делящую корпус судна на две симметричные части - правую (правый борт) и левую (левый борт);
- плоскость мидель-шпангоута ( 
) - вертикальную поперечную плоскость, проходящую по середине длины судна и делящую корпус на носовую и кормовую части;
- основную плоскость (ОП) - горизонтальную плоскость, проходящую через нижнюю точку теоретической поверхности корпуса судна в плоскости мидель-шпангоута. Различают две группы главных размерений корпуса судна (рис.3.3) в зависимости от того, связаны они или не связаны с положением ватерлинии:
1) размеры, не связанные с положением судна относительно поверхности воды (чисто конструктивные размеры);
2) размеры, связанные с этим положением и характеризующие деление корпуса судна на надводную и подводную части.
Обводы корпуса судна не воспроизводятся аналитическими зависимостями и заданы графически теоретическим чертежом. Поэтому приведенные интегралы, определяющие элементы погруженного объема судна, не удается вычислить непосредственно.
Для их вычисления используют правила приближенного интегрирования. Из них широкое применение получили три правила - правило трапеций, правило Симпсона и правило Чебышева. При выполнении ручных расчетов наибольшее практическое применение получило правило трапеций.
Посадкой называется положение судна относительно спокойной поверхности воды. Положение действующей ватерлинии относительно корпуса, а значит, и посадку судна в общем случае определяют три параметра:
- d − средняя осадка (осадка на миделе);
- Df − дифферент (разность осадок носом и кормой);
- Θ − угол крена (наклонение судна в вертикально-поперечной плоскости).
Необходимо различать габаритную осадку, которую показывают марки углубления и осадку судна (до основной плоскости).
Примеры решения типовых задач
Задача № 13.1
Каково изменение средней осадки т/х «Новгород» (dср = 9,22м) при переходе из воды плотностью 1,032 т/м3 в воду плотностью 1,02 т/м3.
Решение:
Изменение средней осадки находим по формуле:
δd = (ρ – ρ1) χ d / ρ1 = (1,032 – 1,02) ·0,82 ·9,22/1,02 = 0,089 м.
Где χ = 0,82 - коэффициент вертикальной полноты т/х «Новгород».
Задача № 13.2
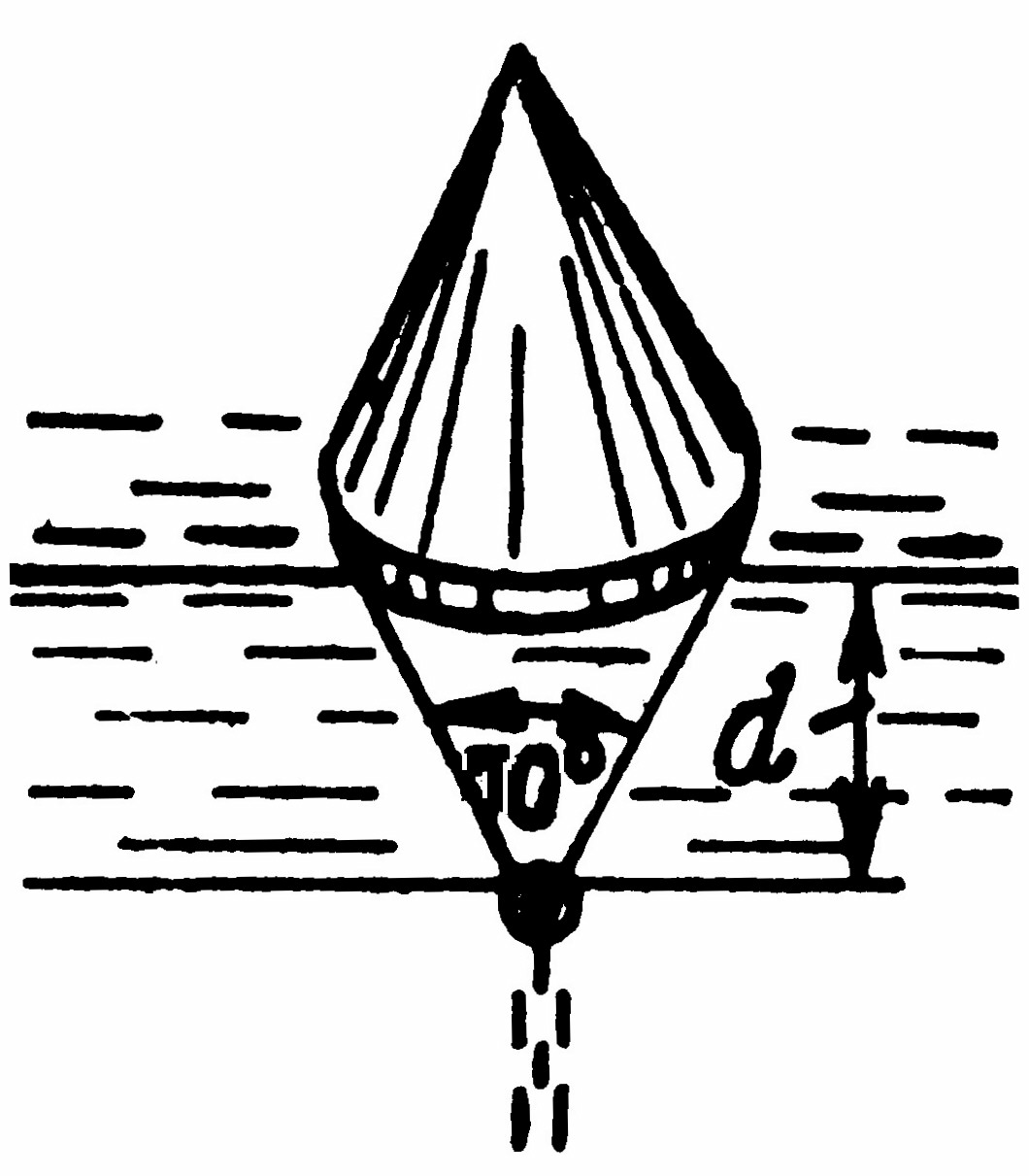
Получить аналитическую зависимость объемного водоизмещения от осадки конусного буя в пределах погружения его от нуля до половины высоты. Чему равна масса буя при высоте 2 м, если в пресной воде d = 6м.
Решение:
Объем конуса: V =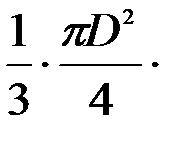 
d = π D2 · d /12,
Где D = 2 d· tg 350 = 1,4 d.
V(d) = π D2 · d /12 = 3,14(1,4 d)2· d/12 = 0,513 d3
Тогда масса буя при d = 0,6 м
M = ρ V = 1,0 · 0,513 · 0,63 = 0,110 т.
Задача № 13.3
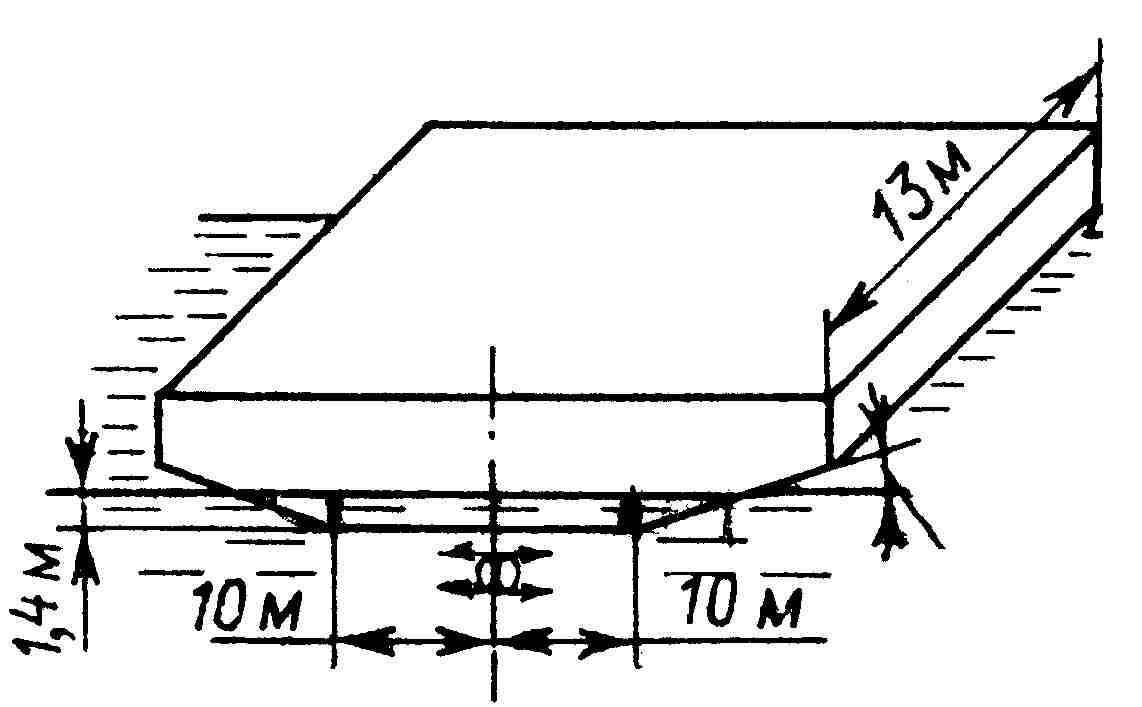
Определить объемное водоизмещение и возвышение Ц.В. понтонов плавучих кранов , формы корпусов которых изображены на рис.
Решение:
Объемное водоизмещение V = А · L = 32,2 ·13 = 418,6 м3 ,
где: А – площадь погруженного в воду мидель-шпангоута:
А = 20 ·1,4 + (1,42/tg 250 ) = 32,2 м2
Задание
На практическом занятии необходимо решить задачи из § 3.3 задачника [3]. Основные зависимость и примеры решения типовых задач в § 3.1-3.2 [3]. Номера задач и их количество определяет преподаватель.
Вопросы для самоконтроля
1. Дайте определения главных плоскостей судна. Как они связаны с координатными плоскостями судна?
2. Что такое батоксы, теоретические шпангоуты и теоретические ватерлинии?
3. Из каких видов состоит теоретический чертеж судна?
4. Где располагаются носовой и кормовой перпендикуляры и номера каких теоретических шпангоутов на них располагаются?
5. Чем отличается конструктивная ватерлиния от действующей ватерлинии?
6. Где используются элементы погруженного объема судна и теоретический чертеж?
7. Назовите основные главные размерения судна.
8. Назовите безразмерные коэффициенты полноты судна и дайте им определения.
9. В чем отличие осадки судна от габаритной осадки?
10. При какой посадке судна можно применять элементы погруженного объема входящие в состав КЭТЧ, а также грузовую шкалу?
11. В каких случаях используют масштаб Бонжана. Как производятся расчеты водоизмещения и координат ЦВ.
Литература: [1] стр.27-49,
………………[3] стр.27-42,
[4] стр. 35-42.
ПрактическОЕ ЗАНЯТИЕ №14
Дата: 2018-11-18, просмотров: 892.
