Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Расчетом посадки и запаса плавучести судна

 

Теоретическая часть

 Целью данной работы является ознакомление с судовой до­кументацией для расчета плавучести судна и методами ее использования. Для лучшего усвоения материала следует повто­рить основные положения гидростатики, определение центра тяжести тел и правила приближенного вычисления интегралов.

Плавучестью называется способность судна плавать в состоянии равновесия в заданном положении относительно поверхности воды при заданной нагрузке.

Силы тяжести приводятся к одной равнодействующей - силе тяжести судна Р, которая направлена вертикально вниз и приложена в центре тяжести судна (ЦТ) - в точке G с координатами x_g , y_g , z_g .

Сила плавучести направлена вертикально вверх и приложена в центре величины судна (ЦВ) - в точке С с координатами x_с, y_с, z_с. Центр величины представляет собой геометрический центр подводного объема судна V, и его положение зависит от формы корпуса судна и его посадки.

При проведении расчетов мореходных качеств, важно знание понятия «малого» и «большого грузов». Эти понятия являются относительными, причем прием большого груза следует рассматривать не как прием крупного тяжеловеса, а как прием нескольких грузов общим весом более 10÷12% от водоизмещения.

Необходимо изучить требования предъявляемые к запасу плавучести Международной конвенцией о грузовой марке 1966г. и Регистром.

Безопасность плавания теснейшим образом связана с нор­мированием и контролем плавучести судов. Поэтому большое значение имеет понимание роли грузовых марок.

При изучении материала нужно хорошо усвоить, что кри­вые элементов теоретического чертежа строятся для судна, си­дящего на ровный киль. Если дифферент судна значителен (более 1÷1,5°), то для определения характеристик плавучести судна следует пользоваться диаграммами осадок носом и кормой.

Примеры решения типовых задач

 

Задача № 14.1

Определить изменение посадки д/э «Пенжина» после снятия груза массой 280 т при DW = 6540 т, ; ρ =1,01 т/м 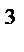; Мд=14000 т/м, если абсцисса центра массы снимаемого груза 5,0 м.

Решение:

По грузовой шкале д/э «Пенжина» по заданному DW определяем среднюю осадку и число тонн на 1 см осадки:

d = 7,54 м, q =18,5 т/см.

Изменение средне осадки: δd = m/ q = 280/18,5 = 15,13 см = 0,1513 м.

По КЭТЧ при известной средней осадке находим Xf = - 0,4 м.

δDf = - m(Х – Xf) /Мд = - 0,092м.

δd н = δd + (0,5L – Xf) δDf/L = - 0,1513 + (0,5· 123 +0,4) (- 0,092/123) =  

 - 0,197м.

 δd к = δd - (0,5L + Xf) δDf/L = - 0,1513 - (0,5· 123 - 0,4) (- 0,092/123) =

 - 0,105 м

 

Задача №14.2

Для т/х « Новгород » выполнить оперативный контроль изменения осадок оконечностей от приема 360 т груза при исходных значениях d н = 8,0 м; d к = 8,5 м, если абсцисса центра масс груза 30 м

Решение:

 d ср = d н + d к/2 = 8 +8,5 / 2 = 8,25 м.

По рис 3.6 находим изменение осадок носом и кормой при приеме 100 тонн груза δd н1 = 0134 м; δd к2 = - 0,036 м
   Рассчитываем изменение осадок от приема 360 тонн груза

δd н = 360*0,134/100 = 0,4824 м

δd к = 360*(-0,036/100) = - 0,1296 м

Задание

На практическом занятии необходимо решить задачи из § 3.3 задачника [3]. Основные зависимость и примеры решения типовых задач в § 3.1-3.2 [3]. Номера задач и их количество определяет преподаватель.

 

Вопросы для самоконтроля

1. Назовите условия равновесия плавающего судна и где на практике их применяют?

2. Почему при посадке судна с большим дифферентом для определения характеристик плавучести судна нельзя пользо­ваться кривыми элементов теоретического чертежа?

3. Почему ордината центра величины судна, плавающего без крена, равна нулю?

4. Как влияет увеличение осадки судна на величину числа тонн на 1 см осадки?

5. Почему при приеме малого груза для определения осадки пользуются числом тонн на 1 см осадки, а не грузовым разме­ром или грузовой шкалой?

6. Чем объяснить, что летом осадка судна допускается боль­ше, чем зимой.

Литература: [1] стр.50-68,

………………[3] стр.27-42,

                               [4] стр. 43-55.

 

 

ПрактическОЕ ЗАНЯТИЕ №15

Решение практических задач по темам:

Определение влияние приема или снятия малого груза на остойчивость и посадку судна; Влияние подвешенного и жидкого грузов на остойчивость судна

Теоретическая часть

Целью данной работы является получение обучающимися общих сведений об остойчивости судов и методике ее контроля в процессе эксплуатации судов. Помимо этого, курсанты (сту­денты) должны научиться рассчитывать посадку судна при перемещении или приеме грузов на судно.

Знакомясь с темой, необходимо повторить определение ста­тических моментов и моментов инерции плоских фигур, дифференцирование функций, определение центра тяжести системы тел, когда одно из них перемещается в каком-либо направле­нии, и вращение тела вокруг оси.

Остойчивостью называется способность судна противодействовать силам, отклоняющим его от положения равновесия, и возвращаться в первоначальное положение равновесия после прекращения действия этих сил. Остойчивость судна меняется с увеличением угла наклонения и при некотором его значении полностью утрачивается. Принято различать остойчивость судна при малых углах наклонения (начальную остойчивость) и остойчивость на больших углах наклонения. В зависимости от направлений наклонения судна изучают поперечную остойчивость и продольную остойчивость.

Если наклонение судна происходит без значительных угловых ускорений (перекачивание жидких грузов, медленное поступление воды в отсек), то остойчивость называют статической.

В ряде случаев наклоняющие судно силы действуют внезапно, вызывая значительные угловые ускорения (шквал ветра, накат волны и т.п.). В таких случаях рассматривают динамическую остойчивость.

Курсанту большое внимание следует обратить на критерии остойчивости: метацентрические высоты и плечо статической остойчивости; твердо усвоить, что метацентрические формулы справедливы только для бесконечно малых углов на­клонения, когда кривую центров величины можно заменить дугой окружности.

Перед выводом формул для определения метацентрических радиусов следует изучить теорему Эйлера, которая объясняет, почему ось наклонения при дифференте не совпадает с ми­делем.

Примеры решения типовых задач

 

Задача 15.1

 

Как измениться поперечная МВ судна после перемещения во время ремонта главного двигателя массой 15 т. из машинного отделения, где аппликата его ЦМ 1,5 м, и установки его на палубу, когда аппликата ЦМ двигателя z₁ = 4,4 м. Δ = 355 т.

Решение:

δh = - m ( z1 - z) / Δ = -15(4,4 – 1,5)/355 = - 0,12м

 

Задача № 15.2

 

Как изменится МВ д/э «Пенжина», если для обеспечения прочности перекачать балласт из цистерн №4 ( Р = 86 т; z = 1,11 м), № 7( Р = 222 т; z = 4,47м) и № 5 ( Р = 64т; z = 0,64м) в цистерны № 14 ( Р = 336т; z = 8,67 м) и № 13( Р = 36 т; z = 1,76 м) ? Цистерны запрессованы. Δ = 9400т.

 

Решение:

При данном перекачивании балласта изменяется его центр тяжести относительно основной плоскости. Определим z1 и z2 – аппликаты ц.т балласта до и после перекачки в цистерны.

 z1 =  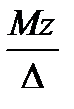=  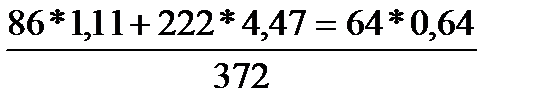= 3,03 м

 z2=  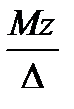=  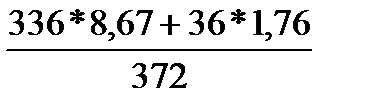= 8 м

Изменение МВ :

δh = - m ( z2 - z1) / Δ = - 372(8 - 3,03)/9400 = - 0,196 м

 

Задача № 15.3

 

Как изменится поперечная МВ судна массой 14000 т с начальной МВ h = 0,75 м и осадкой 7,0 м после заполнения прямоугольного в плане танка двойного дна на половину его высоты топливом с ρ = 0,89 т/м³. Длина танка 19 м, высота двойного дна 1,1 м, число тонн на 1 см осадки 22 т/с; ширина В = 8 м.

Решение:

Определим объем топлива в танке:

v = l·b·H/2 = 19·8·1,1/2 = 83,6 м³

Масса топлива m = ρ · v = 0,89· 83,6 = 74,4 т

Изменение МВ судна определяем по формуле:

δh = 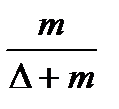(d + 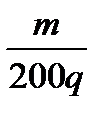 - h – z - ix /v )

δh = 74,4(7,0 + 74,4/200·22 – 0,75 – 0,275 –810,66/83,6)/(14000 + 83,6)

ix = l·b³/12 = 810,66 м⁴

δh = - 0,01957 м.

Задание

На практическом занятии необходимо решить задачи из § 4.6 задачника [3]. Основные зависимость и примеры решения типовых задач в § 4.1,4.5 [3]. Номера задач и их количество определяет преподаватель.

Вопросы для самоконтроля

1. Где при выводе формулы метацентрического радиуса ис­пользуется теорема Эйлера?

2. Какое допущение принимается при выводе формулы пле­ча статической остойчивости для бесконечно малых углов наклонения?

3. Когда следует учитывать влияние дифферента на попе­речную остойчивость судов?

4. Как от диаграммы статической остойчивости перейти к кривой восстанавливающего момента?

5. Бывают ли суда, у которых остойчивость при приеме Малого груза на днище падала бы?

7. Почему при приеме большого груза нельзя для расчетапосадки и остойчивости судна пользоваться формулами, вы­ веденными для приема малого груза?

 

Литература: [1] стр.69-99,

………………[3] стр.43-68,

                               [4] стр. 56-77.

ПрактическОЕ ЗАНЯТИЕ №16