Термин «вейвлет» (wavelet) дословно переводится как «маленькая волна» или «всплеск». За последние десятилетия функции с графиком типа всплеска стали все чаще применяться для разложения радиотехнических сигналов вместо гармонических волн. Теория вейвлетов является мощным дополнением Фурье-анализу и обеспечивает более гибкую технику обработки сигналов. По сравнению с разложением сигналов на ряды Фурье вейвлеты способны с гораздо более высокой точностью представлять локальные особенности сигналов, вплоть до разрывов 1-го рода (скачков). В отличие от преобразований Фурье, вейвлет–преобразование одномерных сигналов обеспечивает двумерную развертку, при этом частота и координата рассматриваются как независимые переменные, что дает возможность анализа сигналов сразу в двух пространствах. Особенно важна принципиальная возможность вейвлетов представлять модулированные сигналы, являющиеся адекватными моделями процессов, происходящих в каналах связи и устройствах их обработки.
Вейвлеты–это обобщенное название семейств математических функций определенной формы, которые локальны в овремени и по частоте, и в которых все функции получаются из одной базовой (порождающей) посредством ее сдвигов и растяжений по оси времени.
Вейвлет - преобразование радиотехнических сигналов –это представление сигнала в ортонормированном базисе, где в качестве базисных функций выбрано одно из семейств вейвлетов.
Рассмотрим пример N = 22 = 4. Исходную 4-точечную последовательность отсчетов цифрового сигнала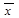 
представим в виде вектора –столбца:
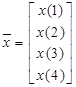(51)
Первый этап преобразования –вычисление двух полусумм и двух полуразностей.
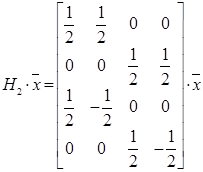(52)
Верхние две строки полученной матрицы усредняют два соседних отсчета сигнала, а нижние –детализируют. Нормируем матрицу для ортогональной системы функций, для этого умножаем все компоненты на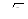 
(матрица Н2). Сохраняем полуразности и преобразуем полусуммы. Этой процедуре соответствует матрица Н1.
, 
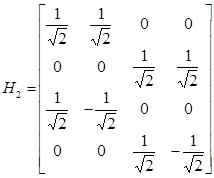(53)
Таким образом, первая строка матрицы H1 усредняет отсчеты, вторая –детализирует, третья и четвертая, образуя единичную матрицу, сохраняют предыдущие полуразности.
Произведение матриц H1 и H2 дает искомое дискретное вейвлет–преобразование вектора :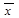
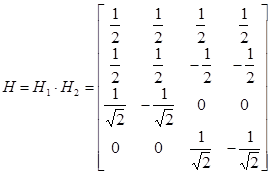(54)
Матрица H является ортогональной и представляет собой известное преобразование Хаара, которое является вейвлет–преобразованием:
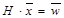, (55)
где элементы вектора-столбца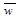 
–вейвлет–коэффициенты.
На практике используется обратное вейвлет-преобразование, т.е. по вектору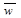 
можно восстановить N-точечную последовательность исходного сигнала . Для этого нужно умножить обе части равенства вейвлет-преобразования на обратную матрицу H-1:
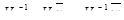
Т.к. произведение H-1H образует единичную матрицу, то
(56)
Следствием ортогональности матрицы H является простота ее обращения, а именно, обычное транспонирование. Поэтому выражение (55) для обратного вейвлет - преобразования примет вид:
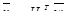(57)
Если каждую строку преобразования Хаара представить в виде ступенчатой функции на единичном интервале, эти функции будут иметь вид, представленный на рис. 69.
| Рис. 69. Вейвлет-функции Хаара |
Ортогональность этих функций следует из принципа их построения и может быть проверена непосредственно.
В качестве примера докажем ортогональность функций (H0 ,Н1):
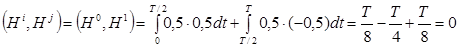
Обобщим матричный алгоритм усреднения и детализации на произвольную N-точечную последовательность, когда N=2v, при этапном процессе преобразования.
На первом шаге ортогональная матрица имеет вид:
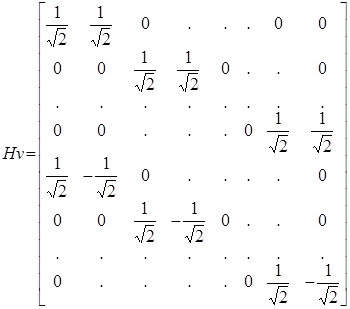(58)
Матрица–квадратная порядкаN=2v. Две матрицы, входящие в состав Hv:
, 
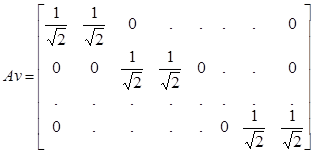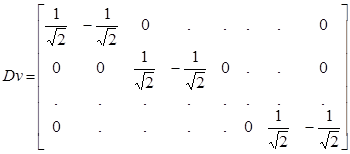, (59)
где подматрицы: Av– преобразование усреднения, Dv–преобразование детализации.
Векторы –столбцы результатов поэтапного вейвлет–преобразования, которые являются векторами коэффициентов усреднения и детализации, имеют вид:
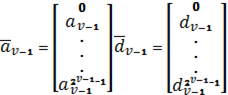(60)
На каждом шаге вейвлет–преобразования сохраняются детализирующие коэффициенты d и обрабатываются результаты усреднения a. Таким образом, итоговый результат вейвлет–преобразования можно представить в виде вектора-столбца, содержащего N=2vэлементов:
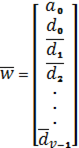(61)
Каждый отсчет дискретного сигнала является вещественным либо комплексным числом. Финитный дискретный сигнал содержит конечный набор таких чисел. В математике существует ряд способов компактного описания совокупности однородных элементов. Одним из них, находящим широкое применение в цифровой обработке, является матричное представление. Приведем основные сведения из теории матриц и проиллюстрируем возможности этой теории при описании дискретных сигналов и их линейных преобразований.
Прямоугольной матрицей А размера m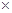 
n или m 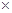n матрицей называется таблица чисел, над которыми выполнимы и однозначны операции сложения, вычитания, умножения и деления на ненулевое число:
A =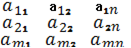 
(62)
Вейвлет Хаа́ра—один из первых и наиболее простых вейвлетов. Он был предложен венгерским математиком Альфредом Хааром в 1909 году. Вейвлеты Хаара ортогональны, обладают компактным носителем, хорошо локализованы в пространстве, но не являются гладкими.
Вейвлет -анализ является разновидностью спектрального анализа, в котором роль простых колебаний играют функции особого рода, называемые вейвлетами. Базисная функция вейвлет–это некоторое "короткое" колебание, но не только.
Понятие частоты спектрального анализа здесь заменено масштабом, и, чтобы перекрыть "короткими волнами" всю временную ось, введен сдвиг функций во времени.
Базис вейвлетов –это функции типа ((t-b)/a), где b - сдвиг, а–масштаб. Функция (t) должна иметь нулевую площадь и, еще лучше, равными нулю первый, 2, 3 и прочие моменты. Фурье-преобразование таких функций равно нулю при t=0 и имеет вид полосового фильтра. При различных значениях масштабного параметра 'a' это будет набор полосовых фильтров.
Задания на практическую работу (Технология выполнения)
Задание 1 Доказать возможность использования вейвлетов Хаара в качестве ортонормированного базиса для разложения радиосигналов наравне с нормированным базисом ортогональных функций Фурье с кратными частотами, предварительно изучив матричное представление функций Хаара.
Пример выполнения задания приведен в теоретической части для Функций H0 ,Н1 .
Доказать ортогональность функций Хаара в соответствии с вариантом (последняя цифра в номере зачетки):
четная (H0 ,Н2), (H0 ,Н3), (H1 ,Н2);
нечетная (H0 ,Н2), (H1 ,Н3), (H2 ,Н3).
Задание 2. Исследовать прямое вейвлет - преобразование гармонического сигнала S ( t )= N * Sin (2 p * N * t ), заданного четырьмя отсчетами на интервале периодичности. X= (N,0,-N,0).
Где N- последняя цифра в номере зачётки студента.
Пример выполнения задания.
Пусть сигнал 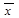= 1*Sin(2p*1*t) задан 4 отсчетами на интервале своей периодичности: [0,1,0,-1]. Тогда вейвлет–коэффициенты 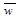дискретного разложения Хаара входного сигнала :
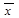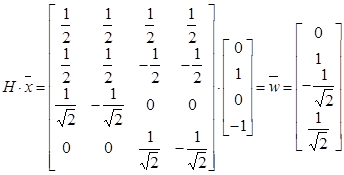
Задание 3. Исследование обратного вейвлет - преобразования сигналов. Определить исходный сигнал по обратному вейвлет - преобразованию, рассчитанному в задании 2.
Пример восстановления сигнала.
Восстановим исходный сигнал 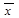по вейвлет– коэффициентам:
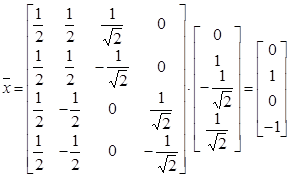
Таким образом, сигнал восстановлен.
5 Контрольные вопросы
1. Что такое математическое представление радиотехнических сигналов?
2. Определение вейвлет-преобразования сигналов.
3. Укажите виды вейвлет-преобразований.
4. На чем основан принцип прямого и обратного вейвлет-преобразований?
Список рекомендуемой литературы
1. Микушин А.В., Сажнев А.М., Седина В.И. «Цифровые устройства и микропроцессоры», СПб.: БХВ-Петербург – 2010.
2. Угрюмов Е.П. «Цифровая схемотехника»,2-е издание. Учебное пособие для ВУЗов. СПб. 2007.
3. Солонина А. И., Улахович Д. А., Арбузов С. М., Соловьева Е. Б., Гук И. И. Основы цифровой обработки сигналов: Курс лекций. СПб.: БХВ-Петербург, 2010.
Министерство образования Нижегородской области
Государственное бюджетное профессиональное образовательное учреждение
«Нижегородский радиотехнический колледж»
ОТЧЁТЫ
по ____________________________ работе
по дисциплине/междисциплинарному курсу/
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
________________________________________________________________________________
| Выполнил (а) студент (ка) группы _______________ ________________________________ Ф.И.О. | Проверил преподаватель _________________________________ Ф.И.О. |
Нижний Новгород
2016 г.
Результаты выполнения работ
| № занятия | Дата выдачи задания | Дата сдачи отчёта | Отметка | Подпись преподавателя |
| №1 | ||||
| №2 | ||||
| №3 | ||||
| №4 | ||||
| №5 | ||||
| №6 | ||||
| №7 | ||||
| №8 | ||||
| №9 | ||||
| №10 | ||||
| №11 | ||||
| №12 | ||||
| №13 | ||||
| №14 | ||||
| №15 | ||||
| №16 | ||||
| №17 | ||||
| №18 | ||||
| №19 | ||||
| №20 | ||||
| №21 | ||||
| №22 | ||||
| №23 | ||||
| №24 | ||||
| №25 | ||||
| №26 | ||||
| №27 | ||||
| №28 | ||||
| №29 | ||||
| №30 |
ОТЧЁТ СТУДЕНТА ПО ВЫПОЛНЕНИЮ
ЛАБОРАТОРНОЙ/ ПРАКТИЧЕСКОЙ РАБОТЫ
1 Тема _________________
2 Цель ___________________
3 Оборудование __________________
4 Ход работы (порядок выполнения) ____________________________
5 Ответы на контрольные вопросы ______________
6 Схемы, таблицы _____________________________________
7 Выводы по работе, обобщения, достигнута ли цель ______________________
Дата: 2018-11-18, просмотров: 392.
