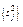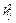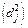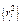Предполагает разбиение на кластеры путем последовательного введения ряда ограничений. При этом вводится так называемая матрица издержек, а задача целочисленного программирования сводится к минимизации общей суммы издержек.
11.2.4. Методы кластеризации
Наиболее популярными являются методы минимальной дисперсии, которые основаны на минимизации внутригрупповых сумм квадратов отклонений.
Метод полных связей (Соренсен) основан на том, что два объекта, принадлежащих одной и той же группе (кластеру), имеют коэффициент сходства, который меньше некоторого порогового значения r. В данном случае r определяет максимально допустимый диаметр подмножества, образующего кластер.
Метод максимального локального расстояния (Мак Нотон-Смит): объекты группируются последовательно по следующему правилу - два кластера объединяются, если максимальное расстояние между точками одного и другого минимально.
Метод Уорда направлен на объединение близко расположенных кластеров, причем в качестве критерия используется сумма квадратов расстояний между каждой точкой (объектом) и средней по кластеру, содержащему этот объект.
Центроидный метод (Сокал и Миченер) основан на определении расстояния между средними значениями кластеров.
Двухгрупповой метод (Сокал и Миченер) опирается на связь между объектом i и кластером I. Эта связь выражается в виде среднего коэффициента сходства между объектом i и всеми объектами, входящими в кластер I.
Метод групповых средних (Ланс, Уильямс) определяет среднее сходство между двумя кластерами I и J как среднее сходство между всеми парами объектов из I и J.
Большинство из упомянутых методов предполагает последовательную процедуру кластеризации. Некоторые разногласия между авторами касаются начального этапа кластеризации. Так, Боннер предлагает метод, в котором начальная точка выбирается случайно, и все объекты, лежащие на расстоянии d £ r от начальной точки, принимаются за первый кластер. Из оставшихся точек снова случайным образом выбирается объект, и процесс повторяется до тех пор, пока все точки не будут принадлежать к определенным кластерам.
Хиверинен выбирает в качестве начального объекта кластеризации не случайную, а «типическую» точку, причем все эти точки лежат на минимальном расстоянии от центра оставшегося множества объектов.
В процедуре Болла и Холла первоначальные К кластеров формируются случайным отбором k точек, к которым затем присоединяется каждая из оставшихся n – k точек (по минимальному расстоянию к той или иной из них).
Другие методы (Мак Квин, Себестьен, Дженсен, Форджи и др.) можно рассматривать как модификации вышеизложенных методов кластеризации.
11.2.5. Представление данных
Данные кластеризации можно наглядно представить в двумерном пространстве в виде дендрограмм или разветвленного (древовидного) графа. В том и другом случае в качестве исходных данных служат матрица сходства или расстояния между обектами.
Рассмотрим в качестве примера корреляционную матрицу (матрицу сходства) следующего вида (табл. 11.2):
Таблица 11.2
| Объекты (признаки) | A | B | C | D | E | F |
| A | 1,00 | 0,35 | 0,92 | 0,50 | 0,42 | 0,72 |
| B | 1,00 | 0,47 | 0,67 | 0,65 | 0,54 | |
| C | 1,00 | 0,38 | 0,24 | 0,78 | ||
| D | 1,00 | 0,84 | 0,44 | |||
| E | 1,00 | 0,35 | ||||
| F | 1,00 |
Каждая из шести переменных, фигурирующих в матрице, обозначена латинскими буквами от A до F. Заполнена только половина матрицы, поскольку верхняя правая и нижняя левая половины зеркально отражают друг друга (rAB = rBA, rBF = rFB и т.д.). По главной диагонали матрицы коэффициенты корреляции соответствуют единицам (rxx = 1).
Объединение переменных в кластеры производится, начиная с максимального коэффициента корреляции. При этом для построения дендрограммы переменные связываются между собой на данном уровне коэффициента корреляции r или меры расстояния d = 1 – r2. Для облегчения работы эти значения округляются до 1-го знака после запятой. Так, максимальный коэффициент корреляции – между переменными A и C (r = 0,92), следовательно, переменные связываются между собой на уровне ~ 0,9. Следующий за первым (по мере убывания) коэффициент корреляции между переменными D и E равен 0,84 (переменные связываются друг с другом на уровне ~ 0,8). Третий по убыванию коэффициент между переменными C и F соответствует 0,78; следовательно, на уровне ~ 0,8 мы можем «привязать» к переменным A и C (а они уже связаны друг с другом) еще и переменную F и т.д. Таким образом, мы последовательно связываем друг с другом все переменные, формируя дендрограмму (аналогично построению «родословного дерева» исследуемых признаков в биологии).
Результирующая дендрограмма, построенная на основании корреляционной матрицы между шестью переменными, представлена на рисунке. Чисто визуально по внешнему виду дендрограммы трудно сделать однозначный вывод о том, сколько же кластеров она включает (два, три или четыре). Иногда число кластеров задается самим экспериментатором. Однако чаще всего заключение о числе результирующих кластеров можно сделать по величине критического коэффициента корреляции. Считается, что переменные объединены в один кластер, если уровень связи между ними выше критического.r
1,0_ F A C D E B
|
0,9
0,8
0,7
0,6
0,5
0,4 |
|
|
|
|
|
| ||||||
|
|
|
|
| |||||||||
|
|
|
|
|
|
|
| ||||||
|
|
|
|
| |||||||||
|
|
| |||||||||||
Рис. 11.1. Дендрограмма признаков, построенная на основе матрицы корреляций.
Представление данных в виде разветвленного графа несколько более произвольно, хотя и здесь относительные расстояния между переменными соответствуют степени связи или различий между ними.

Рис. 11.2. Древовидный (разветвленный) граф:
Как уже отмечалось, по данным кластерного анализа можно составить представление о том, какие психологические признаки фигурируют в одной группе, а какие относятся к разным. Например, если при комплексном психодиагностическом обследовании одновременно определяются характеристики эмоциональной, интеллектуальной и мотивационной сферы испытуемых, то следует ожидать, что характеристики одной и той же сферы объединятся в один кластер, а относящиеся к разным сферам попадут в разные кластеры.
Для кластерного анализа существуют специальные пакеты компьютерных программ, значительно облегчающих работу исследователей в этом направлении.
Факторный анализ
Факторный анализ является одним из наиболее мощных способов анализа данных в многомерной статистике. Впервые (в начале ХХ столетия) он был использован именно для анализа результатов психологических исследований.
В данной главе не ставится цель детального изложения всевозможных методов, вариантов и модификаций факторного анализа. Использование современной компьютерной техники и готовых пакетов программ избавляет исследователя от необходимости заниматься рутинной вычислительной работой. Наша задача состоит в том, чтобы дать психологу общие представления о возможностях факторного анализа, об основных теоретических положениях, лежащих в его основе, а также интерпретации данных, получаемых в результате факторного анализа.
11.3.1. Основные принципы факторного анализа
Факторный анализ представляет собой набор моделей и методов, предназначенных для «сжатия» слишком больших массивов информации. В качестве исходного материала для факторного анализа служат матрицы корреляций между различными признаками (параметрами) исследуемых объектов. Если таких признаков достаточно много, матрица становится весьма громоздкой и работа с нею представляет большие трудности.
В основе факторного анализа лежит следующая гипотеза. Наблюдаемые или измеряемые параметры являются лишь косвенными характеристиками изучаемых объектов, так сказать, их внешними проявлениями. На самом же деле существуют внутренние (скрытые, не наблюдаемые непосредственно) характеристики, число которых невелико и которые определяют значения наблюдаемых параметров. Эти внутренние характеристики называют факторами. Отдельные же наблюдаемые значения переменных являются линейными комбинациями факторов, которые не могут быть обнаружены в процессе наблюдения, но могут быть вычислены.
Задача факторного анализа состоит в том, чтобы представить наблюдаемые параметры в виде линейных комбинаций факторов и, возможно, некоторых дополнительных величин, связанных в первую очередь с ошибками измерения. Несмотря на то, что сами факторы изначально не определены, такое разложение может быть получено и, более того, значения каждого из факторов могут быть вычислены непосредственно в ходе анализа.
Задача вычисления факторов может быть интерпретирована так, что исследуемые параметры объединяются в группы, причем параметры, входящие в одну группу, связаны между собой сильной корреляционной связью, а входящие в разные группы – слабо коррелируют друг с другом.
Конечным результатом факторного анализа является получение содержательно интерпретируемых факторов, воспроизводящих матрицу коэффициентов корреляции между переменными.
Применение факторного анализа в различных областях психологических наук, показало, что определяемые факторы, как правило, хорошо интерпретируются как некоторые существенные внутренние характеристики изучаемых признаков (психологических особенностей субъектов).
В качестве начального этапа факторного анализа, так же как и других статистических методов, используется определение дисперсии каждого параметра xj (j = 1, 2, ..., n) по определенному числу повторностей i (i = 1, 2, ..., N), а также попарное вычисление корреляции между всеми изучаемыми параметрами.
В модели классического факторного анализа требуется наилучшим образом аппроксимировать корреляции, причем основная модель анализа может быть записана в следующем виде:
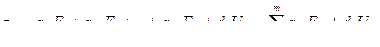 (11.7)
(11.7)
(i = 1, 2, ..., N; j = 1, 2, ..., n).
В этом выражении zj – общая нормированная дисперсия, F1, F2, ..., Fm – общие факторы (как правило m < n), Uj – характерный фактор, который учитывает «остаточную» (связанную с различными погрешностями) дисперсию; a1, a2, ..., am, которые являются коэффициентами при факторах, называют нагрузками. Другими словами, факторная нагрузка есть не что иное как коэффициент корреляции между фактором и исследуемой переменной.
Классификация факторов:
Фактор называется генеральным, если все его нагрузки значительно отличаются от нуля, т.е. он имеет нагрузки от всех переменных.
Фактор называется общим, если хотя бы две его нагрузки значительно отличаются от нуля (т.е. он имеет нагрузки от двух и более переменных). Число высоких нагрузок переменной на общие факторы называется ее сложностью.
Одной из особенностей факторного анализа является понятие компонентов дисперсии.
Общность параметра zj, связанная с общими факторами, представляет собой часть единичной дисперсии переменной, которую можно приписать общим факторам. Она равна квадрату коэффициента множественной корреляции между переменной и общими факторами, т.е. сумме квадратов факторных нагрузок:
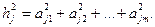 (11.8)
(11.8)
(j = 1, 2, ..., n). По сути дела, общности представляют собой диагональные элементы матрицы корреляций между исследуемыми переменными.
Характерность представляет собой часть единичной дисперсии переменной, которая не связана с общими факторами, т. е. вклад характерного фактора Uji. Характерность показывает, насколько в общих факторах учтена суммарная дисперсия параметра. Характерность можно разбить на две составляющие – специфичность и дисперсию, обусловленную ошибкой.
Специфичность – доля характерности, которая тем или иным образом связана с действительной спецификой изучаемого параметра.
Дисперсия ошибки (ненадежность) параметра связана с несовершенством измерений.
Надежность есть разница между полной дисперсией и дисперсией ошибки, т.е. представляет собой сумму общности и специфичности. Значение надежности является верхней границей общности. Разница между надежностью и общностью является мерой специфической дисперсии, присущей только одной определенной переменной. Переменные, характеризующиеся малой надежностью, в факторный анализ включаться не должны.
В математическом выражении компоненты дисперсии выглядят следующим образом:
1) полная дисперсия: rj2 = hj2 + bj2 + ej2 = hj2 + dj2 = 1. (11.9)
2) надежность: 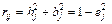 (11.10)
(11.10)
3) общность: 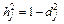 (11.11)
(11.11)
4) характерность: 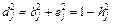 (11.12)
(11.12)
5) специфичность: 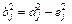 (11.13)
(11.13)
6) дисперсия ошибки: ej = 1 = 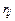 . (11.14)
. (11.14)
Более наглядно соотношения компонентов дисперсии можно представить в виде следующей схемы (табл. 11.3):
Таблица 11.3
| Полная дисперсия | ||||||
| Общность | Характерность | |||||
|
| Специфичность | Дисперсия | ||||
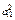
| 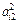
| 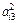
| ... 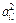 ... ...
| 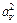
| 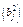
| ошибки 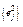
|
|
| Дисперсия | |||||
| Надежность | ошибки 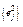
| |||||
Некоторые исследователи не вводят предположения о существовании специфических факторов и даже факторов ошибки. При этом число общих факторов m может быть меньше или равным числу параметров n.
Кроме алгебраического представления факторной модели, иногда используются геометрические представления о корреляциях между изучаемыми параметрами как множестве векторов в многомерном пространстве. При этом задача факторного анализа состоит в попарном измерении расстояний между векторами и выявлении областей «сгущения» векторов, соответствующих отдельным факторам.
11.3.2. Основные методы, используемые в факторном анализе
Метод главных компонент (компонентный анализ)
Каждый из N объектов представляется в виде точки в n-мерном пространстве, каждая ось которого соответствует одному из параметров. Облако точек имеет форму, близкую к m-мерному эллипсоиду, и становится идеальным эллипсоидом в случае нормального распределения. Оси эллипсоида соответствуют главным компонентам. Следовательно, в компонентном анализе производится вращение исходной системы координат к новой системе в полном пространстве параметров – ортогональное преобразование, при котором каждый из n параметров выражается через n главных компонент. Целью вращения является нахождение в пространстве общих факторов одной из возможных осей координат, которая должна быть наложена на конфигурацию векторов для получения факторной структуры. Важным свойством компонент является то, что каждая из них по порядку учитывает максимум суммарной дисперсии параметров. Другими словами, первая главная компонента есть линейная комбинация исходных параметров, учитывающая максимум их суммарной дисперсии; вторая главная компонента не коррелирует с первой и учитывает максимум оставшейся дисперсии и т.д. до тех пор, пока вся дисперсия не будет учтена. Сумма дисперсий всех главных компонент равна сумме дисперсий всех исходных параметров. При этом принято выражать параметры в стандартной форме, при которой дисперсия параметра равна единице (следовательно, суммарная дисперсия равна n).
Метод главных факторов
Представляет собой приложение метода главных компонент к редуцированной корреляционной матрице, у которой на главной диагонали стоят значения общностей. Выражение для определения коэффициентов при общих факторах записывается уравнением zj = aj1F1 + ... + ajpFp + ... + ajmFm (j = 1, 2, ..., n), в котором не учитывается специфический фактор.
Сумма квадратов факторных коэффициентов дает значение общности данного параметра, а член 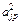 указывает на вклад фактора Fp в общность параметра zj.
указывает на вклад фактора Fp в общность параметра zj.
На первой стадии анализа ищут коэффициенты при первом факторе так, чтобы сумма вкладов фактора в суммарную общность была максимальной. Эта сумма равна V1 = 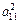 +
+ 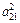 + ... +
+ ... + 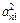 .
.
Для определения коэффициентов при втором факторе F2 необходимо максимизировать функцию V2 = 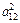 +
+ 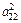 + ... +
+ ... + 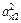 , которая представляет собой сумму вкладов F2 в остаточную общность и т.д.
, которая представляет собой сумму вкладов F2 в остаточную общность и т.д.
В отличие от метода главных компонент, на главной диагонали стоят числа, меньшие единицы (оценки общностей), поэтому m < n. Процедура факторизации в данном случае несколько проще, нежели при использовании метода главных компонент, и процесс прекращается, когда сумма собственных значений становится равной суммарной общности n параметров.
Центроидный метод
Название метода происходит от понятия центроида, или центра тяжести. Поскольку параметры можно рассматривать как набор n векторов в m-мерном пространстве, где m число общих факторов, то скалярное произведение любой пары векторов соответствует коэффициенту корреляции между соответствующими векторами (напомним, что величина коэффициента корреляции равна косинусу угла между двумя векторами).
Процедура анализа состоит в повороте системы координат таким образом, чтобы первая ось проходила через начало координат и «центр тяжести» n точек концов векторов. После этого можно вычислить проекции векторов (координаты параметров) на первую ось новой системы. С помощью специальных алгоритмов определяются коэффициенты при первом центроидном факторе.
Для нахождения второго фактора вычисляют матрицу первых остатков. Остаточные корреляции вычисляются как скалярные произведения пар остаточных векторов в пространстве m - 1 измерений. Процедура последовательно повторяется до тех пор, пока не будут вычислены факторные веса и нагрузки всех остальных факторов.
В отличие от предыдущих методов, в центроидном методе используется процедура «отражения», когда после вычисления нагрузки каждого фактора все оставшиеся отрицательные векторы поворачивают на 180° (напомним, что уровень связи не зависит от знака корреляции).
Метод минимальных остатков
Имеет ряд модификаций, из которых наиболее эффективным является метод последовательных замен (процедура Гаусса-Зейделя). Он представляет собой процедуру, в которой на каждом шаге производится небольшое изменение значений переменных (параметров) и вместо прежних значений принимаются эти новые значения. Если замены вводятся только в одну строку матрицы, то вычисленные коэффициенты корреляции будут линейными, а целевая функция – квадратичной функцией этих замен. Процесс поочередно повторяется для всех параметров; последовательно получаются приближения строк факторных нагрузок, минимизирующих целевую функцию.
Дата: 2018-11-18, просмотров: 759.