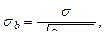Зависимость типа y = a + bx называется линейной. Для математического описания этой формы зависимости достаточно определить величину коэффициента b и свободного члена a в координатах y = f ( x ).
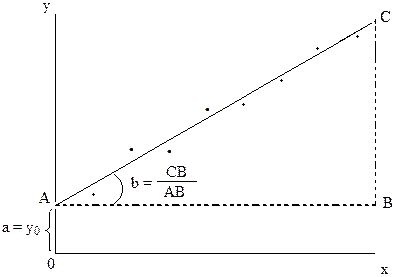
Рис. 9.2. Параметры линейной зависимости (объяснение в тексте)
В данном случае b – тангенс угла наклона функции b > 0, если функция возрастает и b < 0 в случае убывающей функции. Если же функция параллельна оси абсцисс, т.е. значения yi не зависят от аргумента, то b = 0.
a = y0 – ордината точки при x = 0. Величина свободного члена а положительна (a > 0), если точка пересечения функции с осью ординат лежит выше нуля; a < 0, если точка пересечения лежит ниже начала координат.
Метод наименьших квадратов основан на одном из свойств среднего арифметического значения: сумма квадратов отклонений от среднего меньше суммы квадратов отклонений от любой другой точки (см. 4. 3). Таким образом, вычисляя параметры a и b линейной функции, мы задаем такое положение линии, при котором сумма квадратов отклонений (расстояний) эмпирических (экспериментальных) точек от теоретически рассчитанной прямой минимальна.
Вычисление тангенса угла наклона функции ( b )
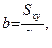где 
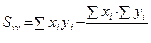и 
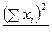. (9.1)
Таким образом,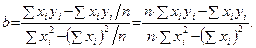 
(9.2)
Другими словами, для вычисления тангенса угла наклона достаточно рассчитать две уже знакомые нам величины – дисперсию значений аргумента ( Sxx ) и ковариацию ( Sxy ).
Вычисление свободного члена (а) в уравнении линейной регрессии:
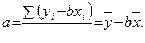(9.3)
Кроме двух вышеуказанных показателей, при использовании метода наименьших квадратов часто вычисляют величину ошибки регрессии (s ). Ошибка регрессии по сути является аналогом стандартного отклонения. Она отражает степень точности определения положения линейной функции в данной системе координат.
Вычисление ошибки регрессии:
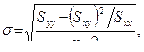где 
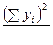. (9.4)
Величина ошибки регрессии может отражать:
а) величину разброса экспериментальных точек относительно теоретических значений функции, т.е. она тем больше, чем больше сумма квадратов отклонений от теоретической функции (при полном совпадении экспериментальных и теоретических значений s = 0);
б) нелинейность функции в данной системе координат (для определения нелинейности функции не следует пренебрегать ее графическим изображением и не следует пытаться описать уравнением линейной регрессии функцию, которая явно не является линейной).
Ошибка коэффициента уравнения линейной регрессии (тангенса угла наклона) определяется по формуле:
|
|
(9.5)
где σ – величина ошибки регрессии, m - число измерений для каждого y (при условии повторения эксперимента).
В тех случаях, когда возникает необходимость сравнить между собой две индивидуальные или усредненные функции на предмет достоверности их различий, можно использовать величины тангенса угла наклона с соответствующим доверительным интервалом: b1 ± t ×sb и b2 ± t ×sb. Вывод о достоверности различий делается в том случае, когда доверительные интервалы для двух испытуемых (или двух выборок) не перекрываются между собой (так же как и в случае определения достоверности различий между выборками по критерию Стьюдента (см. подраздел 7.4.)).
Для того чтобы приобрести определенный навык в расчетах подобного рода, рассмотрим задачу из области психофизики.
Условие задачи
В психофизических исследованиях субъективной оценки громкости (R) тонального звука, проведенных на 50 испытуемых, были получены следующие данные (табл. 9.1):
Таблица 9.1
| I , дБ | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 |
| R | 1,4 | 2,9 | 6,8 | 10,5 | 17,4 | 27,5 | 66,1 | 107,2 | 158,5 |
Задание
Принимая, что усредненные оценки громкости описываются степенной функцией Стивенса, с помощью метода наименьших квадратов рассчитать основные параметры психофизической функции субъективной оценки громкости.
Решение
1. Учитывая тот факт, что степенная функция Стивенса y = k·S n есть в то же время двойная логарифмическая функция типа log y = n·log S + C, и то, что шкала децибелов представляет собой логарифмическую шкалу (20 дБ = 1 лог. ед.), проводим следующие преобразования:
а) преобразуем физическую шкалу сенсорного стимула в логарифмические единицы по десятичному основанию по принципу х = I / 20.
б) логарифмируем значения субъективной шкалы по принципу y = lg R (табл. 9.2).
Таблица 9.2
| x | 0,5 | 1,0 | 1,5 | 2,0 | 2,5 | 3,0 | 3,5 | 4,0 | 4,5 |
| y | 0,15 | 0,46 | 0,83 | 1,02 | 1,24 | 1,44 | 1,82 | 2,03 | 2,20 |
2. Вычисляем предварительные (рабочие) параметры:
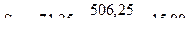
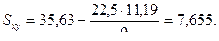
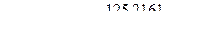
3. Вычисляем основные параметры психофизической функции:
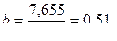
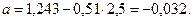
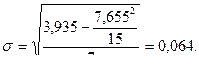
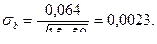
Вывод
Субъективная оценка громкости тонального звука для данной группы испытуемых описывается степенной функцией Стивенса следующего типа:
у = 0,51х – 0,032, или R = 1,076 I0,51 + C (антилогарифм 0,032 равен –1,076).
В некоторых случаях возникает задача сравнения между собой психофизических функций у двух или более испытуемых на предмет достоверности их различий. Попарное сравнение можно сделать, определяя тангенс угла наклона функции с доверительным интервалом. Так, различия можно считать статистически достоверными, если интервалы b1 ± tn-1·σb1 и b2 ± tn-1·σb2 не имеют области перекрытия.
Множественная регрессия
Предположим, что на величину исследуемого признака (y) оказывает влияние большое число разнообразных факторов:
y = a + b1x1 + b2x2 + ... + bmxm. (9.3)
где x1, x2, … xm – факторы, оказывающие влияние на переменную величину. Коэффиценты при факторах по сути представляют собой коэффициенты корреляции факторов с результирующим признаком. Для определения коэффициентов b1, b2, ..., bm (т. е. степени влияния факторов x1, x2, ..., xm на параметры функции), а также свободного члена уравнения а существуют специальные алгоритмы и компьютерные программы. Расчет множественной регрессии на калькуляторе чрезвычайно громоздок, поэтому, как правило, вычисления ведутся на компьютере.
По сути дела задача множественного регрессионного анализа сводится к выявлению тех факторов, которые оказывают наиболее существенное влияние на величину исследуемого признака, и исключению тех факторов, влияние которых незначительно.
Задачи по теме
9.1. Логарифмическая функция типа R = 2,375 lg m – 2,292; s = 0,171; sb = 0,048.
9.2. Психофизические функции: lg R1 = 0,676 lg S – 0,681 и lg R2 = 0,671 lg S – 0,577.
Для 1-го испытуемого: b = 0,676; a = –0,681; s = 0,026; sb = 0,022. Для 2-го испытуемого: b = 0,671; a = –0,577; s = 0,056; sb = 0,048. Поскольку b1 = 0,676 ± 0,052 и b2 = 0,671 ± 0,111, следовательно, различия между психофизическими функциями статистически недостоверны.
Задача 9. 1
Условие задачи
5 испытуемых оценивали субъективную тяжесть предлагаемых им грузов массой от 20 до 1280 г. Использовался метод категориального шкалирования (группировки), причем тяжесть каждого груза предлагалось оценить одной из пяти категорий: 1 – очень легкий, 2 – легкий груз, 3 – груз средней тяжести, 4 – тяжелый и 5 – очень тяжелый. Получены следующие результаты:
| Испытуемый | Масса груза в граммах | ||||||
| 20 | 40 | 80 | 160 | 320 | 640 | 1280 | |
| 1 2 3 4 5 | 1 1 1 1 1 | 1 2 1 1 2 | 2 2 2 2 2 | 3 3 2 3 4 | 3 4 3 4 4 | 4 5 4 5 5 | 5 5 5 5 5 |
Задание
По данным, усредненным по 5 испытуемых, построить психофизическую функцию категориальной оценки. Определить форму зависимости и рассчитать основные параметры функции.
Задача 9. 2
Условие задачи
Двое испытуемых визуально оценивали площадь круга в относительных единицах. Получены следующие данные:
| Площадь круга, см2 | S | 10 | 14 | 20 | 28 | 40 | 56 | 79 | 112 | 158 |
| Оценки 1-го испытуемого | R1 | 1,0 | 1,2 | 1,5 | 2 | 2,5 | 3,6 | 4 | 5 | 6 |
| Оценки 2-го испытуемого | R2 | 1 | 1,5 | 2 | 2,5 | 3 | 4 | 5 | 6 | 8 |
Задание
1. Методом подбора координат определить форму психофизической функции для обоих испытуемых (использовать полулогарифмические и двойные логарифмические координаты).
2. Методом наименьших квадратов рассчитать основные параметры психофизических функций (b , a , s и sb) для обоих испытуемых.
3. Используя величины b1 и b2, определить достоверность различий между психофизическими функциями двух испытуемых (для 1-го уровня значимости tст. = 2,31).
З а д а ч а 9. 3
Условие задачи
Шкалирование яркости светового сигнала, проведенное 50 испытуемыми, обнаружило следующие соотношения между физической яркостью (B) и ее субъективной оценкой (RB):
| B, кд/м2 | 1 | 2,5 | 10 | 25 | 100 |
| Rв | 1,0 | 1,5 | 2,2 | 3,2 | 4,7 |
| B, кд/м2 | 250 | 1000 | 2500 | 10000 | 25000 |
| Rв | 6,8 | 10,1 | 14,8 | 21,7 | 32,0 |
Задание
Принимая, что субъективная оценка яркости описывается степенной функцией Стивенса, построить психофизическую функцию в координатах lg R = f (lg B) и определить ее основные параметры (b , a , s и sb).
З а д а ч а 9. 4
Условие задачи
10 испытуемых оценивали длительность тонального звука методом кросс-модального подбора, рисуя линии соответствующей длины на экране дисплея. Получены следующие результаты:
| Испытуемый | Длительность звука в секундах | ||||||
| 0,25 | 0,5 | 1,0 | 2,0 | 4,0 | 8,0 | 16,0 | |
| Ю. П. Ю. М. Л. Г. И. Т. Т. З. Е. К. Н. У. М. Х. Л. К. Н. А. | 10 5 10 7 14 6 8 5 6 6 | 16 12 25 15 24 19 19 7 8 10 | 35 29 49 23 44 45 28 9 25 20 | 84 30 50 30 71 54 49 24 80 39 | 82 74 153 58 128 62 112 73 135 43 | 138 152 226 124 241 143 182 190 239 102 | 292 303 267 259 318 193 284 280 310 198 |
Примечание: цифры в таблице соответствуют длине подбираемых линий в миллиметрах.
Задание
1. Методом подбора координат определить форму психофизической функции L = f (T) для данных, усредненных по 10 испытуемым.
2. Методом наименьших квадратов вычислить основные параметры психофизической функции для кросс-модального подбора длины линий к длительности звукового сигнала.
РАЗДЕЛ 10.
Меры влияния
Сущность проблемы
В различных областях психологии часто приходится иметь дело с влиянием на исследуемый признак тех или иных факторов. Понятие фактора в данном случае трактуется чрезвычайно широко: по сути, это любое воздействие, которое может изменять величину исследуемого признака. Так, в клинической практике это может быть действие психотропных препаратов или психотерапевтического воздействия. В педагогической психологии в качестве факторов могут выступать те или иные учебно-воспитательные методики. При исследовании какого-либо психологического признака в разных возрастных группах в качестве фактора может рассматриваться возраст испытуемых и т. д. При влиянии определенных факторов или их совокупности величина исследуемого признака может меняться в ту или иную сторону. Задача состоит в том, чтобы на основании изменения исследуемого признака определить статистическую достоверность (значимость) влияния данного фактора. Для анализа достоверности влияния того или иного фактора, а также для сравнения между собой силы влияния разных факторов используются как параметрические (дисперсионный анализ), так и непараметрические меры влияния (критерий знаков, критерий Т Вилкоксона и др.).
Дата: 2018-11-18, просмотров: 532.
