(тау Кендалла, t)
Коэффициент корреляции Кендалла используется в случае, когда переменные представлены двумя порядковыми шкалами при условии, что связанные ранги отсутствуют. Вычисление коэффициента Кендалла связано с подсчетом числа совпадений и инверсий. Рассмотрим эту процедуру на примере предыдущей задачи.
Алгоритм решения задачи следующий:
1. Переоформляем данные табл. 8.5 таким образом, чтобы один из рядов (в данном случае ряд xi) оказался ранжированным. Другими словами, мы переставляем пары x и y в нужном порядке и вносим данные в столбцы 1 и 2 табл. 8.6.
Таблица 8.6
| xi | yi | Совп. | Инв. |
| 1 2 3 4 5 6 7 8 9 10 11 12 | 3 6 7 1 2 4 9 5 11 8 12 10 | 9 6 5 8 7 6 3 4 1 2 0 0 | 2 4 4 0 0 0 2 0 2 0 1 0 |
| Σ | 51 | 15 |
2. Определяем «степень ранжированности» 2-го ряда (yi). Эта процедура проводится в следующей последовательности:
а) берем первое значение неранжированного ряда «3». Подсчитываем количество рангов ниже данного числа, которые больше сравниваемого значения. Таких значений 9 (числа 6, 7, 4, 9, 5, 11, 8, 12 и 10). Заносим число 9 в столбец «совпадения». Затем подсчитываем количество значений, которые меньше трех. Таких значений 2 (ранги 1 и 2); вносим число 2 в графу «инверсии».
б) отбрасываем число 3 (мы с ним уже поработали) и повторяем процедуру для следующего значения «6»: число совпадений равно 6 (ранги 7, 9, 11, 8, 12 и 10), число инверсий – 4 (ранги 1, 2, 4 и 5). Вносим число 6 в графу «совпадения», а число 4 – в графу «инверсии».
в) аналогичным образом процедура повторяется до конца ряда; при этом следует помнить, что каждое «отработанное» значение исключается из дальнейшего рассмотрения (подсчитываются только ранги, которые лежат ниже данного числа).
Примечание
Для того чтобы не совершать ошибок в подсчетах, следует иметь в виду, что с каждым «шагом» сумма совпадений и инверсий уменьшается на единицу; это понятно, если учесть, что каждый раз одно значение исключается из рассмотрения.
3. Подсчитывается сумма совпадений (Р) и сумма инверсий (Q); данные вносятся в одну и трех взаимозаменяемых формул коэффициента Кендалла (8.10). Проводятся соответствующие вычисления.
 t
t  (8.10)
(8.10)
В нашем случае:
В табл. XIV Приложений находятся критические значения коэффициента для данной выборки: τкр. = 0,45; 0,59. Эмпирически полученное значение сравнивается с табличным.
Вывод
τ = 0,55 > τкр. = 0,45. Корреляция статистически значима для 1-го уровня.
Примечание:
При необходимости (например, при отсутствии таблицы критических значений) статистическая значимость t Кендалла может быть определена по формуле следующего вида:
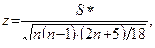 (8.11)
(8.11)
где S* = P – Q + 1, если P < Q, и S* = P – Q – 1, если P > Q.
Значения z для соответствующего уровня значимости соответствуют мере Пирсона и находятся по соответствующим таблицам (в приложение не включены. Для стандартных уровней значимости zкр = 1,96 (для β1 = 0,95) и 2,58 (для β2 = 0,99). Коэффициент корреляции Кендалла является статистически значимым, если z > zкр
В нашем случае S* = P – Q – 1 = 35 и z = 2,40, т. е. первоначальный вывод подтверждается: корреляция между признаками статистически достоверна для 1-го уровня значимости.
Дата: 2018-11-18, просмотров: 735.