Исходный принцип коэффициента корреляции Пирсона – использование произведения моментов (отклонений значения переменной от среднего значения):
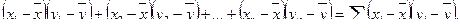 (8.2)
(8.2)
Если сумма произведений моментов велика и положительна, то х и у связаны прямой зависимостью; если сумма велика и отрицательна, то х и у сильно связаны обратной зависимостью; наконец, в случае отсутствия связи между x и у сумма произведений моментов близка к нулю.
Для того чтобы статистика не зависела от объема выборки, берется не сумма произведений моментов, а среднее значение. Однако деление производится не на объем выборки, а на число степеней свободы n - 1.
Величина 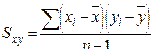 является мерой связи между х и у и называется ковариацией х и у.
является мерой связи между х и у и называется ковариацией х и у.
Во многих задачах естественных и технических наук ковариация является вполне удовлетворительной мерой связи. Ее недостатком является то, что диапазон ее значений не фиксирован, т. е. она может варьировать в неопределенных пределах.
Для того чтобы стандартизировать меру связи, необходимо избавить ковариацию от влияния стандартных отклонений. Для этого надо разделить Sxy на sx и sy:
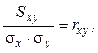 (8.3)
(8.3)
где rxy - коэффициент корреляции, или произведение моментов Пирсона.
Общая формула для вычисления коэффициента корреляции выглядит следующим образом:
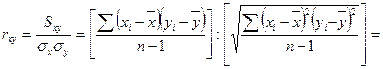
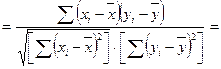 (некоторые преобразования)
(некоторые преобразования)
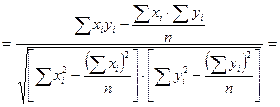
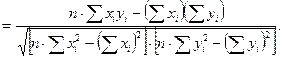 (8.4)
(8.4)
Влияние преобразования данных на rxy:
1. Линейные преобразования x и y типа bx + a и dy + c не изменят величину корреляции между x и y.
2. Линейные преобразования x и y при b < 0, d > 0, а также при b > 0 и d < 0 изменяют знак коэффициента корреляции, не меняя его величины.
Достоверность (или, иначе, статистическая значимость) коэффициента корреляции Пирсона может быть определена разными способами:
По таблицам критических значений коэффициентов корреляции Пирсона и Спирмена (см. Приложение, табл. XIII). Если полученное в расчетах значение rxy превышает критическое (табличное) значение для данной выборки, коэффициент Пирсона считается статистически значимым. Число степеней свободы в данном случае соответствует n – 2, где n – число пар сравниваемых значений (объем выборки).
По таблице XV Приложений, которая озаглавлена «Количество пар значений, необходимое для статистической значимости коэффициента корреляции». В данном случае необходимо ориентироваться на коэффициент корреляции, полученный в вычислениях. Он считается статистически значимым, если объем выборки равен или превышает табличное число пар значений для данного коэффициента.
По коэффициенту Стьюдента, который вычисляется как отношение коэффициента корреляции к его ошибке:
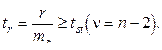 (8.5)
(8.5)
 Ошибка коэффициента корреляции вычисляется по следующей формуле:
Ошибка коэффициента корреляции вычисляется по следующей формуле:
(8.6)
где mr - ошибка коэффициента корреляции, r - коэффициент корреляции; n - число сравниваемых пар.
Рассмотрим порядок вычислений и определение статистической значимости коэффициента корреляции Пирсона на примере решения следующей задачи.
Условие задачи
22 старшеклассника были протестированы по двум тестам: УСК (уровень субъективного контроля) и МкУ (мотивация к успеху). Получены следующие результаты (табл. 8.2):
Таблица 8.2
| №№ | УСК (xi) | МкУ (yi) | №№ | УСК (xi) | МкУ (yi) |
| 1 2 3 4 5 6 7 8 9 10 11 | 27 24 27 30 25 18 28 31 31 30 18 | 18 19 16 13 17 13 19 19 10 24 13 | 12 13 14 15 16 17 18 19 20 21 22 | 24 27 25 37 35 25 22 26 34 25 31 | 12 15 15 23 24 20 14 21 24 17 17 |
Задание
Проверить гипотезу о том, что для людей с высоким уровнем интернальности (балл УСК) характерен высокий уровень мотивации к успеху.
Решение
1. Используем коэффициент корреляции Пирсона в следующей модификации (см. формулу 8.4):
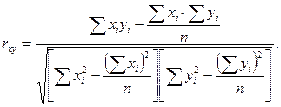
Для удобства обработки данных на микрокалькуляторе (в случае отсутствия необходимой компьютерной программы) рекомендуется оформление промежуточной рабочей таблицы следующего вида (табл. 8.3):
Таблица 8.3
| xi | yi | xi2 | yi2 | xiyi |
| x1 x2 x3 . . . xn | y1 y2 y3 . . . yn | x12 x22 x32 . . . xn2 | y12 y22 y32 . . . yn2 | x1y1 x2y2 x3y3 . . . xnyn |
| Σxi | Σyi | Σxi2 | Σyi2 | Σxiyi |
2. Проводим вычисления и подставляем значения в формулу:
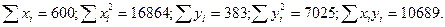
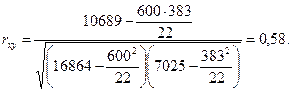
3. Определяем статистическую значимость коэффициента корреляции Пирсона тремя способами:
1-й способ:
В табл. XIII Приложений находим критические значения коэффициента для 1-го и 2-го уровней значимости: r кр. = 0,42; 0,54 (ν = n – 2 = 20).
Делаем вывод о том, rxy > rкр., т. е. корреляция является статистически значимой для обоих уровней.
2-й способ:
Воспользуемся табл. XV, в которой определяем число пар значений (число испытуемых), достаточное для статистической значимости коэффициента корреляции Пирсона, равного 0,58: для 1-го, 2-го и 3-го уровней значимости оно составляет, соответственно, 12, 18 и 28.
Отсюда мы делаем вывод о том, что коэффициент корреляции является значимым для 1-го и 2-го уровня, но «не дотягивает» до 3-го уровня значимости.
3-й способ:
Вычисляем ошибку коэффициента корреляции и коэффициент Стьюдента как отношение коэффициента Пирсона к ошибке:
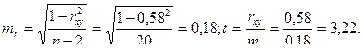
В табл. X находим стандартные значения коэффициента Стьюдента для 1-го, 2-го и 3-го уровней значимости при числе степеней свободы ν = n – 2 = 20: t кр. = 2,09; 2,85; 3,85.
Общий вывод
Корреляция между показателями тестов УСК и МкУ является статистически значимой для 1-го и 2-го уровней значимости.
Примечание:
При интерпретации коэффициента корреляции Пирсона необходимо учитывать следующие моменты:
1. Коэффициент Пирсона может использоваться для различных шкал (шкала отношений, интервальная или порядковая) за исключением дихотомической шкалы.
2. Корреляционная связь далеко не всегда означает связь причинно-следственную. Другими словами, если мы нашли, предположим, положительную корреляцию между ростом и весом у группы испытуемых, то это вовсе не означает, что рост зависит от веса или наоборот (оба этих признака зависят от третьей (внешней) переменной, каковая в данном случае связана с генетическими конституциональными особенностями человека).
3. rxu » 0 может наблюдаться не только при отсутствии связи между x и y, но и в случае сильной нелинейной связи (рис. 8.2 а). В данном случае отрицательная и положительная корреляции уравновешиваются и в результате создается иллюзия отсутствия связи.
4. rxy может быть достаточно мал, если сильная связь между х и у наблюдается в более узком диапазоне значений, чем исследуемый (рис. 8.2 б).
5. Объединение выборок с различными средними значениями может создавать иллюзию достаточно высокой корреляции (рис. 8.2 в).
yi yi yi
| . . . . . . . . . . . | . . . . . . . . . . . | . . . . . + + . . + + + + + |
xi xi xi
а б в
Рис. 8.2. Возможные источники ошибок при интерпретации величины коэффициента корреляции (объяснения в тексте (пункты 3 – 5 примечания))
Дата: 2018-11-18, просмотров: 763.