Однофакторный дисперсионный анализ (ОДА) является достаточно информативным метрическим методом оценки влияния. Используется в тех случаях, когда требуется изучить однократное или повторное действие одного фактора. Говоря о повторном действии фактора, имеется в виду, что фактор представлен несколькими градациями, т. е. имеет 1, 2, 3, ..., J уровней (например, повторный курс лечения психотропным препаратом, повторные сеансы психокоррекции и т. д.).
Для проведения дисперсионного анализа не обязательно проводить измерения на одной и той же выборке, т. е. нет необходимости подвергать одних и тех же субъектов влиянию всех исследуемых градаций фактора. Напротив, для каждого из J уровней (градаций фактора) берется n независимых наблюдений. Естественно, что при таком подходе принимается целый ряд допущений, иногда достаточно произвольных. Предполагается, в частности, что n наблюдений на каждом уровне независимы друг от друга и взяты из нормальной совокупности с дисперсией s2. Предполагается также, что дисперсия s2 одинакова на всех J уровнях (гипотеза однородности, или гомоскедактичности).
Однофакторный дисперсионный анализ включает в себя ряд этапов.
1. Результаты эксперимента представляются в виде следующей таблицы (двумерного массива) (табл. 10.3):
Таблица 10.3
| Условия опыта (градации фактора) | |||||
| 1 | 2 | 3 | ... | J | |
| X11 | x12 | x13 | ... | x1J | |
| Повторные | X21 | x22 | x23 | ... | x2J |
| наблюдения | . | . | . | ... | . |
| . | . | . | ... | . | |
| . | . | . | ... | . | |
| xn1 | xn2 | xn3 | ... | xnJ | |
2. Для каждой выборки испытуемых определяется случайная (внутригрупповая) дисперсия SSW, связанная с вариабельностью переменной внутри каждой градации фактора:
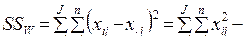
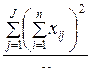 . (10.2)
. (10.2)
3. Вычисляется факториальная (межгрупповая) дисперсия SSb, связанная с влиянием градаций фактора:
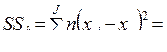
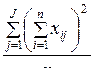
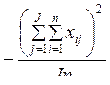 . (10.3)
. (10.3)
4. Вычисляется общая дисперсия SSc, которая соответствует сумме внутригрупповой и межгрупповой дисперсий: SSc = SSb + SSW. Общую дисперсию можно также вычислить по следующей формуле:
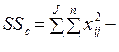
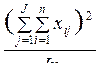 . (10.4)
. (10.4)
5. Вычисляется показатель силы влияния 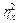 как отношение межгрупповой дисперсии к общей:
как отношение межгрупповой дисперсии к общей:
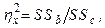 (10.5)
(10.5)
6. Определяется число степеней свободы:
а) число степеней свободы, связанное с межгрупповой дисперсией: n1 = J - 1;
б) число степеней свободы, связанное с внутригрупповой дисперсией: n2 = J (n - 1).
7. Вычисляется показатель достоверности влияния:
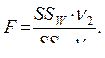 (10.6)
(10.6)
Достоверность определяется по критерию Фишера для определенного уровня значимости по соответствующей таблице. Стандартное значение Fст. определяется на перекресте столбца, соответствующего значению n1 и строки, соответствующей значению n2. Вывод о том, что влияние фактора статистически значимо, принимается, если F ³ Fст.
Для удобства работы с переменными рекомендуется пользоваться рабочей таблицей представления данных (табл. 10.4):
Таблица 10.4
| 1 | 2 | ... | J | 1 | 2 | ... | J |
| x11 x21 . . . xn1 | x12 x22 . . . xn2 | ... ... ... ... ... ... | x1J x2J . . . xnJ | x112 x212 . . . xn12 | x122 x222 . . . xn22 | ... ... ... ... ... ... | x1J2 x2J2 . . . xnJ2 |
Для вычисления промежуточных значений удобно пользоваться таблицей следующего вида (табл. 10.5):
Таблица 10.5
| №№ | Вычисляемый параметр | Последовательность вычислений |
| 1 |
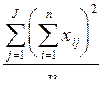
| xi (левая часть рабочей таблицы) суммируются по каждому столбцу и возводятся в квадрат: (x11 + x21 + ... + xn1)2 (x12 + x22 + ... + xn2)2 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . (x1J + x2J + ... + xnJ)2 Полученные квадраты суммируются и делятся на n. |
| 2 |
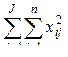
| Суммируются по столбцам квадраты чисел в правой части таблицы; полученные суммы квадратов суммируются построчно:
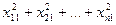 +
+
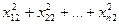 +
. . . . . . . . . . . . .
+
+
. . . . . . . . . . . . .
+
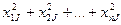
|
| 3 | SSW = (2) – (1) | Из результата (2) вычитается результат (1), получается внутригрупповая дисперсия SSW. |
| 4 | 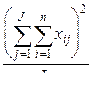
| Суммируются все варианты по столбцам и по строкам, возводятся в квадрат и делятся на общее число значений Jn. |
| 5 | SSb = (1) – (4) | Из результата (1) вычитается результат (4), получается межгрупповая дисперсия SSb |
| 6 | SSC = (2) – (4) = (3) + (5) | Общую дисперсию SSC можно получить двумя путями - либо вычитанием результата (4) из результата (2), либо суммированием результатов (3) и (5), т. е. межгрупповой и внутригрупповой дисперсией. |
| 7 |
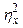 = (5)/(6) = (5)/(6)
| Показатель силы влияния вычисляется как отношение результатов (5) и (6), т.е. как отношение межгрупповой дисперсии к общей. |
| 8 | 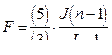
| Вычисляется отношение (5)/(3) и умножается на J(n-1)/(J-1), получается показатель достоверности влияния. |
Рассмотрим алгоритм вычислений на примере конкретной задачи.
Условие задачи
Исследовалось влияние возраста как фактора на уровень нейротизма, определяемого по тесту Айзенка. Тестирование проводилось в 4-х группах испытуемых разного возраста (соответственно, 7-й, 8-й, 9-й и 10-й классы) по 10 человек в каждой группе.
Получены следующие результаты (табл. 10.6):
Таблица 10.6
| Значения переменных | ||||
| Классы | 7-й | 8-й | 9-й | 10-й |
| Индивидуальные значения
| 16 | 9 | 21 | 9 |
| 6 | 14 | 17 | 13 | |
| 19 | 19 | 23 | 19 | |
| 10 | 16 | 12 | 14 | |
| 11 | 20 | 12 | 13 | |
| 13 | 18 | 17 | 12 | |
| 21 | 14 | 15 | 15 | |
| 14 | 22 | 21 | 23 | |
| 13 | 12 | 9 | 14 | |
| 11 | 17 | 9 | 17 | |
Задание
С помощью однофакторного дисперсионного анализа определить, является ли влияние возраста как фактора на уровень нейротизма статистически значимым.
Алгоритм решения
1. 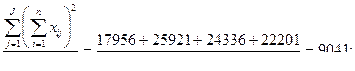
2. 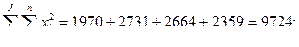
3. SSw = (2) – (1) = 9724 – 9041 = 683;
4. 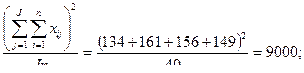
5. SSb = (1) – (4) = 9041 – 9000 = 41;
6. SSc = (2) – (4) = (3) + (5) = 9724 – 9000 = 683 + 41 = 724;
7. 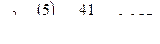
8. 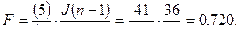
Ответ
F = 0,720 < F кр. = 2,86. Влияние возраста как фактора на уровень нейротизма не является статистически значимым.
Дата: 2018-11-18, просмотров: 667.