Коэффициент j используется в качестве меры связи в тех случаях, когда признаки х и у измеряются в дихотомической шкале наименований и могут принимать значения 0 или 1. Рассмотрим способы вычислений коэффициента на пример задачи.
Условие
Проведен социологический опрос, касающийся отношения населения к религии. Было опрошено 250 респондентов (100 мужчин и 150 женщин). По результатам опроса оказалось, что среди мужчин 40 верующих и 60 атеистов, а среди женщин 85 оказались верующими и 65 – атеистами.
Задание
Определить, существует ли связь между полом и отношением к религии. Определить знак и статистическую значимость коэффициента корреляции.
Решение
Введем необходимые обозначения:
- шкала х – пол (1 – мужчины, 0 – женщины);
- шкала у – отношение к религии (1 – верующий, 0 – атеист).
Задачу можно решить двумя различными способами:
1-й способ:
1. Составляем матрицу сопряженности признаков следующего вида:
|
| Признак х | |||
| 1 | 0 | Σ | ||
|
Признак у | 1 | a | b | a + b |
| 0 | с | d | c + d | |
| Σ | a + c | b + d | ||
2. Подставляем в матрицу полученные экспериментальные значения. В данном случае в качестве измеряемого признака служит число испытуемых, принимающее разные значения при сочетании шкал х и у. Так, в клетку а матрицы вносится число испытуемых, имеющих единицу по обеим шкалам, т. е число верующих мужчин; в клетку b – испытуемые, имеющие 0 по шкале х и 1 по шкале у (число верующих женщин) и т. д.
|
| Признак х | |||
| 1 | 0 | Σ | ||
|
Признак у | 1 | 40 | 85 | 125 |
| 0 | 60 | 65 | 125 | |
| Σ | 100 | 150 | ||
3. Используем формулу дихотомического коэффициента корреляции:
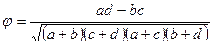(8.12)
4. Проводим вычисления:
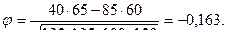
Интерпретация знака коэффициента корреляции состоит в том, что если он положителен, то 1 по х коррелирует с 1 по у, 0 по х коррелирует с 0 по у. Отрицательный коэффициент (как в нашем случае) свидетельствует о том, что 1 по х коррелирует с 0 по у, 0 по х коррелирует с 1 по у. Другими словами, женщины являются более верующими, а мужчины – более атеистичными.
По таблице критических значений дихотомического коэффициента корреляции (см. Приложение, табл. XVI) находим, что коэффициент является статистически значимым для 1-го уровня (φкр. = 0,13).
При отсутствии соответствующей таблицы можно воспользоваться следующим соотношением (для 1-го уровня значимости):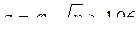 
и 
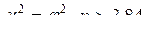
В нашем случае: z = 2,58 и χ2 = 6,64, т. е. вывод подтверждается.
Кроме того, в табл. VI Приложения можно определить статистическую значимость χ2 и для более высоких уровней (ν =1).
Вывод
Корреляция между полом и отношением к религии является статистически значимой, что можно констатировать с вероятностью 0,95.
2-й способ:
Обозначим: px – относительная доля испытуемых, имеющих единицу по х, qx = 1 – px – имеющих нуль по х; аналогично: py – доля испытуемых, имеющих единицу по у, qy = 1 – py – имеющих нуль по у; наконец, pxy - доля людей, имеющих единиц по x и по y.
Коэффициент j вычисляется по формуле:
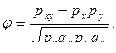(8.13)
В нашем примере: px = 100:250 = 0,40; qx = 1 – 0,40 = 0,60; py = 120:250 = 0,50; qy = 1 – 0,50 = 0,50; pxy = 40:250 = 0,16. Подставляя значения в формулу, получаем: φ = –0,163. Вывод подтверждается.
8. 8. Точечный бисериальный коэффициент корреляции (rpb)
Точечный бисериальный коэффициент корреляции используется тогда, когда одна переменная формирует дихотомическую шкалу наименований, другая – шкалу интервалов или шкалу отношений. Порядок вычислений коэффициента рассмотрим на примере следующей задачи.
Условие задачи
В группе испытуемых, протестированных по тесту Айзенка, обнаружено 15 экстравертов, из них 8 с высоким уровнем нейротизма (холерики) и 7 – с низким нейротизмом (сангвиники). Тест Спилбергера обнаружил у тех и других следующий уровень личностной тревожности (УЛТ):
Таблица 8.7
| Тип темперамента | Уровень личностной тревожности | |||||||
| Холерики | 42 | 44 | 40 | 38 | 43 | 37 | 41 | 42 |
| Сангвиники | 34 | 36 | 38 | 40 | 35 | 38 | 39 | |
Задание
Определить уровень связи и ее статистическую значимость между типом темперамента и уровнем личностной тревожности.
Решение
1. Учитывая, что шкала типов темперамента дихотомическая, а шкала УЛТ – интервальная, используем формулу для вычисления точечно-бисериальный коэффициент корреляции:
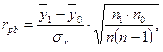(8.14)
где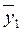 
и 
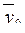, соответственно, средние значения переменных для двух интервальных шкал, т. е. средние значения УЛТ для холериков ( 
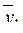)и сангвиников ( 
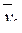); σу – стандартное отклонение для всей выборки; n1 и n0 – численность каждой из сравниваемых выборок и n = n1 + n0 – общее число испытуемых.
2. Определяем промежуточные значения: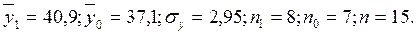 
3. Проводим вычисления: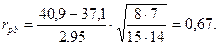 
4. Определяем число степеней свободы: ν = (n1 – 1) + (n0 – 1) = 13.
5. В табл. XIII Приложений находим критические значения коэффициента корреляции (специальной таблицы для rpb не существует): rкр. = 0,51 (β1 = 0,95) и 0,64 (β2 = 0,99). rpb > rкр.. В данном случае можно воспользоваться и табл. XV: как можно видеть, для статистической значимости коэффициента, равного 0,67, достаточно 9 испытуемых для 1-го и 13 – для 2-го уровня (в нашем примере n =15).
Вывод. Корреляция между типом темперамента и уровнем личностной тревожности статистически значима для 1-го и 2-го уровней.
8. 9. Рангово-бисериальный коэффициент корреляции (rrb)
Рангово-бисериальный коэффициент корреляции используется в том случае, когда одна переменная измеряется в дихотомической шкале наименований, другая представлена порядковой шкалой. В качестве примера рассмотрим следующую задачу.
Условие задачи
10 подростков (из них 6 мальчиков и 4 девочки) были проранжированы на предмет внешних проявлений агрессивности по отношению к своим сверстникам. Ранги распределились следующим образом (табл. 8.8):
Таблица 8.8
| Пол | Ранг агрессивности | |||||
| Мальчики | 1 | 2 | 4 | 6 | 7 | 8 |
| Девочки | 3 | 5 | 9 | 10 | ||
Задание
Определить, существует ли связь между полом и агрессивностью в группе исследуемых подростков.
Решение
1. Учитывая, что мы имеем дело с дихотомической и ранговой шкалами, используем рангово-бисериальный коэффициент корреляции:
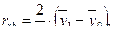(8.15)
где 
и 
- средние ранговые значения, n – численность выборки.
2. Проводим вычисления:
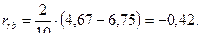
ν = (n 1 – 1) + (n 0 – 1) = 8; rкр. = 0,63 (β1 = 0,95) и 0,77 (β2 = 0,99). rpb > rкр.
Вывод
Корреляция между полом и агрессивностью для данной выборки испытуемых не является статистически значимой.
Выбор меры связи
Для того, чтобы сделать адекватный выбор коэффициента корреляции для решения той или иной задачи, необходимо правильно определить тип шкалы, которым представлена та или иная переменная. Возможные сочетания различных типов шкал и соответствующие им коэффициенты корреляции представлены в табл. 8.9.
Таблица 8.9
| Типы сравниваемых шкал |
Коэффициент корреляции | |
| 1 | 2 | |
| Дихотомическая | Дихотомическая | Дихотомический (φ) |
| Дихотомическая | Порядковая (ранговая) | Рангово-бисериальный (rrb) |
| Дихотомическая | Интервальная | Точечно-бисериальный (rpb) |
| Ранговая | Ранговая | Коэффициент Пирсона (rxy) Коэффициент Спирмена (rs) Коэффициент Кендалла (τ) |
| Ранговая | Интервальная | Коэффициент Пирсона (rxy) |
| Интервальная | Интервальная | Коэффициент Пирсона (rxy) |
В некоторых случаях (как, правило, для упрощения обработки результатов) используют преобразования одной шкалы в другую. Тем не менее, эти преобразования могут быть сделаны только в одном направлении: интервальная → ранговая → дихотомическая шкала (но не наоборот). Порядок преобразования интервальной шкалы в ранговую был рассмотрен нами ранее (критерий Манна-Уитни, подраздел 7.3). В то же время напомним, что такое преобразование существенно обедняет информацию о поведении переменной и может использоваться лишь в случае необходимости.
Матрицы корреляций
Матрицы корреляций (иначе, корреляционные матрицы) используются в тех случаях, когда нам необходимо определить попарные связи между большим количеством переменных. Так, если мы имеем дело только с двумя переменными x и y, для определения связи между ними достаточно одного коэффициента связи (rxy). При наличии трех переменных (x, y, z) необходимо использовать уже 3 коэффициента: rxy, rxz и ryz. Определение связи между 4 переменными предполагает вычисление 6-и, между 5 переменными – 10-и коэффициентов корреляции и т. д. Корреляционные матрицы служат для упорядочивания и наглядного представления этих значений. Общий вид корреляционной матрицы при использовании 6 измеряемых признаков (обозначим их латинскими буквами от A до F) представлен в табл. 8.10.
Таблица 8.10
| Переменные | A | B | C | D | E | F |
| A | 1 | |||||
| B | 1 | |||||
| C | 1 | |||||
| D | 1 | |||||
| E | 1 | |||||
| F | 1 |
Надо ли заполнять всю площадь матрицы? Скорее всего, это необязательно. В данном случае необходимо руководствоваться двумя правилами:
1. rxx = 1. Другими словами, корреляция переменной сама с собой равна единице. Таким образом, главная диагональ матрицы автоматически будет представлена единицами и вычислений не требует.
2. rxy = ryx, т. е. левая нижняя и правая верхняя половины матрицы будут зеркально отражать друг друга (так, rAD = rDA и т. д.). Поэтому заполняется лишь одна (как правило, правая верхняя) половина матрицы.
Руководствуясь этими правилами, легко вычислить общее число коэффициентов корреляции для упорядочения переменных. Рассуждаем следующим образом: для N переменных общая площадь матрицы будет составлять N2; вычитая число значений главной диагонали матрицы N и деля оставшееся значение пополам, получаем (N2 – N)/2 = N(N – 1)/2. Так, если мы имеем 15 переменных, то число возможных связей между ними будет составлять 15·(15 – 1)/2 = 105.
При большом числе переменных также такие упорядоченные матрицы корреляций могут оказаться довольно громоздкими. Для наглядности представления рекомендуется пользоваться «редуцированными» матрицами, т. е. удалять из них все коэффициенты корреляции, не достигающие критического значения. Работа с такими матрицами более удобна и экономична.
Задачи по теме
Задача 8.1
Условие задачи
Согласно концепции Г.Айзенка экстра-интроверсия и нейротизм являются независимыми переменными, не связанными между собой.
Задание
Проверить исходную предпосылку Г.Айзенка, используя данные, полученные на 50 испытуемых, протестированных по тесту Айзенка (ЭИ – показатели экстра-интроверсии, Н – показатели нейротизма).
| № | ЭИ | Н | № | ЭИ | Н | № | ЭИ | Н | № | ЭИ | Н | № | ЭИ | Н |
| 1 2 3 4 5 6 7 8 9 10 | 7 13 12 15 14 16 11 8 9 18 | 18 15 20 9 20 15 15 20 15 9 | 11 12 13 14 15 16 17 18 19 20 | 7 9 10 9 6 17 12 9 17 8 | 18 10 12 15 20 12 8 13 8 12 | 21 22 23 24 25 26 27 28 29 30 | 13 18 5 16 13 15 7 16 16 14 | 10 17 11 23 16 18 7 20 9 11 | 31 32 33 34 35 36 37 38 39 40 | 13 19 5 7 6 11 17 11 7 14 | 18 8 11 14 8 10 11 12 15 10 | 41 42 43 44 45 46 47 48 49 50 | 9 11 18 18 15 10 8 13 17 12 | 6 4 18 9 21 11 5 15 16 15 |
Задача 8. 2
Условие задачи
У 50 испытуемых, протестированных по тесту Шмишека, определялся уровень гипертимности и дистимности (черты, связанные с преобладающим настроением, доминирующим эмоциональным «фоном»). Теоретически эти черты являются противоположными: гипертимность характеризует повышенное настроение, преобладание положительных эмоций, дистимность – наоборот. В то же время определение этих качеств основывается на ответах испытуемых на разные, по существу, вопросы.
Экспериментальные данные:
| № | Гип | Дис | № | Гип | Дис | № | Гип | Дис | № | Гип | Дис | № | Гип | Дис |
| 1 2 3 4 5 6 7 8 9 10 | 4 3 2 1 5 3 3 2 3 5 | 2 0 5 3 5 3 3 1 4 0 | 11 12 13 14 15 16 17 18 19 20 | 0 2 1 2 1 1 3 6 1 4 | 5 1 7 2 5 1 3 1 3 1 | 21 22 23 24 25 26 27 28 29 30 | 4 5 5 1 6 3 2 3 2 5 | 1 0 1 5 4 4 3 5 3 0 | 31 32 33 34 35 36 37 38 39 40 | 4 2 2 2 1 0 5 2 1 1 | 4 1 1 4 3 3 0 3 2 4 | 41 42 43 44 45 46 47 48 49 50 | 2 5 3 5 4 3 5 4 4 4 | 2 2 2 0 5 3 0 2 2 3 |
Задание
Подтвердить или опровергнуть версию о противоположности двух психологических черт – гипертимности и дистимности.
Задача 8. 3
Условие задачи
У 10 испытуемых измерялся уровень нейротизма по тесту Айзенка и импульсивность по тесту Шмишека. Получены следующие результаты:
| Испытуемый | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Нейротизм | 12 | 19 | 11 | 13 | 20 | 17 | 8 | 15 | 18 | 16 |
| Импульсивность | 3 | 5 | 4 | 3 | 7 | 4 | 2 | 5 | 7 | 3 |
Задание
Определить наличие или отсутствие связи между нейротизмом и импульсивностью.
Задача 8. 4
Условие задачи
По результатам областных олимпиад по биологии и математике определились 10 школьников, занявших призовые места по обоим предметам. При этом места по биологии (х) и математике (у) распределились следующим образом:
| № | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| x | 7 | 1 | 10 | 3 | 6 | 8 | 2 | 9 | 4 | 5 |
| y | 1 | 7 | 9 | 2 | 4 | 8 | 3 | 10 | 5 | 6 |
Задание
Определить, существует ли связь между знаниями призеров-школьников по биологии и математике.
Задача 8. 5
Условие задачи
У 20 старшеклассников определялся коэффициент интеллекта (IQ), в соответствии с которым школьники были проранжированы в порядке его убывания (каждому из них был присвоен ранг от 1 до 20). Те же школьники были проранжированы по среднему баллу текущей успеваемости. Получены следующие результаты:
| Ранг IQ | Ранг усп. | Ранг IQ | Ранг усп. | Ранг IQ | Ранг усп. | Ранг IQ | Ранг усп. |
| 1 2 3 4 5 | 5 11 1 12 6 | 6 7 8 9 10 | 16 13 2 17 14 | 11 12 13 14 15 | 10 18 7 3 15 | 16 17 18 19 20 | 8 19 4 20 9 |
Задание
Определить, существует ли связь между коэффициентом интеллекта и успеваемостью для данной группы школьников.
Задача 8. 6
Условие задачи:
Опрос учащихся выпускного класса одной из средних школ (32 человека, из них 14 юношей и 18 девушек) показал, что среди опрошенных 9 юношей и 5 девушек регулярно посещают дискотеку.
Задание
Определить уровень и достоверность корреляции между полом и посещением дискотеки.
Задача 8. 7
Условие задачи
У 56 испытуемых (28 юношей и 28 девушек) определся показатель экстра-интроверсии по тесту Айзенка. Получены следующие результаты:
| №№ | Ю | Д | №№ | Ю | Д | №№ | Ю | Д | №№ | Ю | Д |
| 1 2 3 4 5 6 7 | 13 15 14 16 11 8 9 | 7 12 7 6 17 17 13 | 8 9 10 11 12 13 14 | 18 9 10 9 12 9 8 | 18 15 16 16 14 13 19 | 15 16 17 18 19 20 21 | 5 16 13 7 6 17 7 | 5 7 11 11 11 18 15 | 22 23 24 25 26 27 28 | 14 9 18 10 8 13 17 | 12 10 10 14 16 3 8 |
Задание.
Определить, существует ли связь между полом и уровнем экстра-интроверсии для данной выборки испытуемых.
Задача 8. 8
Условие задачи
У 20 испытуемых определялся уровень личностной тревожности (УЛТ) по тесту Спилбергера, а также уровень нейротизма и экстра-интроверсии по тесту Айзенка. Определение типа темперамента по Айзенку выявило среди 20 испытуемых 9 холериков, 6 сангвиников, 3 флегматика и 2 меланхолика.
Значения УЛТ у разных испытуемых распределились следующим образом.
| Тип темперамента | Уровень личностной тревожности | ||||||||
| Холерики | 38 | 41 | 40 | 37 | 42 | 39 | 40 | 43 | 42 |
| Сангвиники | 34 | 38 | 36 | 40 | 35 | 37 | |||
| Флегматики | 35 | 39 | 37 | ||||||
| Меланхолики | 42 | 41 | |||||||
Задание
Определить, существует ли связь между типом темперамента и уровнем личностной тревожности у холериков и сангвиников.
Задача 8. 9
Условие задачи
У 10 испытуемых обоего пола определялись показатели импульсивности и экзальтированности по тесту Шмишека. Получены следующие результаты:
| Испытуемый | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Импульсивность | 2 | 4 | 7 | 6 | 8 | 5 | 7 | 6 | 4 | 2 |
| Экзальтированность | 1 | 3 | 4 | 2 | 3 | 3 | 1 | 2 | 4 | 1 |
Задание
Определить, существует ли корреляция между двумя показателями акцентуаций (импульсивностью и экзальтированностью) для данной выборки испытуемых.
Задача 8. 10
Условие задачи
10 юношей и 10 девушек выпускного класса средней школы получили следующие средние баллы аттестата:
| № пп. | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Юноши | 3,6 | 4,1 | 4,8 | 3,2 | 3,9 | 4,3 | 3,8 | 4,2 | 3,4 | 4,7 |
| Девушки | 4,8 | 4,3 | 4,4 | 3,3 | 4,2 | 3,8 | 4,9 | 4,1 | 4,0 | 3,6 |
Задание
Определить уровень и достоверность корреляции между полом и средним баллом выпускного аттестата.
З а д а ч а 8. 11
Условие задачи
В спортивных состязаниях учащихся средней школы определилось 10 призеров (6 в одном выпускном классе и 4 в другом). Призовые места определились следующим образом: в 11-а классе - 1-е, 3-е, 4-е, 6-е, 8-е и 9-е; в 11-б - 2-е, 5-е, 7-е и 10-е место.
Задание
1. Определить учащиеся какого класса выступили на соревнованиях более успешно.
2. Определить коэффициент корреляции между выпускным классом и призовыми местами.
З а д а ч а 8. 12
Условие задачи
В исследовании, моделирующем деятельность авиадиспетчера, группа испытуемых (10 человек) проходила подготовку перед началом работы на тренажере. При этом подсчитывалось число ошибок, допущенных при тренировке. Кроме того, у каждого испытуемого определялись показатели вербального и невербального интеллекта по методике Д. Векслера. Получены следующие результаты:
| Испытуемые | Количество ошибок | Вербальный IQ | Невербальный IQ |
| 1 2 3 4 5 6 7 8 9 10 | 29 54 13 8 14 26 9 20 2 17 | 131 132 121 127 136 124 134 136 132 136 | 106 90 95 116 127 107 104 102 111 99 |
Задание
Определить, связано ли количество ошибок, допущенных испытуемыми в тренировочной сессии, с показателями вербального и невербального интеллекта по Векслеру.
З а д а ч а 8. 13
Условие задачи
В выборке петербуржцев в возрасте от 20 до 78 лет (31 мужчина, 46 женщин) предлагалось ответить на вопрос: «Какой уровень развития каждого из перечисленных ниже качеств необходим для депутата?». Оценка производилась по 10-балльной шкале. Кроме того, проводилась индивидуальная диагностика кандидатов с помощью Оксфордской системы экспресс-видеодиагностики (20-балльная шкала) по тому же набору личностных качеств, который предъявлялся выборке избирателей.
Задание
Определить, насколько депутат К-в соответствует эталону избирателей.
| №№ пп. | Наименование качеств | Усредненные эталонные оценки избирателей | Индивидуальные показатели депутата К-ва |
| 1 | Общий уровень культуры | 8,64 | 15 |
| 2 | Обучаемость | 7,89 | 7 |
| 3 | Логика | 8,38 | 12 |
| 4 | Способность к творчеству нового | 6,97 | 5 |
| 5 | Самокритичность | 8,28 | 14 |
| 6 | Ответственность | 9,56 | 18 |
| 7 | Самостоятельность | 8,12 | 13 |
| 8 | Энергия, активность | 8,41 | 17 |
| 9 | Целеустремленность | 8,00 | 19 |
| 10 | Выдержка, самообладание | 8,71 | 9 |
| 11 | Стойкость | 7,74 | 16 |
| 12 | Личностная зрелость | 8,10 | 11 |
| 13 | Порядочность | 9,02 | 12 |
| 14 | Гуманизм | 7,89 | 10 |
| 15 | Умение общаться с людьми | 8,74 | 8 |
| 16 | Терпимость к чужому мнению | 7,84 | 6 |
| 17 | Гибкость поведения | 7,67 | 4 |
| 18 | Способность производить благоприятное впечатление | 7,23 | 8 |
З а д а ч а 8. 14
Условие задачи
Клинический психолог и логопед совместно проранжировали 20 детей по двум переменным: х – эмоциональная устойчивость (1 – наибольшая, 20 – наименьшая), y – степень заикания (1 – наименьшая, 20 – наибольшая). Полученные данные представлены в таблице.
| Ребенок | Эмоциональная устойчивость | Степень заикания | Ребенок | Эмоциональная устойчивость | Степень заикания |
| 1 2 3 4 5 6 7 8 9 10 | 1 2 3 4 5 6 7 8 9 10 | 5 1 8 3 2 10 13 6 14 12 | 11 12 13 14 15 16 17 18 19 20 | 11 12 13 14 15 16 17 18 19 20 | 4 18 16 15 19 9 7 17 20 11 |
Задание
Определить, существует ли связь между степенью заикания и эмоциональной устойчивостью.
З а д а ч а 8. 15
В таблице приведены результаты тестирования по MMPI одного испытуемого (мужчина, студент), проведенные с интервалом 2,5 года. Можно ли говорить об изменении профиля психологических черт у данного испытуемого?
| №№ шкалы | Название шкалы | 1-е тестирование | 2-е тестирование |
| 1 | Ипохондрия | 41,5 | 43,1 |
| 2 | Депрессия | 70,3 | 59,8 |
| 3 | Истерия | 64,2 | 58,8 |
| 4 | Психопатия | 71,8 | 71,8 |
| 5 | Мужественность – женственность | 61,4 | 57,1 |
| 6 | Паранойя | 61,8 | 58,9 |
| 7 | Психастения | 68,9 | 56,6 |
| 8 | Шизофрения | 76,5 | 63,0 |
| 9 | Гипомания | 51,5 | 46,5 |
| 10 | Социальная интроверсия | 54,2 | 46,8 |
Задача 8.16
Опираясь на данные авторов Hand-test’а (Курбатова, Муляр, 1995), подтвердите или опровергните утверждение о том, что соотношение ответов разных категорий различно в сопоставляемых группах испытуемых (табл.).
| Категории ответов | «Норма» | Невро- тики | Шизо-френики | Заключен-ные | Эпилеп-тики |
| Agg (агрессия) | 1,8 | 1,1 | 2,3 | 1,4 | 4,0 |
| Dir (директивность) | 2,1 | 1,8 | 1,7 | 1,5 | 2,7 |
| F (страх) | 0,6 | 0,5 | 0,7 | 0,01 | 0 |
| Aff (аффектация) | 2,4 | 1,2 | 1,1 | 0,5 | 0,6 |
| Com (коммуникация) | 2,1 | 1,3 | 0,3 | 0,4 | 0,6 |
| Dep (зависимость) | 1,8 | 1,3 | 1,1 | 0,5 | 1,0 |
| Ex (эксгибиционизм) | 1,2 | 0,5 | 0,4 | 0,3 | 0,2 |
| Crip (калечность) | 1,0 | 0,5 | 0,5 | 0,7 | 1,0 |
| Act (активные безличные ответы) | 8,3 | 4,0 | 4,0 | 3,5 | 7,4 |
| Pas (пассивные безличные ответы) | 2,2 | 2,1 | 2,0 | 0,3 | 1,8 |
| Des (описание) | 0,8 | 0,8 | 0,6 | 0,2 | 0 |
З а д а ч а 8. 17
Различается ли соотношение ответов, полученных в Hand-test’е, в мужской (75 человек от 20 до 40 лет, высшее гуманитарное образование) и женской (133 человека от 20 до 40 лет, высшее образование) выборках, согласно статистическим нормам, приведенным Т.Н. Курбатовой (1995).
| Категории ответов | Мужчины | Женщины |
| Agg (агрессия) | 2,3 | 1,5 |
| Dir (директивность) | 2,2 | 1,9 |
| Aff (аффектация) | 2,3 | 1,9 |
| Com (коммуникация) | 2,5 | 2,3 |
| Dep (зависимость) | 1,0 | 0,6 |
| F (страх) | 0,8 | 0,7 |
| Ex (эксгибиционизм) | 1,0 | 1,1 |
| Crip (калечность) | 0,5 | 0,6 |
| Des (описание) | 1,2 | 1,2 |
| Ten (напряжение) | 0,5 | 0,6 |
| Act+Pas (активные и пассивные безличные ответы) | 6,4 | 6,3 |
Задача 8.18
Выяснить, совпадает ли структура ценностных ориентаций, выявленная тестом Рокича у юношей и девушек (студенты-первокурсники УрГУ, 1998 год поступления)?
Результаты ранжирования ценностей студентами
(цифры в таблице соответствуют среднему рангу по выборке: Rю – средний ранг для юношей, Rд – средний ранг для девушек)
| Терминальные ценности | Rю | Rд | Инструментальные ценности | Rю | Rд |
| Активная деятельная жизнь | 9,8 | 7,5 | Аккуратность | 8,4 | 10,0 |
| Жизненная мудрость | 7,4 | 9,9 | Воспитанность | 7,1 | 8,4 |
| Здоровье | 4,8 | 5,7 | Высокие запроосы | 12,7 | 13,5 |
| Интересная работа | 8,3 | 8,3 | Жизнерадостность | 8,3 | 7,4 |
| Красота природы и искусства | 11,1 | 12,3 | Исполнительность | 11,7 | 11,7 |
| Любовь | 7,6 | 5,7 | Независимость | 6,5 | 8,2 |
| Материально обеспеченная жизнь | 8,4 | 9,9 | Непримиримость к недостаткам | 14,3 | 16,1 |
| Наличие хороших и верных друзей | 7,3 | 6,5 | Образованность | 5,8 | 5,8 |
| Общественное признание | 11,1 | 11,3 | Ответственность | 10,1 | 7,5 |
| Познание | 9,5 | 9,6 | Рационализм | 9,7 | 10,6 |
| Продуктивная жизнь | 12,5 | 10,2 | Самоконтроль | 8,9 | 8,4 |
| Развитие | 8,8 | 9,8 | Смелость в отстаивании своего мнения | 8,5 | 9,4 |
| Развлечения | 11,8 | 13,6 | Твердая воля | 9,1 | 8,6 |
| Свобода | 7,6 | 8,5 | Терпимость | 10,1 | 8,7 |
| Счастливая семейная жизнь | 12,1 | 9,8 | Широта взглядов | 8,9 | 8,3 |
| Счастье других | 13,7 | 13,3 | Честность | 8,6 | 7,9 |
| Творчество | 11,6 | 12,1 | Эффективность в делах | 10,5 | 10,7 |
| Уверенность в себе | 8,0 | 7,0 | Чуткость | 11,7 | 9,8 |
З а д а ч а 8. 19
Условие задачи
С помощью цветового теста отношений (ЦТО) были исследованы несколько социальных стереотипов (Е.Ф. Бажин, А.М. Эткинд, 1985).
В таблице приведены усредненные ранговые ряды цветов в порядке их соответствия каждому социальному стереотипу. Обозначения цветов приведены в соответствии с тестом М. Люшера (1 – синий, 2 – зеленый, 3 – красный, 4 – желтый, 5 – фиолетовый, 6 – коричневый, 7 – черный, 0 – серый).
| Социальный стереотип | Последовательность Цветов | Социальный стереотип | Последовательность цветов |
| Друг Отшельник Клоун | 3 1 2 6 0 4 5 7 0 1 7 6 5 2 3 4 4 3 5 2 1 6 0 7 | Божий одуванчик Полковник Предатель | 4 6 5 2 0 1 3 7 3 1 7 2 6 5 0 4 7 5 0 6 1 2 4 3 |
Задание
Ориентируясь на приведенные данные, проанализировать, какие социальные стереотипы наиболее близки и наиболее далеки друг от друга.
раздел 9.
МЕРЫ ЗАВИСИМОСТИ
Основные понятия
Напомним, что корреляционная связь между переменными не всегда означает связь причинно-следственную. Другими словами, если переменные связаны друг с другом, то на этом основании мы не можем сделать вывод о том, что одна из них зависит от другой. Так, например, на основании антропометрических измерений установлена положительная корреляция между ростом и весом субъектов в многочисленной выборке испытуемых. Однако мы не можем сказать на этот счет, что вес зависит от роста или, наоборот, рост зависит от веса. Скорее всего, и то и другое зависит от третьей переменной – в данном случае от конституциональных особенностей человека, задаваемых генетическими факторами. Совершенно аналогично, обнаружив корреляцию между уровнем нейротизма и личностной тревожности, мы не можем говорить, что они находятся в причинно-следственной зависимости друг от друга.
О зависимости [y = f (x)] можно говорить лишь в тех случаях, когда х – независимая переменная, принимающая фиксированные значения, которые, как правило, задаются экспериментатором, а у может принимать любые значения так, что каждому хi соответствует определенное уi.
Чаще всего с различными формами зависимости приходится иметь дело в психофизике. Так, сенсорные сигналы, предъявляемые экспериментатором, являются независимыми величинами, а ответы испытуемого (суждения, оценки) – зависимыми от физических характеристик сигнала. С разными типами зависимостей приходится сталкиваться и в возрастной, и в социальной, и в клинической психологии, а также в других областях.
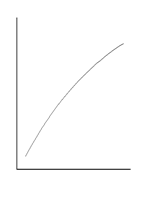
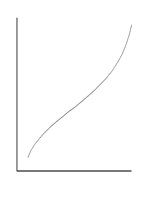
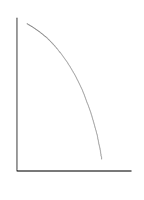
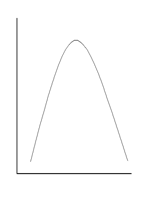
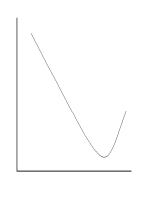
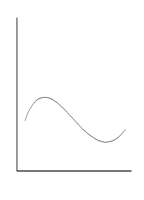
Различают монотонные и немонотонные формы зависимости. Если функция y закономерно возрастает или убывает с увеличением значения аргумента x, то такую зависимость называют монотонной (рис. 9.1 а, б, в). В случае немонотонной зависимости имеется одна или несколько точек (экстремумов), в которых производная dy/dx меняет свой знак на обратный (рис. 9.1 г, д, е).
Формы монотонной зависимости
 
|  
| 
|
а б в
Формы немонотонной зависимости
| 
| 
|
г д е
Рис. 9.1. Графическое изображение различных форм зависимости (пояснения в тексте)
Как правило, в психологических исследованиях редко используются методы математического описания немонотонных форм зависимости (при необходимости для этой цели можно использовать дифференциальные уравнения). Обычно констатируется сам факт, что наблюдается именно такая форма зависимости. Например, зависимость числа ошибок при решении интеллектуальной задачи от уровня эмоциональной напряженности имеет приблизительно U-образный вид (рис. 9.1 д). В этом случае наименьшее число ошибок соответствует среднему уровню тревожности. Если же исследовать зависимость эффективности совместного решения проблемы (так называемый «мозговой штурм») от численности рабочей группы, то она, как правило, имеет вид инвертированной U-образной кривой (рис. 9.1 г) и т. д.
Если экспериментальная кривая имеет вид монотонной зависимости, то можно попытаться описать ее соответствующей математической функцией. Для этих целей в качестве предварительного метода можно использовать метод подбора координат. Этот метод позволяет в первом приближении установить, в какой системе координат исследуемая кривая является наиболее линейной. Так, например, логарифмическая зависимость y = k×log x примет вид линейной функции в полулогарифмических координатах y = f (log x), степенная функция y = k×x n становится линейной в двойных логарифмических координатах log y = f (log x) и т. д. Анализ же линейной зависимости и ее математическое описание достаточно просты и предполагают использование метода наименьших квадратов.
Поскольку экспериментальные точки (значения переменной, полученные в опыте) всегда имеют определенный разброс и почти никогда в точности не ложатся на прямую линию, отдать предпочтение той или иной математической функции иногда затруднительно. В таких случаях предпочтение отдается той форме зависимости, где сумма квадратов отклонений экспериментальных точек от теоретической функции минимальна.
Дата: 2018-11-18, просмотров: 595.
