Критерий Колмогорова – Смирнова основан на том же принципе, что и критерий χ2 Пирсона, но предполагает сопоставление накопленных частот экспериментального и теоретического распределений. Вычисляется как отношение максимальной разности (без учета знака) между теоретической и экспериментальной накопленной частотой к корню квадратному из численности выборки: (6.6)
Для вычисления l также можно воспользоваться таблицами теоретических частот 8- и 16-классового распределения. Рассмотрим алгоритм вычислений критерия Колмогорова на примере предыдущей задачи (табл. 6.3).
Таблица 6.3
| Границы класса | Экспериментальные частоты | Накопленные частоты | d | |
| Fэ | Fт | |||
| 1 | 2 | 3 | 4 | 5 |
| – 4 σ ÷ – 3 σ – 3 σ ÷ – 2 σ – 2 ÷ – σ – σ ÷ 0 0 ÷ σ σ ÷ 2 σ 2 ÷ 3 σ 3 ÷ 4 σ | 0 2 16 34 30 17 1 0 | 0 2 18 52 82 99 100 100 | 0,13 2,28 15,87 50,00 84,13 97,72 99,87 100 | 0,13 0,28 2,13 2,00 2,13 1,28 0,13 0 |
Столбцы 1 и 2 аналогичны таковым в предыдущей таблице. Столбец 3 соответствует экспериментальным частотам, накопленным путем суммирования частот от 1-го до 8-го класса. Теоретические накопленные частоты взяты из табл. III Приложения. Максимальная разность между экспериментальной и теоретической накопленными частотами (столбец 5) соответствует 2,13. Проводим соответствующие вычисления:
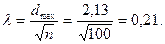
Для определения соответствия экспериментального распределения теоретическому по критерию Колмогорова можно воспользоваться следующим правилом. Если l < 0,52, делается вывод о соответствии распределений для уровня значимости 0,95. При l > 1,36 распределение достоверно отличается от нормального. При значениях же l от 0,52 до 1,36 (интервал неопределенности) можно определить вероятность соответствия экспериментального распределения теоретическому по табл. VII Приложения.
Вывод
Полученное нами значение λ = 0,21 < 0,52, следовательно, по критерию Колмогорова экспериментальное распределение соответствует нормальному с вероятностью 0,95.
Для определения соответствия эмпирического распределения теоретическому (нормальному) распределению можно воспользоваться и другим способом, который зачастую дает более точные результаты, поскольку не ограничен числом классов. Этот способ будет нами рассмотрен на примере той же задачи.
Порядок вычислений приводится в табл. 6.4.
1. В столбце 1 таблицы фиксируем значения xi (уровень нейротизма).
2. Переводим значения xi в меру z Пирсона по формуле: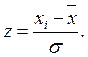 
3. Ориентируясь на условие задачи, вносим экспериментальные частоты в столбец 3.
4. По значениям столбца 3 вычисляем накопленные экспериментальные частоты и фиксируем их в столбце 4.
5. По значениям z Пирсона определяем теоретические накопленные частоты, для чего используем табл. V Приложений.
6. Вычисляем критерий d, сравнивая между собой экспериментальные (столбец 4) и теоретические частоты по формуле: d = │Fэксп. – Fтеор.│.
7. Вычисляем критерий λ Колмогорова по стандартной формуле.
Ответ
λ = 7,57:10 = 0,76 (столбец 6 таблицы), что соответствует интервалу неопределенности 0,52 ÷ 1,36.
С целью устранения случайных факторов используем процедуру интервальной нормализации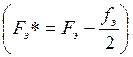 
(столбец 7) и повторно вычисляем критерий λ:
λ* = 4,64 : 10 = 0,46 (столбец 8 таблицы).
Общий ответ
Эмпирическое распределение соответствует теоретическому (нормальному) распределению.
Таблица 6.4
| xi | Z | fэ | Fэ | Fт | d | Fэ* | d * |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 | -3,2 -2,9 -2,7 -2,4 -2,2 -1,9 -1,6 -1,4 -1,1 -0,8 -0,6 -0,3 0 0,2 0,5 0,7 1,0 1,3 1,5 1,8 2,1 2,3 2,5 2,8 | 0 0 0 0 2 3 3 4 6 8 9 7 10 8 9 9 8 6 4 3 1 0 0 0 | 0 0 0 0 2 5 8 12 18 26 35 42 52 60 69 78 86 92 96 99 100 100 100 100 | 0,07 0,18 0,34 0,82 1,40 2,88 5,49 8,08 13,57 21,19 27,43 38,21 50,00 57,92 69,14 75,80 84,13 90,31 93,31 96,40 98,21 98,92 99,37 99,75 | 0,07 0,18 0,34 0,82 0,60 2,12 2,51 3,92 4,43 4,81 7,57 3,79 2,00 2,08 0,14 2,20 1,87 1,69 2,69 2,60 1,79 1,08 0,63 0,25 | 0 0 0 0 1 3,5 6,5 10 15 22 30,5 38,5 47 56 64,5 73,5 82 89 94 97,5 99,5 100 100 100 | 0,07 0,18 0,34 0,82 0,40 0,62 1,01 1,92 1,43 0,81 3,07 0,29 3,00 1,92 4,64 2,30 2,13 1,31 0,69 1,10 1,29 1,08 1,63 0,25 |
Равномерное распределение
В ряде случаев психологу приходится иметь дело с равномерным распределением, когда варьирующая величина (переменная) приблизительно с равной вероятностью принимает любое значение в определенном фиксированном диапазоне от xmin до xmax . Пример такого распределения приводится на рис. 6.5.
Рис. 6.5. Графическое выражение теоретического равномерного распределения (пояснения в тексте)
Примером равномерного распределения может служить распределение испытуемых по квантилям, поскольку в каждом интервале квантильной шкалы частоты встречаемости признака одинаковы.
Работа с равномерным распределением достаточно проста. Учитывая, что общая площадь распределения соответствует Р = 1, вероятность события в интересующем нас диапазоне x1 ¸ x2 равна отношению ширины этого диапазона (размаха вариаций) x2 - x1 к общему (xmax ¸ xmin). Для сравнения экспериментального распределения с теоретическим можно использовать критерий хи-квадрат, а при достаточном количестве эмпирических частот и критерий Колмогорова. Рассмотрим использование этих критериев на двух примерах.
Пример 1
Можно априорно предположить, что число людей, обладающих одним из четырех основных типов темперамента (холерики, сангвиники, флегматики и меланхолики) приблизительно одинаково. Для проверки этой гипотезы проведено тестирование по тесту-опроснику Айзенка 100 взрослых испытуемых. Тип темперамента определялся у них по соотношению показателей экстраверсии и нейротизма.
Было получено следующее распределение испытуемых по типам темперамента: холерики – 22 человека, сангвиники – 36, флегматики – 13 и меланхолики – 29 человек.
Задача состоит в том, чтобы либо принять, либо отвергнуть изначальную гипотезу (нуль-гипотезу) о равномерности распределения людей по типам темперамента.
Для решения задачи можно составить таблицу, аналогичную той, которая использовалась для оценки согласия эмпирического распределения с нормальным по критерию хи-квадрат (см. табл. 6.5).
Таблица 6.5
| Тип темперамента | Частота | (fэксп - fтеор )2 fтеор | |
| fэксп | fтеор | ||
| Холерики (экстраверты с высоким уровнем нейротизма) Cангвиники (эмоционально стабильные экстраверты) Флегматики (эмоционально стабильные интроверты) Меланхолики (интроверты с высоким уровнем нейротизма) | 22 36 13 29 | 25 25 25 25 | 0,36 4,84 5,76 0,64 |
В данном случае следует пояснить, что теоретические частоты рассчитываются, исходя из гипотезы о том, что распределение по типам темперамента является идеально равномерным.
Вычисление показателя c2 (сумма значений в последнем столбце таблицы) дает величину 11,6. При сравнении полученного значения со стандартным (табл. VI Приложений) следует иметь в виду, что для равномерного распределения число степеней свободы вычисляется как число групп (классов) разбиения минус единица: в нашем случае n = N – 1 = 3.
Полученное нами значение (c2 = 11,6) больше стандартных (критических) значений как для 1-го (c2ст = 7,815), так и для 2-го уровня значимости (c2ст = 11,345). Отсюда следует, что принять гипотезу о равномерности распределения людей по типам темперамента мы не можем. Другими словами, распределение статистически достоверно отличается от равномерного.
Примечания
4. Критерий c2 дает надежные результаты на выборках более 30 человек. На малых выборках (n ≤ 30) критерий может «пробуксовывать» и данные могут быть подвергнуты сомнению.
2. Если число градаций признака равно двум, в формулу вычисления c2 необходимо вводить соответствующую поправку (так называемую поправку на непрерывность): (fэксп - fтеор – 0,5)2
fтеор
Пример 2
Условие задачи
В выборке здоровых лиц мужского пола, студентов технических вузов в возрасте от 19 до 22 лет проводился тест М. Люшера в 8-цветном варианте. Установлено, что желтый цвет предпочитается испытуемыми чаще, чем отвергается (см. табл. 6.6).
Таблица 6.6
| Разряды | Позиции желтого цвета | Сумма | |||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ||
| Эмпирические частоты | 24 | 15 | 13 | 8 | 15 | 10 | 9 | 8 | 102 |
Вопрос
Можно ли утверждать, что распределение желтого цвета по восьми позициям у здоровых испытуемых отличается от равномерного распределения?
Решение
Для определения соответствия эмпирического распределения теоретическому (равномерному) можно использовать критерий Колмогорова. Для этого вносим экспериментальные данные в таблицу (табл. 6.7) и проводим стандартные вычисления.
Таблица 6.7
| Позиции желтого цвета | Частоты | Накопленные частоты |
d | ||
| fэксп | fтеор | Fэксп. | Fтеор. | ||
| 1 2 3 4 5 6 7 8 | 24 15 13 8 15 10 9 8 | 12,75 12,75 12,75 12,75 12,75 12,75 12,75 12,75 | 24 39 52 60 75 85 94 102 | 12,75 25,50 38,25 51,00 63,75 76,50 89,25 102 | 11,25 13,50 13,75 9,00 11,25 8,50 4,75 0 |
Отсюда: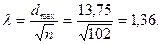 
Вывод
Экспериментальное распределение не соответствует теоретическому (равномерному) распределению.
Биномиальное распределение
В отличие от нормального и равномерного распределений, описывающих поведение переменной в исследуемой выборке испытуемых, биномиальное распределение используется для иных целей. Оно служит для прогнозирования вероятности двух взаимоисключающих событий в некотором числе независимых друг от друга испытаний. Классический пример биномиального распределения – подбрасывание монеты, которая падает на твердую поверхность. Равновероятны два исхода (события): 1) монета падает «орлом» (вероятность равна р) или 2) монета падает «решкой» (вероятность равна q). Если третьего исхода не дано, то p = q = 0,5 и p + q = 1. Используя формулу биномиального распределения, можно определить, например, какова вероятность того, что в 50 испытаниях (число подбрасываний монеты) последняя выпадет «орлом», предположим, 25 раз.
Для дальнейших рассуждений введем общепринятые обозначения:
n – общее число наблюдений;
i – число интересующих нас событий (исходов);
n – i – число альтернативных событий;
p – эмпирически определенная (иногда – предполагаемая) вероятность интересующего нас события;
q – вероятность альтернативного события;
Pn(i) – прогнозируемая вероятность интересующего нас события i по определенному числу наблюдений n.
Формула биномиального распределения:
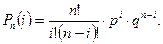(6.7)
В случае равновероятного исхода событий (p = q) можно использовать упрощенную формулу:
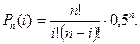(6.8)
Рассмотрим три примера, иллюстрирующие использование формул биномиального распределения в психологических исследованиях.
Пример 1
Предположим, что 3 студента решают задачу повышенной сложности. Для каждого из них равновероятны 2 исхода: (+) – решение и (-) – нерешение задачи. Всего возможно 8 разных исходов (2 3 = 8).
Вероятность того, что ни один студент не справится с задачей, равна 1/8 (вариант 8); 1 студент справится с задачей: P = 3/8 (варианты 4, 6, 7); 2 студента – P = 3/8 (варианты 2, 3, 5) и 3 студента – P =1/8 (вариант 1).
| Студент | Варианты исходов | |||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| A | + | + | + | + | - | - | - | - |
| B | + | + | – | – | + | + | - | - |
| C | + | - | + | - | + | - | + | - |
Пример 2
Предположим, 5 студентов выполняют интеллектуальный тест повышенной сложности. Правильное выполнение теста «+», неправильное «-». Каждый студент может иметь 2 возможных исхода (+ или -), причем вероятность каждого из этих исходов равна 0,5.
| Студенты | 1 | 2 | 3 | 4 | 5 |
| Возможные исходы | + - | + - | + - | + - | + - |
Необходимо определить вероятность того, что трое из 5 студентов успешно справятся с данной задачей.
Решение
Всего возможных исходов: 25 = 32.
Общее число вариантов 3(+) и 2(-) составляет
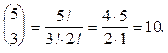
Следовательно, вероятность ожидаемого исхода равна 10/32 » 0,31.
Пример 3
Считается, что число экстравертов и интровертов в однородной группе испытуемых является приблизительно одинаковым.
Задание
Определить вероятность того, что в группе из 10 случайных испытуемых обнаружится 5 экстравертов.
Решение
1. Вводим обозначения: p = q = 0,5; n = 10; i = 5; P 10 (5) = ?
2. Используем упрощенную формулу (см. выше):
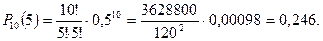
Вывод
Вероятность того, что среди 10 случайных испытуемых обнаружится 5 экстравертов, составляет 0,246.
Примечания
1. Вычисление по формуле при достаточно большом числе испытаний достаточно трудоемко, поэтому в этих случаях рекомендуется использовать таблицы биномиального распределения.
2. В некоторых случаях значения p и q можно задать изначально, но не всегда. Как правило, они вычисляются по результатам предварительных испытаний (пилотажных исследований).
3. В графическом изображении (в координатах Pn(i) = f (i)) биномиальное распределение может иметь различный вид: в случае p = q распределение симметрично и напоминает нормальное распределение Гаусса; асимметрия распределения тем больше, чем больше разница между вероятностями p и q.
Распределение Пуассона
Распределение Пуассона является частным случаем биномиального распределения, используемым при очень низкой вероятности интересующих нас событий. Другими словами, это распределение описывает вероятность редких событий. Формулой Пуассона можно пользоваться при p < 0,01 и q ≥ 0,99.
Уравнение Пуассона является приближенным и описывается следующей формулой:
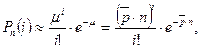(6.9)
где μ представляет собой произведение средней вероятности события и числа наблюдений.
В качестве примера рассмотрим алгоритм решения следующей задачи.
Условие задачи
За несколько лет в 21 крупной клинике России было проведено массовое обследование новорожденных на предмет заболевания младенцев болезнью Дауна (выборка в среднем составляла 1000 новорожденных в каждой клинике). Были получены следующие данные:
| Число клиник | 11 | 6 | 2 | 1 | 1 | 0 |
| Число заболеваний | 0 | 1 | 2 | 3 | 4 | 5 |
Задание
1. Определить среднюю вероятность заболевания (в пересчете на число новорожденных).
2. Определить, на какое число новорожденных в среднем приходится одно заболевание.
3. Определить вероятность того, что среди 100 случайно выбранных новорожденных обнаружится 2 младенца с болезнью Дауна.
Решение
1. Определяем среднюю вероятность заболевания. При этом мы должны руководствоваться следующими рассуждениями. Болезнь Дауна зарегистрирована лишь в 10 клиниках из 21. В 11 клиниках заболеваний не обнаружено, в 6 клиниках зарегистрировано по 1 случаю, в 2 клиниках – 2 случая, в 1-й клинике – 3 и в 1-й клинике – 4 случая болезни. 5 случаев заболевания не было обнаружено ни в одной клинике. Для того чтобы определить среднюю вероятность заболевания, необходимо общее число случаев (6·1 + 2·2 + 1·3 + 1·4 = 17) разделить на общее число новорожденных (21000):
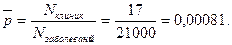
2. Число новорожденных, на которое приходится одно заболевание, является величиной обратной средней вероятности, т. е. равно общему числу новорожденных, отнесенному к числу зарегистрированных случаев:
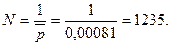
3. Подставляем значения p = 0,00081, n = 100 и i = 2 в формулу Пуассона:
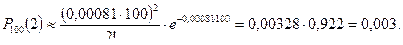
Ответ
Вероятность того, что среди 100 случайно выбранных новорожденных обнаружится 2 младенца с болезнью Дауна, составляет 0,003 (0,3%).
Задачи по теме
Задача 6. 1
Задание
Пользуясь данными задачи 5.1 по времени сенсомоторной реакции, вычислить асимметрию и эксцесс распределения ВР.
Задача 6. 2
200 учащихся выпускных классов были протестированы на уровень интеллектуальности (IQ). После нормирования полученного распределения IQ по стандартному отклонению были получены следующие результаты:
| Классовый интервал | Частоты IQ | Классовый интервал | Частоты IQ |
| – 4,0 ¸ – 3,5 s | 0 | 0 ¸ 0,5 s | 31 |
| – 3,5 ¸ – 3,0 s | 2 | 0,5 ¸ 1,0 s | 14 |
| – 3,0 ¸ – 2,5 s | 6 | 1,0 ¸ 1,5 s | 4 |
| – 2,5 ¸ – 2,0 s | 12 | 1,5 ¸ 2,0 s | 2 |
| – 2,0 ¸ – 1,5 s | 18 | 2,0 ¸ 2,5 s | 1 |
| – 1,5 ¸ – 1,0 s | 28 | 2,5 ¸ 3,0 s | 1 |
| – 1,0 ¸ – 0,5 s | 39 | 3,0 ¸ 3,5 s | 0 |
| – 0,5 s ¸ 0 | 42 | 3,5 ¸ 4,0 s | 0 |
Задание
Пользуясь критериями Колмогорова и хи-квадрат, определить, соответствует ли полученное распределение показателей IQ нормальному.
Задача 6. 3
У взрослого испытуемого (мужчина 25 лет) исследовалось время простой сенсомоторной реакции (ВР) в ответ на звуковой стимул с постоянной частотой в 1 кГц и интенсивностью 40 дБ. Стимул предъявлялся стократно с интервалами 3 – 5 секунд. Отдельные значения ВР по 100 повторностям распределилось следующим образом:
| Время реакции, мс | 100¸110 | 110¸120 | 120¸130 | 130¸140 | 140¸150 | 150¸160 | 160¸170 | 170¸180 |
| Число испытуемых | 9 | 15 | 28 | 30 | 8 | 5 | 3 | 2 |
Задание
1. Построить частотную гистограмму распределения ВР; определить среднее значение ВР и величину стандартного отклонения.
2. Рассчитать коэффициент асимметрии и показатель эксцесса распределения ВР; на основании полученных значений As и Ex сделать вывод о соответствии или несоответствии данного распределения нормальному.
Задача 6. 4
В 1998 году в Нижнем Тагиле окончили школы с золотыми медалями 14 человек (5 юношей и 9 девушек), с серебряными – 26 человек (8 юношей и 18 девушек).
Вопрос
Можно ли утверждать, что девушки получают медали чаще, чем юноши?
Примечание
Соотношение числа юношей и девушек в генеральной совокупности считать равным.
Задача 6. 5
Считается, что число экстравертов и интровертов в однородной группе испытуемых является приблизительно одинаковым.
Задание
Определить вероятность того, что в группе из 10 случайно отобранных испытуемых обнаружится 0, 1, 2, ..., 10 экстравертов. Построить графическое выражение распределения вероятностей обнаружения 0, 1, 2, ..., 10 экстравертов в данной группе.
Задача 6. 6
Задание
Рассчитать вероятность P n(i) функции биномиального распределения при p = 0,3 и q = 0,7 для значений n = 5 и i = 0, 1, 2, ..., 5. Построить графическое выражение зависимости P n(i) = f (i).
Задача 6. 7
В последние годы среди определенной части населения утвердилась вера в астрологические прогнозы. По результатам предварительных опросов установлено, что в астрологию верят около 15% населения.
Задание
Определить вероятность того, что среди 10 случайно выбранных респондентов окажется 1, 2 или 3 человека, верящих в астрологические прогнозы.
Задача 6. 8
Условие задачи
В 42 общеобразовательных школах г. Екатеринбурга и Свердловской области (общее число учащихся 12260 человек) за несколько лет было выявлено следующее число случаев психических заболеваний среди школьников:
| Число школ (n) | 22 | 13 | 4 | 2 | 1 | 0 |
| Число случаев (i) | 0 | 1 | 2 | 3 | 4 | 5 |
Задание
Пусть будет выборочно обследовано 1000 школьников. Рассчитать, какова вероятность того, что среди этой тысячи школьников будет выявлен 1, 2 или 3 психически больных ребенка?
РАЗДЕЛ 7. МЕРЫ РАЗЛИЧИЙ
Постановка проблемы
Предположим, что мы имеем две независимые друг от друга выборки испытуемых х и у. Независимыми выборки считаются тогда, когда один и тот же субъект (испытуемый) фигурирует только в одной выборке. Задача состоит в том, чтобы сравнить между собой эти выборки (два ряда переменных) на предмет их различий. Естественно, что как бы ни были близки между собой значения переменных в первой и второй выборке, какие-то, пусть даже незначительные, различия между ними будут обнаруживаться. С точки же зрения математической статистики нас интересует вопрос, являются ли различия между этими выборками статистически достоверными (статистически значимыми) или недостоверными (случайными).
Наиболее распространенными критериями достоверности различий между выборками являются параметрические меры различий – критерий Стьюдента и критерий Фишера. В ряде случаев используются непараметрические критерии – критерий Q Розенбаума, U-критерий Манна- Уитни и др. Особое место занимает угловое преобразование Фишера φ*, позволяющие сравнивать друг с другом значения, выраженные в процентах (процентных долях). И, наконец, как частный случай, для сравнения выборок могут быть использованы критерии, характеризующие форму распределений выборок – критерий χ2 Пирсона и критерий λ Колмогорова – Смирнова.
В целях наилучшего усвоения данной темы мы поступим следующим образом. Одну и ту же задачу мы решим четырьмя методами с использованием четырех различных критериев – Розенбаума, Манна-Уитни, Стьюдента и Фишера.
Условие задачи
30 студентов (14 юношей и 16 девушек) во время экзаменационной сессии протестированы по тесту Спилбергера на уровень реактивной тревожности. Получены следующие результаты (табл. 7.1):
Таблица 7.1
| Испытуемые | Уровень реактивной тревожности | |||||||||||||||
| Юноши | 32 | 34 | 28 | 43 | 35 | 26 | 41 | 32 | 40 | 39 | 42 | 38 | 44 | 33 | ||
| Девушки | 34 | 30 | 37 | 43 | 42 | 44 | 46 | 36 | 45 | 28 | 34 | 41 | 40 | 35 | 42 | 39 |
Задание
Определить, являются ли статистически достоверными различия уровня реактивной тревожности у юношей и девушек.
Задача представляется вполне типичной для психолога, специализирующегося в области педагогической психологии: кто более остро переживает экзаменационный стресс – юноши или девушки? Если различия между выборками статистически достоверны, то существуют значимые половые различия в данном аспекте; если различия случайны (статистически недостоверны), от данного предположения следует отказаться.
7. 2. Непараметрический критерий Q Розенбаума
Q-критерий Розенбаума основан на сравнении «наложенных» друг на друга ранжированных рядов значений двух независимых переменных. При этом не анализируется характер распределения признака внутри каждого ряда – в данном случае имеет значение лишь ширина неперекрывающихся участков двух ранжированных рядов. При сравнении между собой двух ранжированных рядов переменных возможны 3 варианта:
1. Ранжированные ряды x и y не имеют области перекрытия, т. е. все значения первого ранжированного ряда (x) больше всех значений второго ранжированного ряда (y):
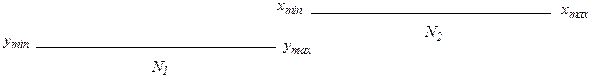
В данном случае различия между выборками, определяемые по любому статистическому критерию, безусловно достоверны, и использование критерия Розенбаума не требуется. Тем не менее на практике такой вариант встречается исключительно редко.
2. Ранжированные ряды полностью накладываются друг на друга (как правило, один из рядов находится внутри другого), неперекрывающиеся зоны отсутствуют. В данном случае критерий Розенбаума неприменим.
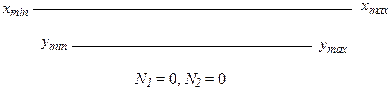
3. Имеется зона перекрытия рядов, а также две неперекрывающиеся области (N 1 и N 2), относящиеся к разным ранжированным рядам (обозначим х – ряд, сдвинутый в сторону больших, y – в сторону меньших значений):
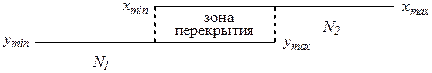
Данный случай является типичным для использования критерия Розенбаума, при использовании которого следует соблюдать следующие условия:
1. Объем каждой выборки должен быть не менее 11.
2. Объемы выборок не должны существенно отличаться друг от друга.
Критерий Q Розенбаума соответствует числу неперекрывающихся значений: Q = N1 + N2. Вывод о достоверности различий между выборками делается в случае, если Q > Qкр. При этом значения Qкр находятся в специальных таблицах (см. Приложение, табл. VIII).
Вернемся к нашей задаче. Введем обозначения: х – выборка девушек, y – выборка юношей. Для каждой выборки строим ранжированный ряд:
х: 28 30 34 34 35 36 37 39 40 41 42 42 43 44 45 46
y: 26 28 32 32 33 34 35 38 39 40 41 42 43 44
Подсчитываем число значений в неперекрывающихся областях ранжированных рядов. В ряду х неперекрывающимися являются значения 45 и 46, т. е. N1 = 2; в ряду y только 1 неперекрывающееся значение 26, т. е. N2 = 1. Отсюда, Q = N1 + N2 = 1 + 2 = 3.
В табл. VIII Приложения находим, что Qкр.= 7 (для уровня значимости 0,95) и Qкр = 9 (для уровня значимости 0,99).
Вывод
Поскольку Q < Qкр, то по критерию Розенбаума различия между выборками не являются статистически достоверными.
Примечание
Критерий Розенбаума может использоваться независимо от характера распределения переменных, т. е. в данном случае отпадает необходимость использования критериев χ2 Пирсона и λ Колмогорова для определения типа распределений в обеих выборках.
7. 3. U-критерий Манна – Уитни
В отличие от критерия Розенбаума, U-критерий Манна – Уитни основан на определении зоны перекрытия между двумя ранжированными рядами, т. е. чем меньше зона перекрытия, тем достовернее различия между выборками. Для этого используется специальная процедура преобразования интервальных шкал в ранговые.
Рассмотрим алгоритм вычислений по U-критерию на примере предыдущей задачи.
Для более экономичной работы рекомендуется построение рабочей таблицы следующего вида (табл. 7.2).
Таблица 7.2
| x, y | Rxy | Rxy* | Rx | Ry |
| 1 | 2 | 3 | 4 | 5 |
| 26 28 28 30 32 32 33 34 34 34 35 35 36 37 38 39 39 40 40 41 41 42 42 42 43 43 44 44 45 46 | 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 | 1 2,5 2,5 4 5,5 5,5 7 9 9 9 11,5 11,5 13 14 15 16,5 16,5 18,5 18,5 20,5 20,5 23 23 23 25,5 25,5 27,5 27,5 29 30 | 2,5 4 9 9 11,5 13 14 16,5 18,5 20,5 23 23 25,5 27,5 29 30 | 1 2,5 5,5 5,5 7 9 11,5 15 16,5 18,5 20,5 23 25,5 27,5 |
| Σ | 276,5 | 188,5 |
Рекомендуется следующий порядок заполнения таблицы и соответствующих вычислений:
1. Из двух независимых выборок строим единый ранжированный ряд. В данном случае значения для обеих выборок идут «вперемешку», столбец 1 (x, y). В целях упрощения дальнейшей работы (в том числе и в компьютерном варианте) следует значения для разных выборок отмечать разным шрифтом (или разным цветом) с учетом того, что в дальнейшем мы будем их разносить по разным столбцам.
2. Преобразуем интервальную шкалу значений в порядковую (для этого переобозначаем все значения ранговыми числами от 1 до 30, столбец 2 (Rxy)).
3. Вводим поправки на связанные ранги (одинаковые значения переменной обозначаются одним и тем же рангом при условии, что сумма рангов не изменяется, столбец 3 (Rxy*). На этом этапе рекомендуется подсчитать суммы рангов во 2-м и 3-м столбце (если все поправки введены верно, то эти суммы должны быть равны).
4. Разносим ранговые числа в соответствии с их принадлежностью к той или иной выборке (столбцы 4 и 5 (Rx и Ry)).
5. Проводим вычисления по формуле:
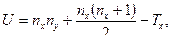(7.1)
где Тх – наибольшая из ранговых сумм; nx и ny, соответственно, объемы выборок. В данном случае следует иметь в виду, что если Tx < Ty, то обозначения x и y следует сменить на обратные.
6. Сравниваем полученное значение с табличным (см. Приложения, табл. IX). Вывод о достоверности различий между двумя выборками делается в случае, если Uэксп. < Uкр..
В нашем примере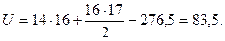 
Uэксп. = 83,5 > U кр. = 71.
Вывод
Различия между двумя выборками по критерию Манна – Уитни не являются статистически достоверными.
Примечания
1. Критерий Манна-Уитни не имеет практически никаких ограничений; минимальные объемы сравниваемых выборок – 2 и 5 человек (см. табл. IX Приложения).
2. Аналогично критерию Розенбаума критерий Манна-Уитни может быть использован применительно к любым выборкам независимо от характера распределения.
Критерий Стьюдента
В отличие от критериев Розенбаума и Манна-Уитни критерий t Стьюдента является параметрическим, т. е. основан на определении основных статистических показателей – средних значений в каждой выборке (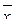 
и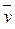 
) и их дисперсий (s2x и s2y), рассчитываемых по стандартным формулам (см. раздел 5).
Использование критерия Стьюдента предполагает соблюдение следующих условий:
1. Распределения значений для обеих выборок должны соответствовать закону нормального распределения (см. раздел 6).
2. Суммарный объем выборок должен быть не менее 30 (для β1 = 0,95) и не менее 100 (для β2 = 0,99).
3. Объемы двух выборок не должны существенно отличаться друг от друга (не более чем в 1,5 ÷ 2 раза).
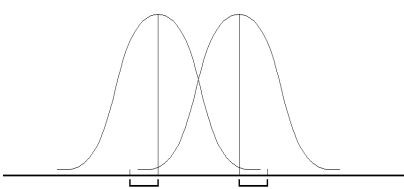
Идея критерия Стьюдента достаточно проста. Предположим, что значения переменных в каждой из выборок распределяются по нормальному закону, т. е. мы имеем дело с двумя нормальными распределениями, отличающимися друг от друга по средним значениям и дисперсии (соответственно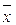 
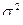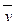и 
, 
и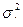 
, см. рис. 7.1).
sx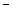 
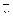sy
Рис. 7.1. Оценка различий между двумя независимыми выборкам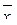и: 
и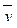 
- средние значения выборок x и y; sx и sy - стандартные отклонения
Нетрудно понять, что различия между двумя выборками будут тем больше, чем больше разность между средними значениями и чем меньше их дисперсии (или стандартные отклонения).
В случае независимых выборок коэффициент Стьюдента определяют по формуле:
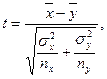(7.2)
где nx и ny – соответственно численность выборок x и y.
После вычисления коэффициента Стьюдента в таблице стандартных (критических) значений t (см. Приложение, табл. Х) находят величину, соответствующую числу степеней свободы n = nx + ny – 2, и сравнивают ее с рассчитанной по формуле. Если tэксп. £ tкр., то гипотезу о достоверности различий между выборками отвергают, если же tэксп. > tкр., то ее принимают. Другими словами, выборки достоверно отличаются друг от друга, если вычисленный по формуле коэффициент Стьюдента больше табличного значения для соответствующего уровня значимости.
В рассмотренной нами ранее задаче вычисление средних значений и дисперсий дает следующие значения: xср. = 38,5; σх2 = 28,40; уср. = 36,2; σу2 = 31,72.
Можно видеть, что среднее значение тревожности в группе девушек выше, чем в группе юношей. Тем не менее эти различия настолько незначительны, что вряд ли они являются статистически значимыми. Разброс значений у юношей, напротив, несколько выше, чем у девушек, но различия между дисперсиями также невелики.
Подставляем значения в формулу: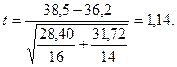 
Вывод
tэксп. = 1,14 < tкр. = 2,05 (β1 = 0,95). Различия между двумя сравниваемыми выборками не являются статистически достоверными. Данный вывод вполне согласуется с таковым, полученным при использовании критериев Розенбаума и Манна-Уитни.
Другой способ определения различий между двумя выборками по критерию Стьюдента состоит в вычислении доверительного интервала стандартных отклонений. Доверительным интервалом называется среднеквадратичное (стандартное) отклонение, деленное на корень квадратный из объема выборки и умноженное на стандартное значение коэффициента Стьюдента для n – 1 степеней свободы (соответственно, 
и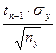 
).
Примечание
Величина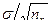 
= mx называется среднеквадратичной ошибкой (см. раздел 5). Следовательно, доверительный интервал есть среднеквадратичная ошибка, умноженная на коэффициент Стьюдента для данного объема выборки, где число степеней свободы ν = n – 1, и заданного уровня значимости.
Две независимые друг от друга выборки считаются достоверно различающимися, если доверительные интервалы для этих выборок не перекрываются друг с другом. В нашем случае мы имеем для первой выборки 38,5 ± 2,84, для второй 36,2 ± 3,38.
Следовательно, случайные вариации xi лежат в диапазоне 35,66 ¸ 41,34, а вариации yi – в диапазоне 32,82 ¸ 39,58. На основании этого можно констатировать, что различия между выборками x и y статистически недостоверны (диапазоны вариаций перекрываются друг с другом). При этом следует иметь в виду, что ширина зоны перекрытия в данном случае не имеет значения (важен лишь сам факт перекрытия доверительных интервалов).
Метод Стьюдента для зависимых друг от друга выборок (например, для сравнения результатов, полученных при повторном тестировании на одной и той же выборке испытуемых) используют достаточно редко, поскольку для этих целей существуют другие, более информативные статистические приемы (см. раздел 10). Тем не менее, для данной цели в первом приближении можно использовать формулу Стьюдента следующего вида:
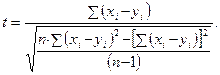(7.3)
Полученный результат сравнивают с табличным значением для n – 1 степеней свободы, где n – число пар значений x и y. Результаты сравнения интерпретируются точно так же, как и в случае вычисления различий между двумя независимыми выборками.
Критерий Фишера
Критерий Фишера (F) основан на том же принципе, что и критерий Стьюдента, т. е. предполагает вычисление средних значений и дисперсий в сравниваемых выборках. Чаще всего используется при сравнении между собой неравноценных по объему (разных по численности) выборок. Критерий Фишера является несколько более жестким, чем критерий Стьюдента, а потому более предпочтителен в тех случаях, когда возникают сомнения в достоверности различий (например, если по критерию Стьюдента различия достоверны при нулевом и недостоверны при первом уровне значимости).
Формула Фишера выглядит следующим образом:
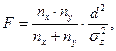(7.4)
где 
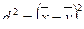и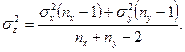 
(7.5, 7.6)
В рассматриваемой нами задаче d 2 = 5,29; σz2 = 29,94.
Подставляем значения в формулу: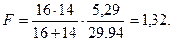 
В табл. ХI Приложений находим, что для уровня значимости β1 = 0,95 и ν = nx + ny – 2 = 28 критическое значение составляет 4,20.
Вывод
F = 1,32 < F кр. = 4,20. Различия между выборками статистически недостоверны.
Примечание
При использовании критерия Фишера должны соблюдаться те же условия, что и для критерия Стьюдента (см. подраздел 7.4). Тем не менее допускается различие в численности выборок более чем в два раза.
Таким образом, при решении одной и той же задачи четырьмя различными методами с использованием двух непараметрических и двух параметрических критериев мы пришли к однозначному выводу о том, что различия между группой девушек и группой юношей по уровню реактивной тревожности недостоверны (т. е. находятся в пределах случайных вариаций). Однако могут встретиться и такие случаи, когда сделать однозначный вывод не представляется возможным: одни критерии дают достоверные, другие – недостоверные различия. В этих случаях приоритет отдается параметрическим критериям (при условии достаточности объема выборок и нормального распределения исследуемых величин).
7. 6. Критерий j* - угловое преобразование Фишера
Критерий j* Фишера предназначен для сопоставления двух выборок по частоте встречаемости интересующего исследователя эффекта. Он оценивает достоверность различий между процентными долями двух выборок, в которых зарегистрирован интересующий нас эффект. Допускается также сравнение процентных соотношений и в пределах одной выборки.
Суть углового преобразования Фишера состоит в переводе процентных долей в величины центрального угла, который измеряется в радианах. Большей процентной доле будет соответствовать больший угол j, а меньшей доле – меньший угол, но отношения здесь нелинейные:
(7.7)
где Р – процентная доля, выраженная в долях единицы.
При увеличении расхождения между углами j1 и j2 и увеличении численности выборок значение критерия возрастает.
Критерий Фишера вычисляется по следующей формуле:
(7.8)
где j1 – угол, соответствующий большей процентной доле; j2 – угол, соответствующий меньшей процентной доле; n1 и n2 – соответственно, объем первой и второй выборок.
Вычисленное по формуле значение сравнивается со стандартным (j*ст = 1,64 для b1 = 0,95 и j*ст = 2,31 для b2 = 0,99. Различия между двумя выборками считаются статистически достоверными, если j* > j*ст для данного уровня значимости.
Пример
Нас интересует, различаются ли между собой две группы студентов по успешности выполнения достаточно сложной задачи. В первой группе из 20 человек с ней справилось 12 студентов, во второй – 10 человек из 25.
Решение
1. Вводим обозначения: n1 = 20, n2 = 25.
2. Вычисляем процентные доли Р1 и Р2: Р1 = 12 / 20 = 0,6 (60%), Р2 = 10 / 25 = 0,4 (40%).
3. В табл. XII Приложений находим соответствующие процентным долям значения φ: j1 = 1,772, j2 = 1,369.
 |
Отсюда:
Вывод
Различия между группами не являются статистически достоверными, поскольку j* < j*ст для 1-го и тем более для 2-го уровня значимости.
7.7. Использование критерия χ2 Пирсона и критерия λ Колмогорова
Дата: 2018-11-18, просмотров: 561.
