Среднее арифметическое значение, или просто среднее ( 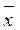 ), равно сумме переменных, деленной на их число.
), равно сумме переменных, деленной на их число.
Для несгруппированных переменных среднее арифметическое вычисляется по формуле:
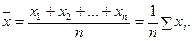 (4.1)
(4.1)
Для сгруппированных переменных можно воспользоваться другой формулой – среднее будет соответствовать сумме произведений средних значений каждого класса и частоты встречаемости значения признака в данном классе:
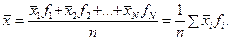 (4.2)
(4.2)
Среднее арифметическое может использоваться и для тех признаков, для которых не найден способ количественного измерения (шкала порядка). Для этого в качестве xi используются ранговые числа, а среднее принято называть непараметрическим средним.
Взвешенное среднее арифметическое используется в тех случаях, когда разные составляющие имеют разный «удельный вес» в формировании общей совокупности:
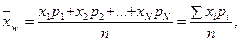 (4.3)
(4.3)
или: 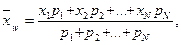 (4.4)
(4.4)
где n – объем выборки, N – число классов.
Пример
Средний балл аттестата учащихся выпускных классов одной из школ соответствует следующим значениям: 11-а – 4,2; 11-б – 4,0 и 11-в – 3,8. Численность этих классов составляет: 11-а – 25 человек, 11-б – 28 и 11-в – 32 человека. В данном случае средний балл аттестата по всем выпускным классам составит (4,2 × 25 + 4,0 × 28 + 3,8 × 32) : (25 + 28 + 32) = 3,98.
Среднее принято округлять с точностью до знака, следующего за последним знаком xi (увеличение точности на порядок).
Свойства среднего
1. Сумма всех отклонений от среднего значения равна нулю: 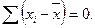
Доказательство:
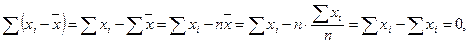 поскольку `
поскольку ` 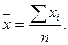
2. Если константу с прибавить к каждому значению, то среднее 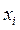 превратится в
превратится в 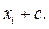
Доказательство:
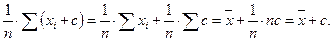
3. Если каждое значение множества со средним 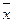 умножить на константу c, то среднее станет равным
умножить на константу c, то среднее станет равным 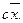
Доказательство: 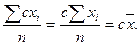
4. Сумма квадратов отклонений значений от их среднего арифметического меньше суммы квадратов отклонений от любой другой точки: 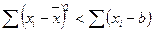 (при условии, что b ¹ ` x ).
(при условии, что b ¹ ` x ).
Доказательство: 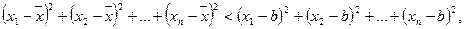 где
где 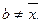
Примем 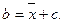 Тогда:
Тогда:
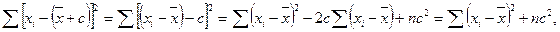
поскольку 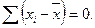
Так как c2 > 0, то: 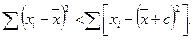
4. 4. Среднее геометрическое значение
Среднее геометрическое значение (xg) используется для вычисления центральной тенденции при прогрессивно возрастающих квантилях (когда распределение значений переменной имеет выраженную положительную (правостороннюю) асимметрию).
Формула среднего геометрического:
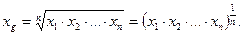 (4.5)
(4.5)
Для вычислений можно использовать логарифмирование каждой переменной по основанию е:
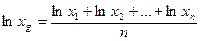 (4.6)
(4.6)
Переход от ln xg к xg осуществляется с помощью операции антилогарифмирования:
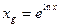 (4.7)
(4.7)
Задачи по теме
Задача 4.1
Условие задачи
У 50 школьников выпускных классов исследовался коэффициент интеллекта (IQ). Получен следующий вариационный ряд (см. табл.).
| №№ | IQ | №№ | IQ | №№ | IQ | №№ | IQ | №№ | IQ | ||||||||
| 1 | 119 | 11 | 104 | 21 | 111 | 31 | 103 | 41 | 107 | ||||||||
| 2 | 86 | 12 | 88 | 22 | 98 | 32 | 88 | 42 | 92 | ||||||||
| 3 | 100 | 13 | 113 | 23 | 84 | 33 | 108 | 43 | 105 | ||||||||
| 4 | 93 | 14 | 89 | 24 | 102 | 34 | 70 | 44 | 89 | ||||||||
| 5 | 108 | 15 | 103 | 25 | 92 | 35 | 113 | 45 | 95 | ||||||||
| 6 | 117 | 16 | 107 | 26 | 88 | 36 | 83 | 46 | 110 | ||||||||
| 7 | 82 | 17 | 78 | 27 | 104 | 37 | 91 | 47 | 101 | ||||||||
| 8 | 100 | 18 | 110 | 28 | 127 | 38 | 97 | 48 | 85 | ||||||||
| 9 | 86 | 19 | 98 | 29 | 103 | 39 | 87 | 49 | 114 | ||||||||
| 10 | 129 | 20 | 84 | 30 | 112 | 40 | 101 | 50 | 102 | ||||||||
Задание
1. Построить ранжированный ряд IQ.
2. Построить таблицу сгруппированных частот для 7 ¸ 8-классового распределения.
3. Построить графическое выражение IQ в виде полигона распределения или столбчатой диаграммы.
4. Определить 1-й, 2-й и 3-й квартили, моду, медиану и среднее арифметическое значение коэффициента интеллектуальности для выборки в 50 испытуемых.
Задача 4.2
Условие задачи
В трех выпускных классах средней школы подсчитывался средний балл успеваемости. Получены следующие результаты:
| 11-а класс | 11-б класс | 11-в класс | ||||||
| Пол | Число учащихся | Балл | Число учащихся | Балл | Число учащихся | Балл | ||
| Девочки | 18 | 3,62 | 15 | 3,90 | 17 | 3,75 | ||
| Мальчики | 12 | 3,44 | 13 | 3,58 | 13 | 3,70 | ||
Задание
Вычислить средний балл успеваемости у девочек и мальчиков всех выпускных классов.
Задача 4. 3
Имеется следующая совокупность экспериментальных данных: 1,00; 1,26; 1,58; 2,00; 2,51; 3,16; 3,98; 5,01; 6,31; 7,94.
Задание
Вычислить среднее геометрическое значение данной совокупности двумя способами:
а) вычислением произведения значений и возведения в соответствующую степень;
б) путем логарифмирования по основанию e.
РАЗДЕЛ 5.
МЕРЫ ИЗМЕНЧИВОСТИ (РАЗНООБРАЗИЯ, ВАРИАТИВНОСТИ) исследуемого ПРИЗНАКА
Две выборочные совокупности могут иметь одинаковые или близкие между собой средние значения признака и в то же время существенно различаться по степени вариабельности (вариативности) этого признака.
Например, имеется две группы испытуемых (по 100 человек в каждой), у которых исследуется коэффициент интеллекта (IQ). Средние значения IQ в той и другой группе могут приблизительно совпадать (допустим, IQ1 = 102 и IQ2 = 97), и констатация этого факта даст нам очень немного информации. В то же время известно, что индивидуальные значения в первой группе испытуемых изменяются от 85 до 116, а во второй от 60 до 135. На основании этого мы можем сказать, что вторая выборка обладает большим разнообразием признака по сравнению с первой.
Для определения степени разнообразия (изменчивости) исследуемого параметра используются различные критерии: пределы разнообразия, размах вариаций, среднее и стандартное отклонения, дисперсия, коэффициент вариации и др.
Дата: 2018-11-18, просмотров: 786.