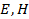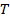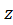Между обкладками конденсатора существует электрическое поле (ЭП), энергия которого 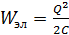 . В катушке, по которой протекает ток
. В катушке, по которой протекает ток 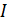 , создается магнитное поле (МП) с энергией
, создается магнитное поле (МП) с энергией 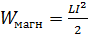 . Полная энергия колебательного контура равна сумме этих энергий:
. Полная энергия колебательного контура равна сумме этих энергий:
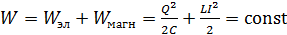 . (8)
. (8)
Полная энергия колебаний остается постоянной, так как тепловые потери энергии при протекании тока отсутствуют: 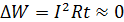 , благодаря тому, что активное сопротивление контура
, благодаря тому, что активное сопротивление контура 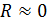 . Но в контуре при колебаниях происходят взаимные превращения энергии электрического и магнитного полей. Графики изменения со временем колеблющихся величин в ИКК представлены на рис. 2.
. Но в контуре при колебаниях происходят взаимные превращения энергии электрического и магнитного полей. Графики изменения со временем колеблющихся величин в ИКК представлены на рис. 2.
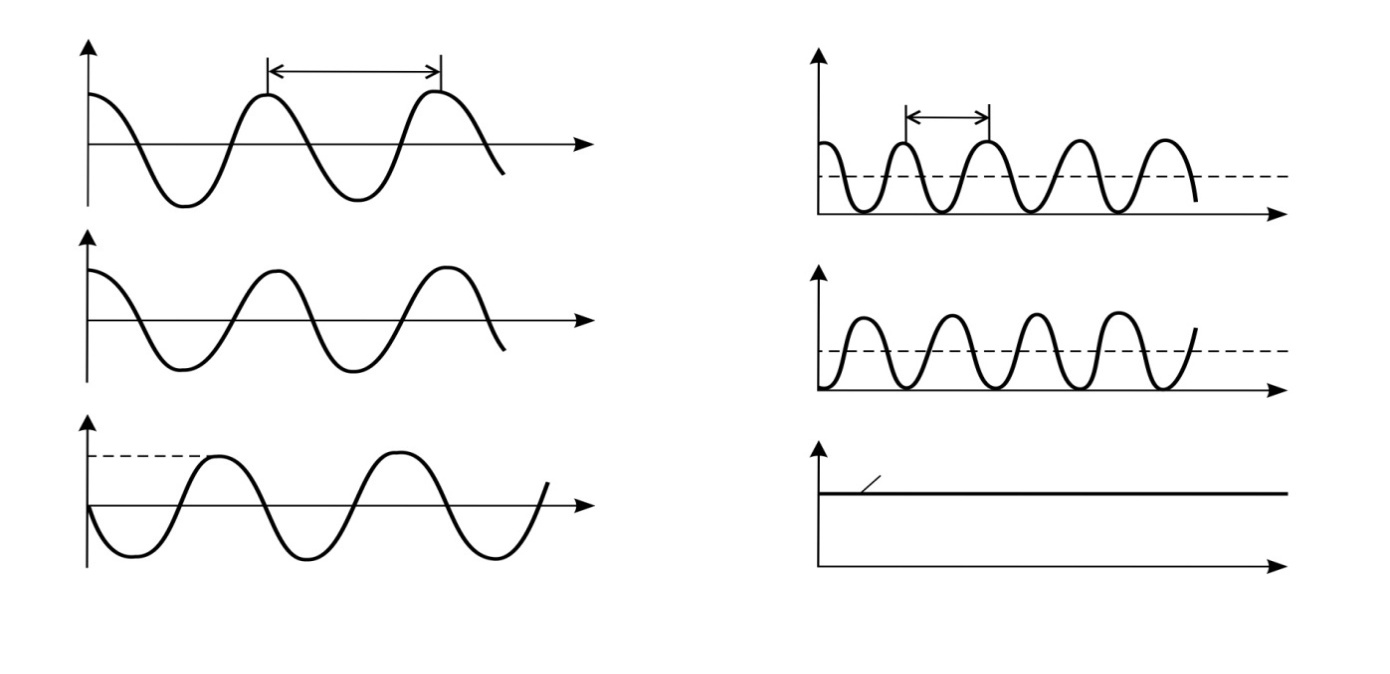
Рис. 2
|
|
1.4. Волновые процессы. Параметры и уравнение бегущей волны
Волновой процесс, или волна – процесс распространения колебаний некоторой величины 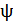 . Электромагнитная волна (ЭМВ) – распространение в пространстве переменного электромагнитного поля. Волна называется гармонической, если колебания характеристик полей: напряженности ЭП
. Электромагнитная волна (ЭМВ) – распространение в пространстве переменного электромагнитного поля. Волна называется гармонической, если колебания характеристик полей: напряженности ЭП 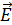 и напряженности МП
и напряженности МП 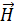 являются гармоническими. В ЭМВ колеблющаяся величина
являются гармоническими. В ЭМВ колеблющаяся величина 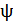 – это
– это 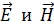 .
.
В гармонической волне функция 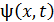 является 1) периодической во времени, т. е. в каждой точке пространства колебания величины
является 1) периодической во времени, т. е. в каждой точке пространства колебания величины 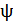 происходят по гармоническому закону с периодом
происходят по гармоническому закону с периодом 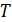 (рис. 3а), и 2) периодической в пространстве – фаза колебаний повторяется в пространстве с периодом
(рис. 3а), и 2) периодической в пространстве – фаза колебаний повторяется в пространстве с периодом 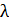 , называемым длиной волны (рис. 3б).
, называемым длиной волны (рис. 3б).
Длина волны 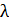 равна расстоянию, которое проходит волна за период колебаний:
равна расстоянию, которое проходит волна за период колебаний:
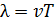 ,
,
где период 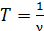 ; в результате
; в результате
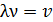 . (9)
. (9)
Здесь 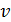 – фазовая скорость волны (скорость переноса фазы колебаний);
– фазовая скорость волны (скорость переноса фазы колебаний); 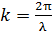 – волновое число.
– волновое число.
Бегущей называют такую волну, которая (в отличие от стоячей волны) переносит в пространстве энергию. По форме фронта волна может быть плоской или сферической; для этих волн фронт волны, соответственно, плоскость и сфера.
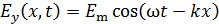 ;
;
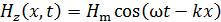 . (10)
. (10)
Здесь 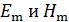 – амплитуды напряженностей электрического и магнитного полей ЭМВ;
– амплитуды напряженностей электрического и магнитного полей ЭМВ; 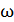 – циклическая частота волны;
– циклическая частота волны; 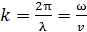 – волновое число;
– волновое число; 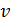 – фазовая скорость волны;
– фазовая скорость волны; 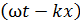 – фаза плоской волны.
– фаза плоской волны.
Уравнения волны (10) выявляют следующие свойства ЭМВ. Эта волна является
поперечной: колеблющиеся векторы
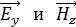
перпендикулярны направлению распространения волны – оси
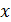
и скорости волны
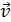
. Напряженности полей
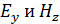
колеблются в одинаковой фазе, при этом их максимумы
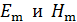
достигаются одновременно и в одной и той же точке пространства; также и нули (
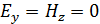
) достигаются одновременно. Мгновенная (в данный момент времени
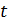
) картина полей в ЭМВ, бегущей вдоль оси
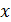
, показана на рис. 4.
При распространении ЭМВ в среде скорость волны 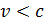 , зависит от свойств среды и определяется следующей формулой:
, зависит от свойств среды и определяется следующей формулой:
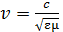 ,
,
где 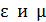 – диэлектрическая и магнитная проницаемости среды.
– диэлектрическая и магнитная проницаемости среды.
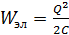 . В катушке, по которой протекает ток
. В катушке, по которой протекает ток 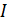 , создается магнитное поле (МП) с энергией
, создается магнитное поле (МП) с энергией 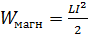 . Полная энергия колебательного контура равна сумме этих энергий:
. Полная энергия колебательного контура равна сумме этих энергий: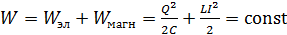 . (8)
. (8)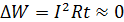 , благодаря тому, что активное сопротивление контура
, благодаря тому, что активное сопротивление контура 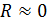 . Но в контуре при колебаниях происходят взаимные превращения энергии электрического и магнитного полей. Графики изменения со временем колеблющихся величин в ИКК представлены на рис. 2.
. Но в контуре при колебаниях происходят взаимные превращения энергии электрического и магнитного полей. Графики изменения со временем колеблющихся величин в ИКК представлены на рис. 2.
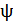 . Электромагнитная волна (ЭМВ) – распространение в пространстве переменного электромагнитного поля. Волна называется гармонической, если колебания характеристик полей: напряженности ЭП
. Электромагнитная волна (ЭМВ) – распространение в пространстве переменного электромагнитного поля. Волна называется гармонической, если колебания характеристик полей: напряженности ЭП 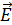 и напряженности МП
и напряженности МП 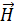 являются гармоническими. В ЭМВ колеблющаяся величина
являются гармоническими. В ЭМВ колеблющаяся величина 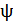 – это
– это 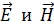 .
.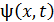 является 1) периодической во времени, т. е. в каждой точке пространства колебания величины
является 1) периодической во времени, т. е. в каждой точке пространства колебания величины 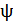 происходят по гармоническому закону с периодом
происходят по гармоническому закону с периодом 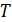 (рис. 3а), и 2) периодической в пространстве – фаза колебаний повторяется в пространстве с периодом
(рис. 3а), и 2) периодической в пространстве – фаза колебаний повторяется в пространстве с периодом 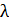 , называемым длиной волны (рис. 3б).
, называемым длиной волны (рис. 3б).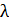 равна расстоянию, которое проходит волна за период колебаний:
равна расстоянию, которое проходит волна за период колебаний: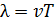 ,
,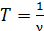 ; в результате
; в результате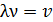 . (9)
. (9)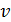 – фазовая скорость волны (скорость переноса фазы колебаний);
– фазовая скорость волны (скорость переноса фазы колебаний); 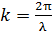 – волновое число.
– волновое число.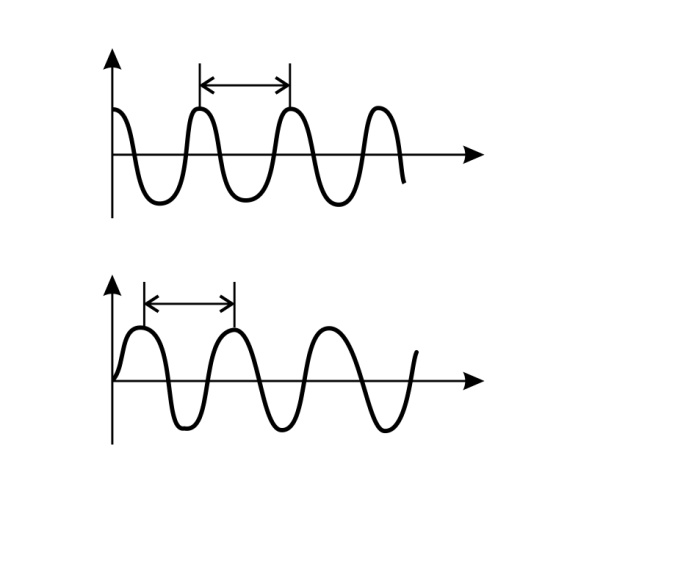
 , которая дает закон колебаний
, которая дает закон колебаний 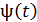 в любой точке пространства с координатами
в любой точке пространства с координатами 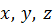 . Уравнение плоской гармонической электромагнитной волны, бегущей вдоль оси
. Уравнение плоской гармонической электромагнитной волны, бегущей вдоль оси 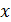 – это функция
– это функция 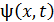 , которая имеет следующий вид:
, которая имеет следующий вид:
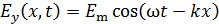 ;
;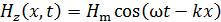 . (10)
. (10)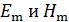 – амплитуды напряженностей электрического и магнитного полей ЭМВ;
– амплитуды напряженностей электрического и магнитного полей ЭМВ; 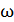 – циклическая частота волны;
– циклическая частота волны; 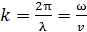 – волновое число;
– волновое число; 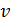 – фазовая скорость волны;
– фазовая скорость волны; 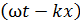 – фаза плоской волны.
– фаза плоской волны.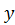
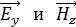 перпендикулярны направлению распространения волны – оси
перпендикулярны направлению распространения волны – оси 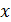 и скорости волны
и скорости волны 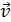 . Напряженности полей
. Напряженности полей 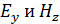 колеблются в одинаковой фазе, при этом их максимумы
колеблются в одинаковой фазе, при этом их максимумы 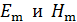 достигаются одновременно и в одной и той же точке пространства; также и нули (
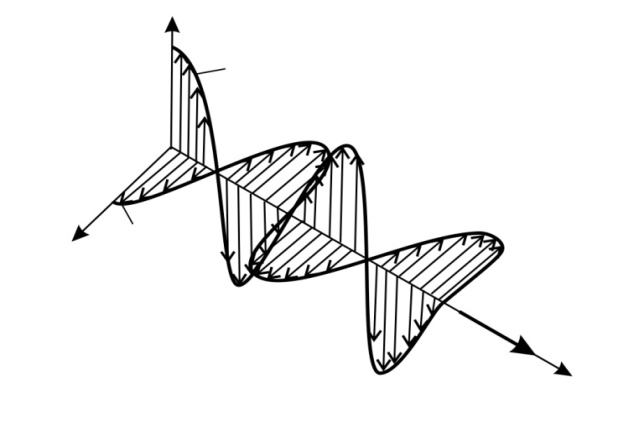
достигаются одновременно и в одной и той же точке пространства; также и нули ( 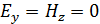 ) достигаются одновременно. Мгновенная (в данный момент времени
) достигаются одновременно. Мгновенная (в данный момент времени 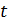 ) картина полей в ЭМВ, бегущей вдоль оси
) картина полей в ЭМВ, бегущей вдоль оси 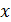 , показана на рис. 4.
, показана на рис. 4.
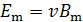 , (11)
где
, (11)
где 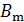 – амплитуда индукции магнитного поля;
– амплитуда индукции магнитного поля; 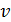 – фазовая скорость ЭМВ. В вакууме (и в воздухе) ее величина равна скорости света:
– фазовая скорость ЭМВ. В вакууме (и в воздухе) ее величина равна скорости света:
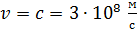 .
.
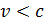 , зависит от свойств среды и определяется следующей формулой:
, зависит от свойств среды и определяется следующей формулой: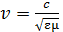 ,
,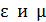 – диэлектрическая и магнитная проницаемости среды.
– диэлектрическая и магнитная проницаемости среды.
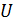
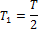
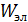
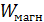
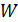
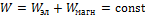
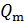
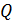
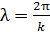 ;
;
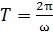 ;
;