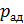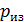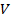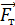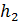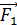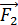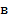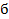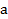1. При использовании первого закона термодинамики: 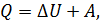 – а также при вычислении работы газа A и количества переданной теплоты
– а также при вычислении работы газа A и количества переданной теплоты 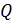 нужно обращать внимание на знаки величин.
нужно обращать внимание на знаки величин.
Количество теплоты положительно (т. е. 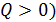 , если система получает энергию в виде теплоты; при этом, согласно определительной формуле
, если система получает энергию в виде теплоты; при этом, согласно определительной формуле 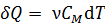 , величина приращения температуры
, величина приращения температуры 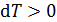 , т. е. температура газа увеличивается.
, т. е. температура газа увеличивается.
Аналогично определяется знак приращения внутренней энергии 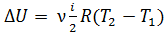 ; из этой формулы следует, что
; из этой формулы следует, что 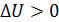 , если
, если 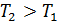 , т. е. приращение внутренней энергии положительно (величина U возрастает), если при переходе газа из 1-го состояния во 2-е увеличивается температура газа. И наоборот, если
, т. е. приращение внутренней энергии положительно (величина U возрастает), если при переходе газа из 1-го состояния во 2-е увеличивается температура газа. И наоборот, если 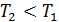 , т. е. температура газа понижается, то величина
, т. е. температура газа понижается, то величина 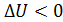 , так как внутренняя энергия газа уменьшается.
, так как внутренняя энергия газа уменьшается.
Знак работы следует из определительной формулы для элементарной работы газа 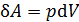 ; так как давление газа
; так как давление газа 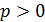 , то знак работы
, то знак работы 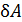 совпадает со знаком приращения объема. Величина
совпадает со знаком приращения объема. Величина 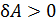 , если
, если 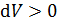 (объем газа увеличивается в ходе процесса), т. е. работа газа
(объем газа увеличивается в ходе процесса), т. е. работа газа 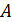 положительна при расширении газа. И наоборот, при
положительна при расширении газа. И наоборот, при 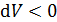 (объем уменьшается) работа
(объем уменьшается) работа 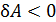 , т. е. при сжатии работа газа отрицательна; в этом случае внешние силы совершают положительную работу.
, т. е. при сжатии работа газа отрицательна; в этом случае внешние силы совершают положительную работу.
2. Полезно, а в ряде задач и необходимо изображать график процесса в координатах 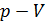 , контролируя изменение параметров газа с помощью уравнения состояния идеального газа
, контролируя изменение параметров газа с помощью уравнения состояния идеального газа
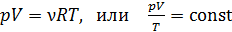 .
.
Из последнего уравнения объединенного газового закона легко получить газовые законы для изопроцессов:
1) изотермический процесс ( 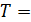 const):
const): 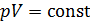 , или
, или 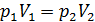 ;
;
2) изобарический процесс ( 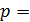 const):
const): 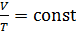 , или
, или 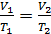 ;
;
3) изохорический процесс ( 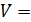 const):
const): 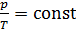 , или
, или 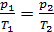 .
.
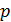
|
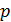
|
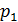
|
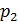
|
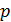
|
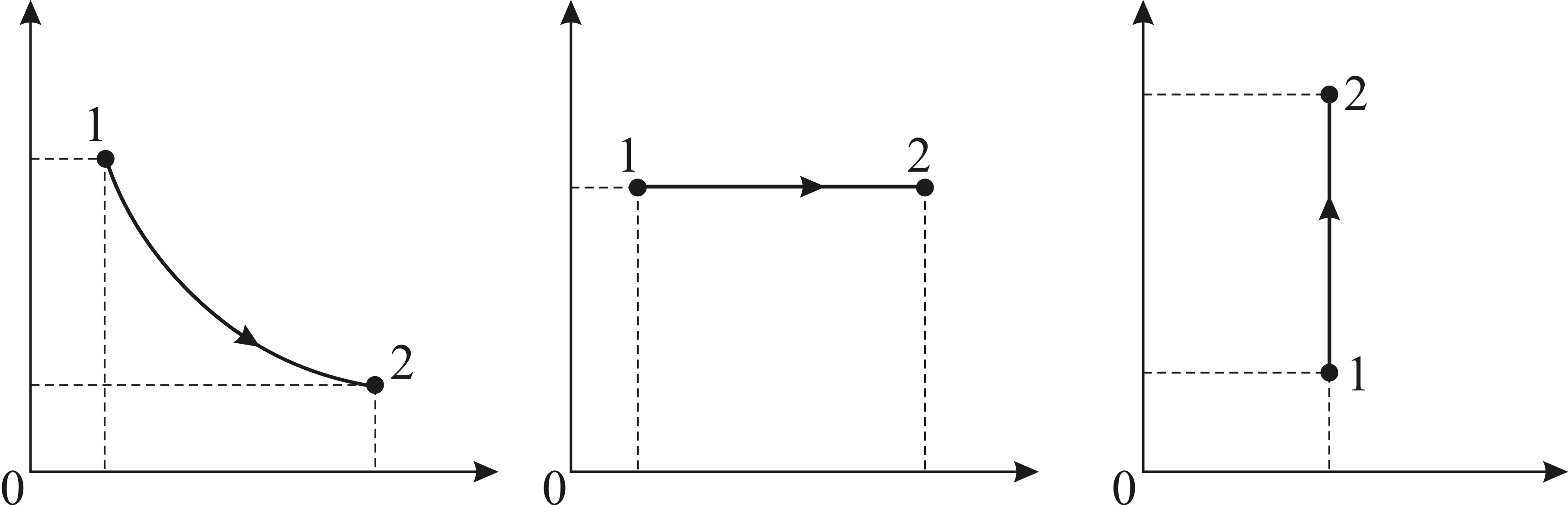
Рис. 21. График Рис. 22. График Рис. 23. График изотермы: (1–2) – изобары: расширение изохоры: (1–2) – расширение газа газа при нагреве нагрев газа 4) уравнение адиабатного процесса
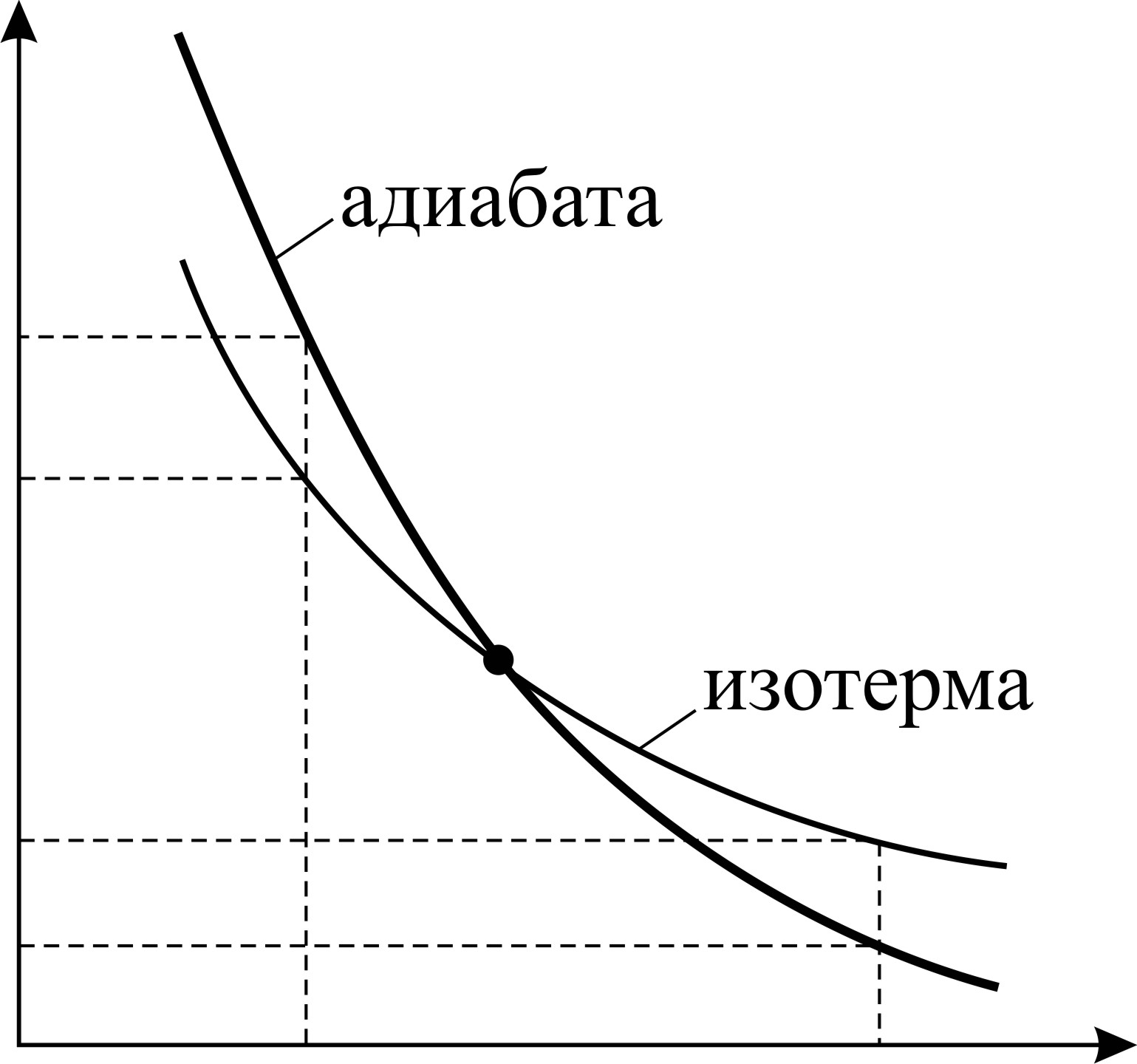
Так как показатель адиабаты
1 адиабата идет ниже изотермы и при одинаковом объеме
и адиабатного процесса |
О2: 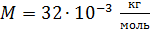 ; ;
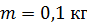 ; ;
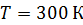 ; ;
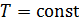 ; ;
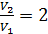 . .
|
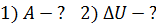
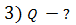
|
Задача 26. При изотермическом расширении кислорода массой 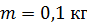 при температуре
при температуре 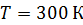 его объем увеличился в два раза. Определите 1) совершенную газом работу
его объем увеличился в два раза. Определите 1) совершенную газом работу 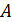 , 2) изменение внутренней энергии газа
, 2) изменение внутренней энергии газа 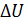 , 3) количество теплоты
, 3) количество теплоты 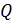 , полученное газом.
, полученное газом.
Дано Решение
|
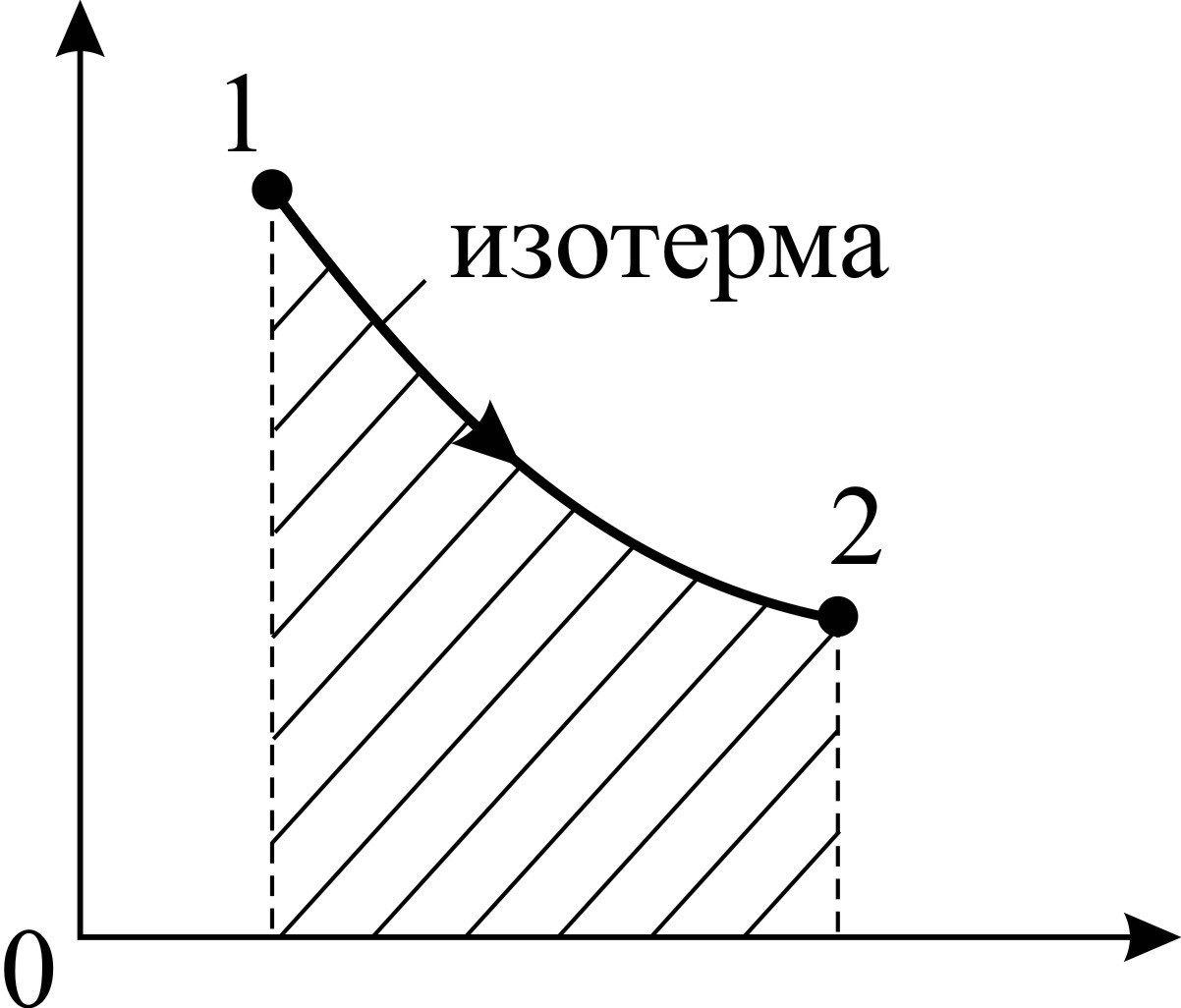
Рис. 25 |
|
1) Работа, совершенная газом, вычисляется по следующей формуле:
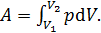 (1)
(1)
Из графика процесса (рис. 25) видно, что по мере увеличения объема газа его давление снижается в соответствии с уравнением процесса 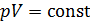 . Следовательно, в формуле (1) под знаком интеграла содержатся две переменные:
. Следовательно, в формуле (1) под знаком интеграла содержатся две переменные: 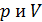 . Выразим давление
. Выразим давление 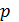 через объем
через объем 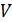 из уравнения состояния идеального газа
из уравнения состояния идеального газа
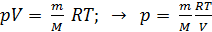 . (2)
. (2)
Подставим выражение (2) в формулу (1), вынесем постоянные величины за знак интеграла и проинтегрируем:
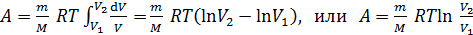 . (3)
. (3)
Вычислим работу газа по формуле (3):
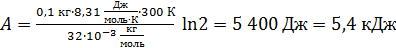 .
.
2) Внутренняя энергия газа 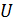 зависит от его температуры, а ее приращение
зависит от его температуры, а ее приращение
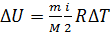 , так как
, так как 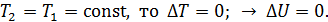
3) Количество теплоты, полученной газом в изотермическим процессе, найдем по формуле первого закона термодинамики:
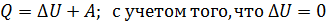 , имеем
, имеем 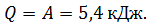
Задача 27. Какая доля 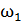 количества теплоты
количества теплоты 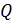 , подводимого к идеальному газу в изобарном процессе, расходуется на увеличение внутренней энергии газа
, подводимого к идеальному газу в изобарном процессе, расходуется на увеличение внутренней энергии газа 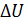 и какая доля
и какая доля 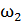 – на работу A расширения газа? Рассмотрите три случая: 1) газ одноатомный, 2) газ двухатомный, 3) газ трехатомный.
– на работу A расширения газа? Рассмотрите три случая: 1) газ одноатомный, 2) газ двухатомный, 3) газ трехатомный.
|
 . .
|
|
1) одноатомный газ: 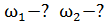 2) двухатомный газ:
2) двухатомный газ: 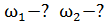 3) трехатомный газ:
3) трехатомный газ: 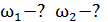
|
|
Рис. 26 |
График изобарного процесса представлен на рис. 26. Количество теплоты 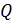 , поглощаемое газом при изобарном нагревании, определяется формулой
, поглощаемое газом при изобарном нагревании, определяется формулой
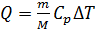 , (1)
, (1)
где 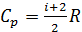 – молярная теплоемкость газа при постоянном давлении. С учетом формулы для величины
– молярная теплоемкость газа при постоянном давлении. С учетом формулы для величины 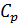 уравнение (1) принимает вид:
уравнение (1) принимает вид:
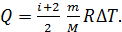 (2)
(2)
Найдем долю энергии 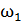 . Приращение внутренней энергии
. Приращение внутренней энергии 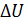 определим по формуле
определим по формуле
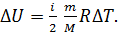 (3)
(3)
Следовательно, доля подводимой энергии, которая идет на увеличение внутренней энергии газа, с учетом формул (2) и (3), после сокращения в отношении сомножителя 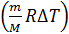 представится формулой:
представится формулой:
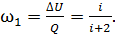 (4)
(4)
Найдем долю энергии 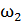 . Работа, совершаемая газом при изобарном расширении, определяется следующим образом:
. Работа, совершаемая газом при изобарном расширении, определяется следующим образом:
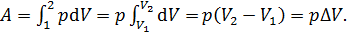 (5)
(5)
В соответствии с полученной формулой (5) величина работы A равна площади прямоугольника на графике процесса (см. рис. 24). Используем уравнение состояния идеального газа для состояний 1 и 2 в изобарном процессе:
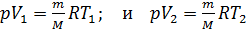 .
.
Вычитая из второго уравнения первое, получаем связь приращений параметров газа в следующем виде:
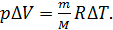 (6)
(6)
С учетом выражения (6) формулу работы (5) запишем так:
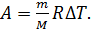 (7)
(7)
Рассчитаем долю энергии, которая расходуется на работу, используя формулы (2) и (7):
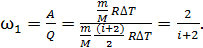 (8)
(8)
Привлекая первый закон термодинамики 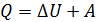 , найдем
, найдем
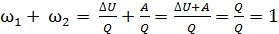 ,
,
и проверим полученные формулы (4) и (8):
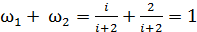 .
.
Следовательно, полученные расчетные формулы (4) и (8) верны.
Вычисляем по этим формулам значения  :
:
1) одноатомный газ: число степеней свободы молекулы 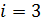 ,
,
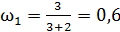 ;
; 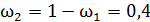 ;
;
2) двухатомный газ: 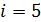 ,
,
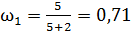 ;
; 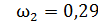 ;
;
3) трехатомный газ: 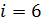 ,
,
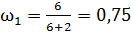 ;
; 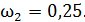
|
|
|
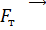
|
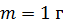 . Какое количество теплоты требуется для нагрева этого газа на
. Какое количество теплоты требуется для нагрева этого газа на 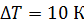 ? На какую высоту при этом поднимется поршень? Масса поршня
? На какую высоту при этом поднимется поршень? Масса поршня 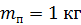 , его площадь
, его площадь  Воздух снаружи находится под давлением
Воздух снаружи находится под давлением 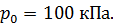
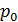
|
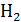 : M : M 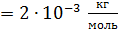 ; ;
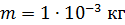 ; ;
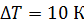 ; ;
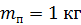 ; ;
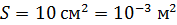 ; ;
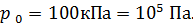
|
|
1) 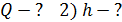
|
|
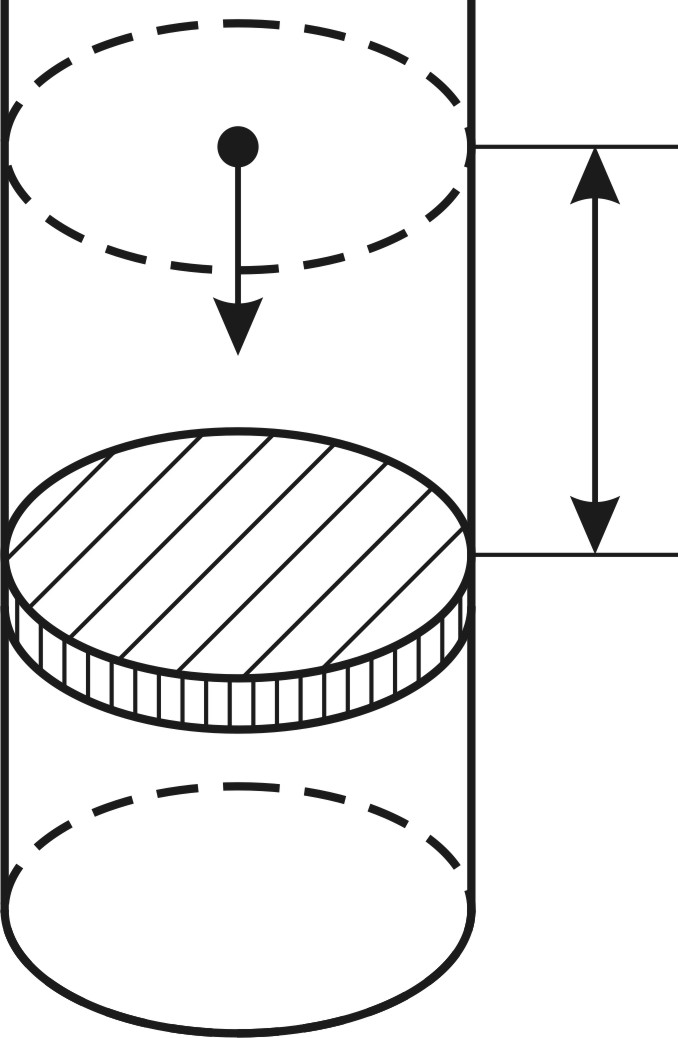
Рис. 27 |
Так как поршень над газом находится в состоянии покоя, то сила давления F на поршень со стороны водорода (рис. 27) уравновешивается двумя силами – силой давления  внешнего газа на поршень и силой тяжести поршня
внешнего газа на поршень и силой тяжести поршня 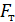 :
:
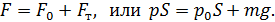
Следовательно, давление водорода в цилиндре под поршнем
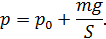
При нагревании газа это равенство выполняется, так как нагрев в условиях свободного расширения газа происходит изобарно при давлении водорода
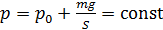 . (1)
. (1)
1) В изобарном процессе количество подведенной для нагрева газа теплоты определяется следующей формулой:
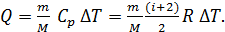 (2)
(2)
В этой формуле число степеней свободы двухатомной молекулы водорода 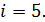 Вычисляем
Вычисляем
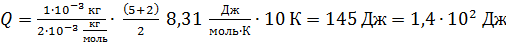 .
.
2) Найдем перемещение поршня h . Высота, на которую поднимется поршень, определяется приращением объема газа
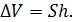 (3)
(3)
Приращение объема газа 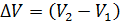 определим, записывая уравнение состояния идеального газа для двух состояний водорода – 1 и 2:
определим, записывая уравнение состояния идеального газа для двух состояний водорода – 1 и 2:
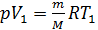 ; и
; и 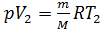 .
.
Вычитая из второго уравнения первое, получаем, что
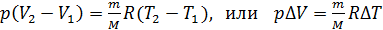 . (4)
. (4)
Из уравнения (4) выразим величину приращения объема газа 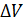 :
:
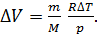 (5)
(5)
Приравнивая значения 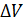 по формулам (3) и (5) и учитывая выражение (1) для давления водорода, получим расчетную формулу определяемой величины h в виде
по формулам (3) и (5) и учитывая выражение (1) для давления водорода, получим расчетную формулу определяемой величины h в виде
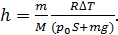 (6)
(6)
Вычислим перемещение поршня при нагреве газа по формуле (6):
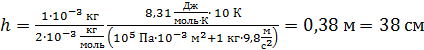 .
.
Задача 29. При адиабатном сжатии воздуха в цилиндрах двигателя внутреннего сгорания давление возрастает от значения 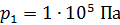 до величины
до величины 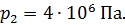 Начальная температура воздуха
Начальная температура воздуха 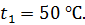 Определите температуру газа
Определите температуру газа 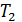 в конце сжатия.
в конце сжатия.
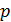
|
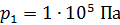 ; ;
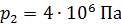 ; ;
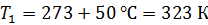 . .
| |
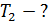
|
|
Рис. 28 |
В адиабатном процессе параметры газа связаны уравнением Пуассона:
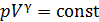 , (1)
, (1)
и соответствующая кривая адиабатного сжатия приведена на рис. 28. Уравнение (1) запишем для двух состояний газа: 1 – в начале и 2 – в конце адиабатного сжатия воздуха:
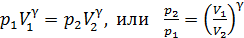 . (2)
. (2)
Выразим неизвестное отношение объемов через заданные параметры, используя уравнение состояния идеального газа, – оно справедливо для состояния газа в любом равновесном процессе:
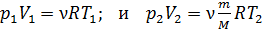 .
.
Выразим отношение 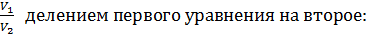
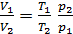 ,
,
и подставим в уравнение адиабатного процесса (2):
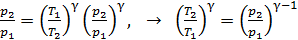 ,
,
затем определяем отношение температур
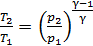 ,
, 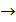
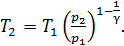 (3)
(3)
Вычислим показатель степени в уравнении (3). Сначала определим показатель адиабаты 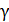 , учитывая, что двухатомные молекулы воздуха (O2 и N2) имеют
, учитывая, что двухатомные молекулы воздуха (O2 и N2) имеют 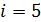 степеней свободы:
степеней свободы:
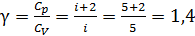 .
.
Величина 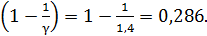
Вычисляем температуру воздуха в конце адиабатного сжатия по формуле (3):
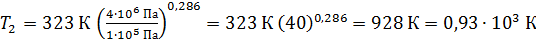 .
.
Задача 30. В цилиндрическом сосуде высотой 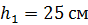 и площадью основания
и площадью основания 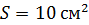 под невесомым поршнем площадью
под невесомым поршнем площадью 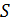 находится газ при нормальных условиях. Когда на поршень положили груз массой
находится газ при нормальных условиях. Когда на поршень положили груз массой 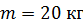 , поршень опустился на
, поршень опустился на 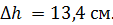 Считая сжатие газа адиабатным, найдите показатель адиабаты
Считая сжатие газа адиабатным, найдите показатель адиабаты 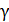 .
.
Дано Решение
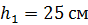 ; ;
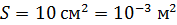 ; ;
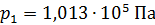 ; ;
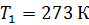 ; ;
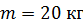 ; ;
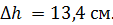
| |
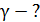
|
Рис. 29 |
|
Запишем уравнение адиабатного процесса, связывающее параметры газа в начале и в конце сжатия:
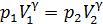 . (1)
. (1)
График адиабаты приведен в решении предыдущей задачи (см. рис. 28). Представим уравнение (1) в виде, удобном для расчета величины 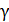 :
:
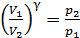 .
.
Логарифмируя это равенство, получаем следующее выражение:
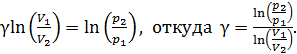 (2)
(2)
Для определения давления 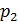 запишем условие равновесия поршня в конце адиабатного сжатия газа (рис. 29):
запишем условие равновесия поршня в конце адиабатного сжатия газа (рис. 29):
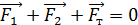 , (3)
, (3)
где 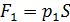 – сила давления внешнего газа на поршень (давление
– сила давления внешнего газа на поршень (давление 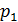 снаружи осталось таким же, каким было до помещения груза на поршень);
снаружи осталось таким же, каким было до помещения груза на поршень); 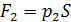 – сила давления газа, находящегося в сосуде;
– сила давления газа, находящегося в сосуде; 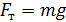 – сила тяжести груза, помещенного на поршень.
– сила тяжести груза, помещенного на поршень.
Запишем проекцию уравнения (3) на ось y (см. рис. 29), подставим значения сил и выразим давление 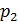 :
:
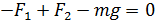 ;
; 
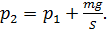
Разделив последнее равенство на 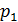 , получим отношение давлений в виде:
, получим отношение давлений в виде:
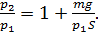 (4)
(4)
Определим объемы газа в состояниях 1 и 2:
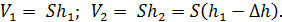
Запишем величину отношения объемов газа
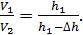 (5)
(5)
Подставим в формулу (2) значения отношений давлений и объемов газа в состояниях 1 и 2, используя выражения (4) и (5), и получим расчетную формулу величины 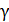 :
:
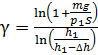 .
.
Вычислим показатель адиабаты газа:
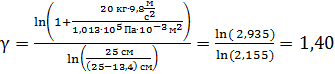 .
.
Полученное значение показателя адиабаты газа, находящегося в сосуде, равно величине 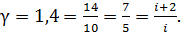 Следовательно, число степеней свободы молекулы газа
Следовательно, число степеней свободы молекулы газа 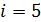 и адиабатный процесс происходил с двухатомным газом.
и адиабатный процесс происходил с двухатомным газом.
Задача 31. Идеальная тепловая машина работает по циклу Карно. Температура нагревателя 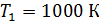 , температура холодильника
, температура холодильника 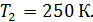 Определите термический КПД цикла η, работу газа при изотермическом расширении
Определите термический КПД цикла η, работу газа при изотермическом расширении 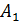 и работу
и работу 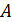 , которую совершает газ за один цикл, если при изотермическом сжатии совершена работа
, которую совершает газ за один цикл, если при изотермическом сжатии совершена работа 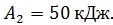
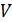
|
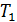
|
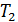
|
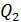
|
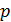
|
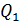
|
|
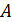
|
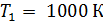 ; ;
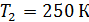 ; ;
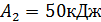 . .
|
1) 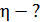 2)
2) 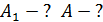
|
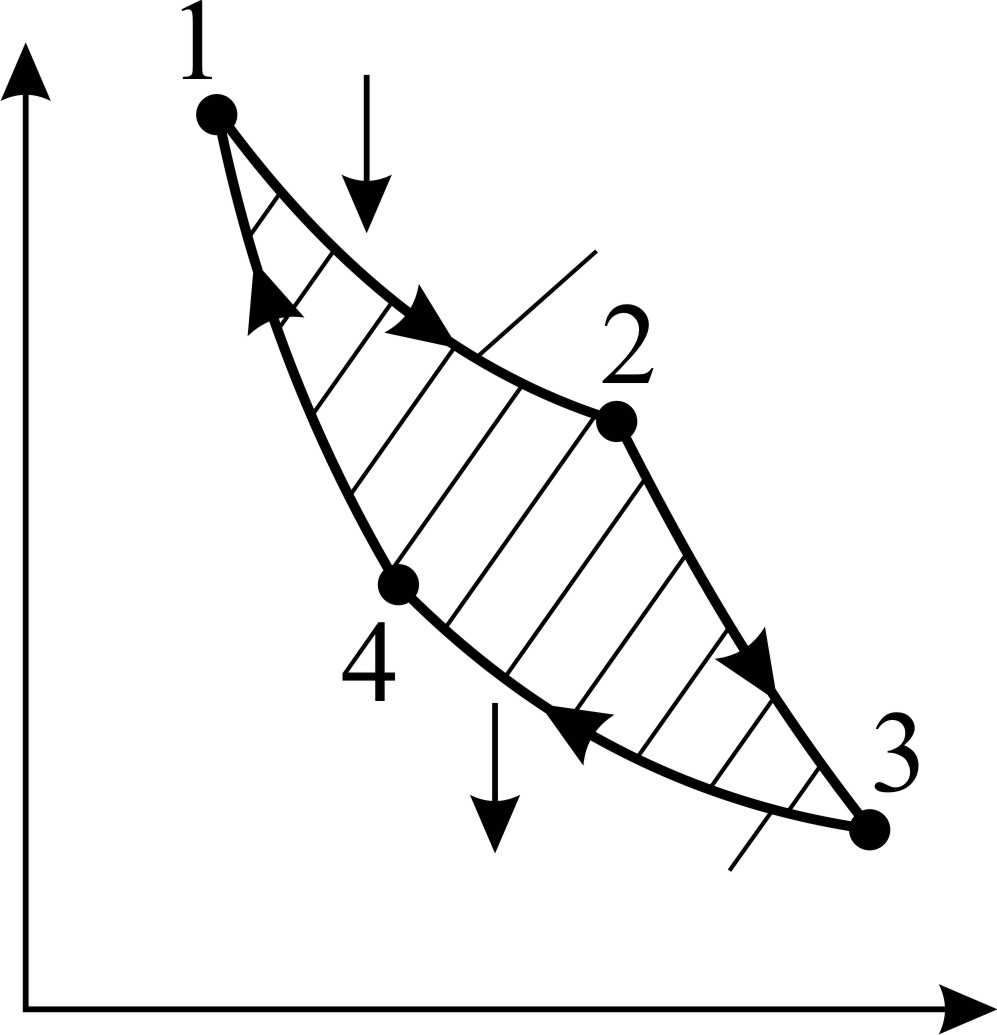 Рис. 30
Рис. 30
|
1) Термический коэффициент полезного действия 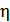 идеальной тепловой машины, работающей по циклу Карно, не зависит от природы газа, совершающего работу, и определяется только температурами нагревателя (
идеальной тепловой машины, работающей по циклу Карно, не зависит от природы газа, совершающего работу, и определяется только температурами нагревателя ( 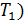 и холодильника (
и холодильника ( 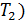 :
:
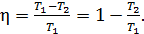 (1)
(1)
Вычислим величину КПД:  , или
, или 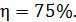
2) С другой стороны, термический КПД любой тепловой машины, работающей циклически:
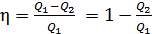 , (2)
, (2)
где 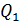 – количество теплоты, подведенной за цикл к газу от нагревателя, в данной задаче – при изотермическом расширении 1–2 (рис. 30);
– количество теплоты, подведенной за цикл к газу от нагревателя, в данной задаче – при изотермическом расширении 1–2 (рис. 30); 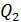 – количество теплоты, отданной газом холодильнику при изотермическом сжатии 3–4.
– количество теплоты, отданной газом холодильнику при изотермическом сжатии 3–4.
Соотношение работы газа и количества теплоты в этих процессах соответствует первому закону термодинамики:
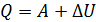 , (3)
, (3)
где 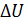 – приращение внутренней энергии газа:
– приращение внутренней энергии газа: 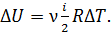 Так как в изотермических процессах
Так как в изотермических процессах 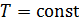 , то приращение температуры
, то приращение температуры 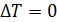 , следовательно, и
, следовательно, и 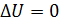 . При этом уравнение (3) для изотермического процесса принимает следующий вид:
. При этом уравнение (3) для изотермического процесса принимает следующий вид:
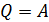 . (4)
. (4)
Запишем данную формулу первого закона термодинамики для процессов изотермического расширения 1–2 и изотермического сжатия 3–4 соответственно
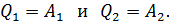 (5)
(5)
Подставим эти величины 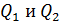 в формулу (2) для термического КПД:
в формулу (2) для термического КПД:
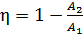 ;
; 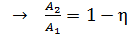 ;
; 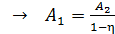 .
.
Вычислим работу газа при изотермическом расширении:
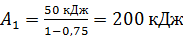 .
.
Для определения работы газа за весь цикл есть два способа:
а) с использованием формулы термического КПД:
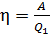 ;
; 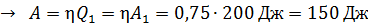 ;
;
б) путем суммирования работы на всех участках цикла:
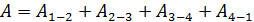 . (6)
. (6)
В этом равенстве величины работы сжатия 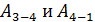 отрицательные. Способ «б», несомненно, более длительный, так как требуется показать, что в адиабатных процессах
отрицательные. Способ «б», несомненно, более длительный, так как требуется показать, что в адиабатных процессах 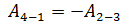 . Это несложно, если учесть, что в адиабатном процессе
. Это несложно, если учесть, что в адиабатном процессе 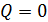 , и первый закон термодинамики (3) имеет следующий вид:
, и первый закон термодинамики (3) имеет следующий вид:
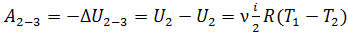 ;
;
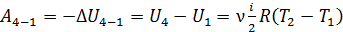 .
.
Сравнивая полученные выражения для работы, видим, что 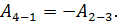 Учтем это равенство в формуле (6) и заменим
Учтем это равенство в формуле (6) и заменим 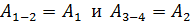 :
:
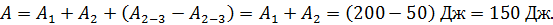
Задача 32. Определите приращение энтропии 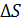 при нагреве льда массой
при нагреве льда массой 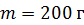 от температуры
от температуры 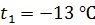 , при плавлении льда, при нагреве полученной воды и превращении ее в пар при
, при плавлении льда, при нагреве полученной воды и превращении ее в пар при 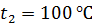 .
.
Дано Решение
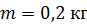 ; ;
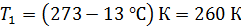 ; ;
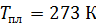 ; ;
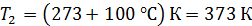 ; ;
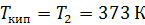 . .
|
|
Приращение энтропии при переходе вещества из состояния 1 в состояние 2 определяется общей формулой:
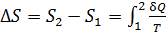 , (1)
, (1)
где 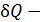 бесконечно малое количество теплоты, переданной веществу при температуре T в обратимом процессе.
бесконечно малое количество теплоты, переданной веществу при температуре T в обратимом процессе.
Величину 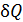 можно представить двумя формулами: а) при нагреве (охлаждении) тела на бесконечно малое приращение температуры
можно представить двумя формулами: а) при нагреве (охлаждении) тела на бесконечно малое приращение температуры 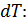
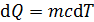 , (2)
, (2)
где c – удельная теплоемкость вещества; m – его масса;
б) при фазовом превращении, протекающем при постоянной температуре:
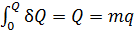 , (3)
, (3)
где 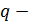 удельная теплота фазового перехода.
удельная теплота фазового перехода.
В зависимости от того, как рассчитывается величина 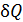 в подинтегральном выражении в формуле (1), данный интеграл находится как сумма четырех слагаемых:
в подинтегральном выражении в формуле (1), данный интеграл находится как сумма четырех слагаемых:
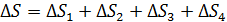 . (4)
. (4)
Здесь 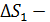 увеличение энтропии при нагреве льда до температуры плавления;
увеличение энтропии при нагреве льда до температуры плавления; 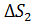 – приращение энтропии при плавлении льда;
– приращение энтропии при плавлении льда; 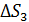 – увеличение энтропии при нагреве воды;
– увеличение энтропии при нагреве воды; 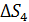 – увеличение энтропии при превращении воды в пар.
– увеличение энтропии при превращении воды в пар.
Рассчитаем величины этих слагаемых приращения энтропии.
1) Нагрев льда:
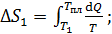 по формуле (2):
по формуле (2): 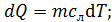
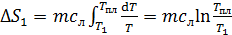 ,
,
где 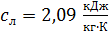 – удельная теплоемкость льда.
– удельная теплоемкость льда.
Вычисляем: 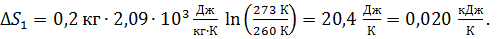
2) Плавление льда происходит при постоянной температуре, равной 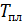 , которую выносим за знак интеграла:
, которую выносим за знак интеграла:
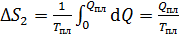 ; по формуле (3):
; по формуле (3): 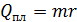 ;
; 
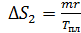 ,
,
где 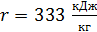 – удельная теплота плавления льда.
– удельная теплота плавления льда.
Вычисляем: 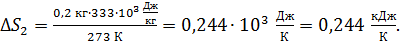
3) Нагрев воды:
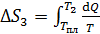 , где
, где 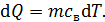
Расчет, аналогичный таковому для 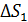 , дает формулу
, дает формулу
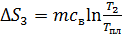 ,
,
где 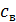 – удельная теплоемкость воды.
– удельная теплоемкость воды.
Молярная теплоемкость воды 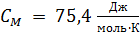 , вычислим ее удельную теплоемкость
, вычислим ее удельную теплоемкость 
Вычисляем приращение энтропии
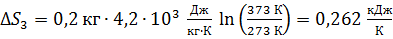 .
.
4) Превращение воды в пар, по условию задачи, происходит при температуре кипения: 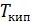 при этом постоянна, поэтому расчет аналогичен таковому для
при этом постоянна, поэтому расчет аналогичен таковому для 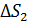 . Результат расчета:
. Результат расчета:
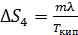 .
.
Здесь 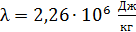 – удельная теплота парообразования воды.
– удельная теплота парообразования воды.
Вычисляем приращение энтропии:
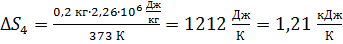 .
.
Согласно выражению (4), суммируем приращения энтропии вещества в четырех последовательных процессах:
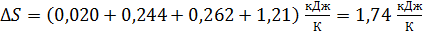 .
.
Сравнивая слагаемые в последнем выражении, отметим, что энтропия вещества существенно возрастает при фазовом переходе из кристаллического в жидкое состояние, но еще более она возрастает при превращении жидкости в пар.
Задача 33. Определите изменение энтропии 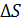 смеси, состоящей из гелия массой
смеси, состоящей из гелия массой 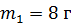 и азота массой
и азота массой 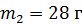 , при переходе от объема
, при переходе от объема 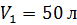 и давления
и давления 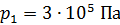 к объему
к объему 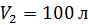 и давлению
и давлению 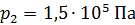 .
.
Дано Решение
He: 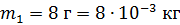 ; ; 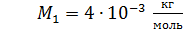 ; ;
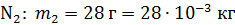 ; ;
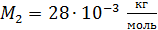 ; ;
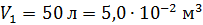 ; ;
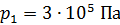 ; ;
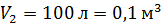 ; ;
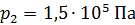 . .
|
|
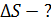
|
Приращение энтропии 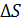 при переходе вещества из состояния 1 в состояние 2 определяется формулой
при переходе вещества из состояния 1 в состояние 2 определяется формулой
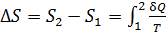 , (1)
, (1)
где 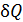 – бесконечно малое количество теплоты, переданной газу в обратимом процессе при температуре
– бесконечно малое количество теплоты, переданной газу в обратимом процессе при температуре 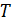 . Величину
. Величину 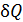 для газа обычно выражают через молярную теплоемкость
для газа обычно выражают через молярную теплоемкость 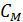 и бесконечно малое приращение температуры
и бесконечно малое приращение температуры 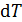 :
:
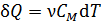 , (2)
, (2)
где 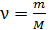 – число молей вещества.
– число молей вещества.
Молярные теплоемкости идеального газа известны для двух процессов передачи теплоты: изобарного и изохорного – соответственно 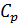 и
и 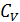 . Поэтому осуществим переход смеси газов из состояния 1 в состояние 2 изобарным расширением а-б и последующим изохорным охлаждением б-в (рис. 31). При этом определяемое приращение энтропии
. Поэтому осуществим переход смеси газов из состояния 1 в состояние 2 изобарным расширением а-б и последующим изохорным охлаждением б-в (рис. 31). При этом определяемое приращение энтропии
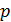
|
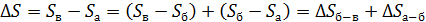 . (3)
. (3)
|
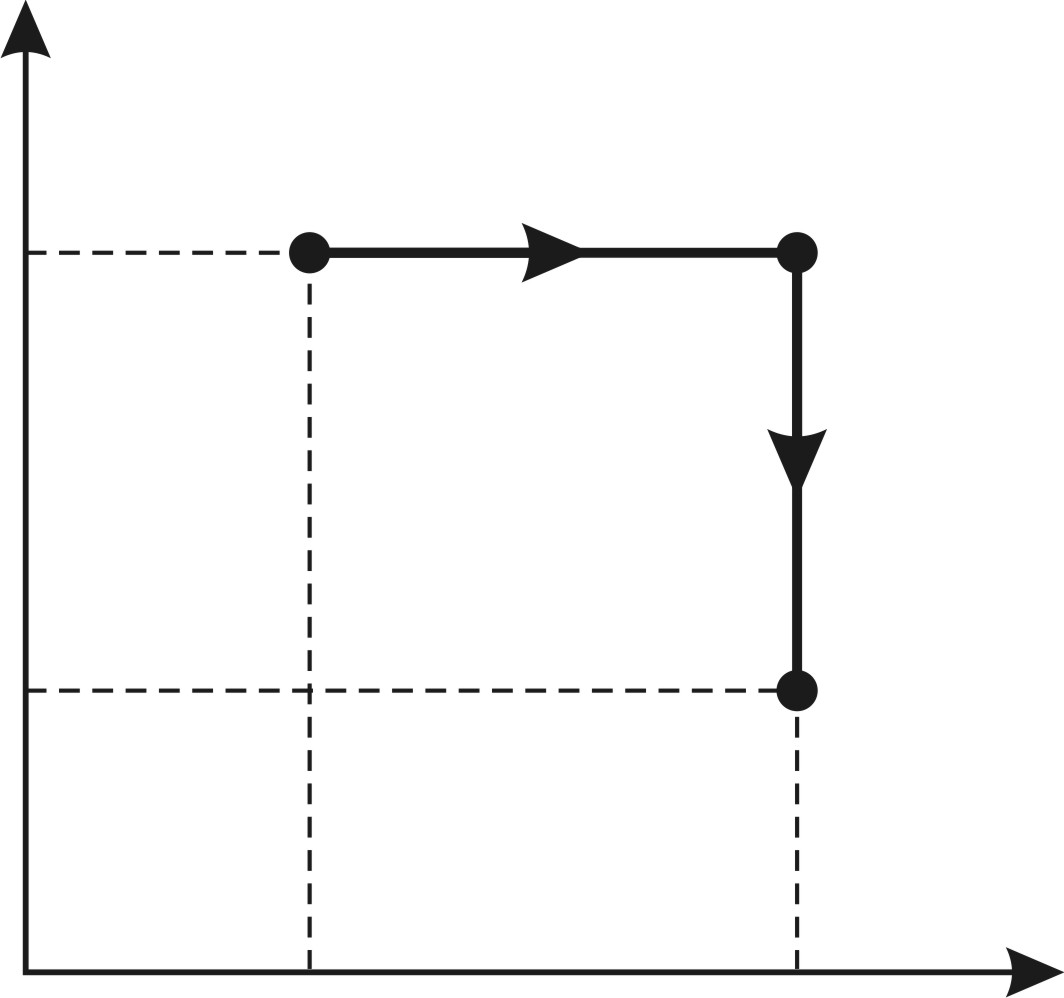
Рис. 31 |
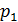
|
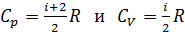 , (4)
, (4)
|
 для одноатомной молекулы гелия и
для одноатомной молекулы гелия и  для двухатомной молекулы азота. Соответственно, теплоемкости, а следовательно, и изменение энтропии этих компонентов смеси газов, согласно формулам (1), (2) и (4) вычисляются различно.
для двухатомной молекулы азота. Соответственно, теплоемкости, а следовательно, и изменение энтропии этих компонентов смеси газов, согласно формулам (1), (2) и (4) вычисляются различно.
Таким образом, необходимо рассматривать данную смесь газов как термодинамическую систему, состоящую из двух частей (подсистем): 1-й – гелия и 2-й – азота. Согласно свойству аддитивности, приращение энтропии этой системы
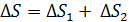 . (5)
. (5)
1) В изобарном процессе а–б вычисляем приращение энтропии k-го компонента смеси газов с использованием формул (1), (2) и (4):
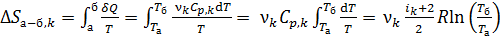 .
.
Так как, согласно уравнению изобарного процесса 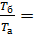
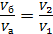 , то
, то
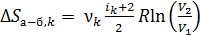 . (6)
. (6)
2) В изохорном процессе б–в таким же образом получаем
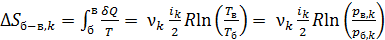 , (7)
, (7)
так как по уравнению изохорного процесса отношение 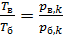 .
.
В формуле (7) величины 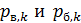 – парциальные давления k -го компонента смеси газов. Напомним, что парциальным называется такое давление компонента смеси, которое он оказывал бы, если бы он один занимал весь объем смеси при той же температуре. Запишем уравнение состояния идеального газа для каждого компонента смеси, используя величины парциального давления
– парциальные давления k -го компонента смеси газов. Напомним, что парциальным называется такое давление компонента смеси, которое он оказывал бы, если бы он один занимал весь объем смеси при той же температуре. Запишем уравнение состояния идеального газа для каждого компонента смеси, используя величины парциального давления 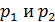 :
:
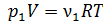 ; (8)
; (8) 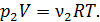 (9)
(9)
Сложим эти уравнения и учтем закон Дальтона для давления смеси идеальных газов: 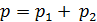 . При этом получаем
. При этом получаем
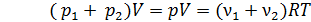 . (10)
. (10)
Используя уравнения (8) и (10), путем деления первого на второе находим отношение давлений 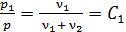 , где
, где 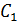 – постоянная для данной смеси газов, следовательно,
– постоянная для данной смеси газов, следовательно, 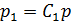 , т. е. парциальное давление каждого компонента смеси пропорционально давлению смеси газов. При этом
, т. е. парциальное давление каждого компонента смеси пропорционально давлению смеси газов. При этом
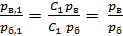 , (11)
, (11)
т. е. для каждого компонента смеси отношение парциальных давлений, входящих в формулу (7), равно отношению давлений газовой смеси в состояниях в и б, так как аналогичное равенству (11) соотношение давлений можно получить и для второго компонента смеси – азота.
С учетом этого уравнение (7) для приращения энтропии k -го компонента смеси в изохорном процессе принимает следующий вид:
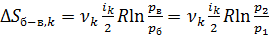 . (12)
. (12)
С помощью уравнения (3): 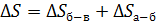 , – используя равенства (6) и (12), получим расчетные формулы для каждого компонента смеси:
, – используя равенства (6) и (12), получим расчетные формулы для каждого компонента смеси:
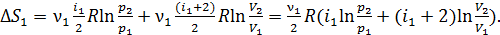 (13)
(13)
Аналогично
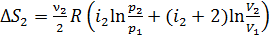 . (14)
. (14)
Здесь 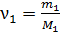 и
и 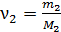 – количество вещества первого и второго компонентов смеси.
– количество вещества первого и второго компонентов смеси.
Вычислим эти приращения энтропии компонентов смеси газа:
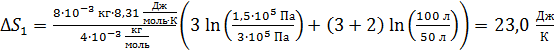 ;
;
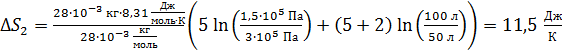 .
.
Используя свойство аддитивности энтропии, найдем приращение энтропии смеси газов по уравнению (5), как сумму приращений энтропии двух частей системы – 1-го и 2-го компонентов смеси:
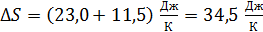 .
.
Задача 34. Водород массой 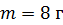 нагревают от
нагревают от 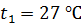 до
до 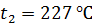 : 1) изохорно, 2) изобарно, 3) адиабатно. Определите для этих процессов приращение энтропии
: 1) изохорно, 2) изобарно, 3) адиабатно. Определите для этих процессов приращение энтропии 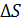 , приращение внутренней энергии
, приращение внутренней энергии 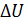 и работу газа
и работу газа 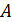 .
.
Дано Решение
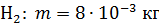 ; ;
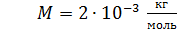 ; ;
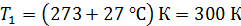 ; ;
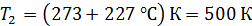 ;
Нагрев: 1) изохорный,
2) изобарный, 3) адиабатный. ;
Нагрев: 1) изохорный,
2) изобарный, 3) адиабатный.
|
В процессах 1, 2 и 3:
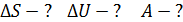
|
Внутренняя энергия идеального газа – функция состояния, зависящая от количества газа 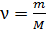 , структуры молекул (число i) и от температуры газа:
, структуры молекул (число i) и от температуры газа:
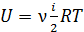 .
.
Поэтому ее приращение
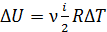 (1)
(1)
одинаково во всех трех процессах, так как в каждом процессе приращение температуры 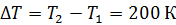 . Принимая, что число степеней свободы двухатомной молекулы водорода
. Принимая, что число степеней свободы двухатомной молекулы водорода 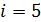 , вычисляем
, вычисляем
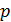
|
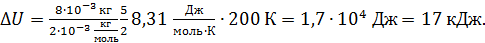
|
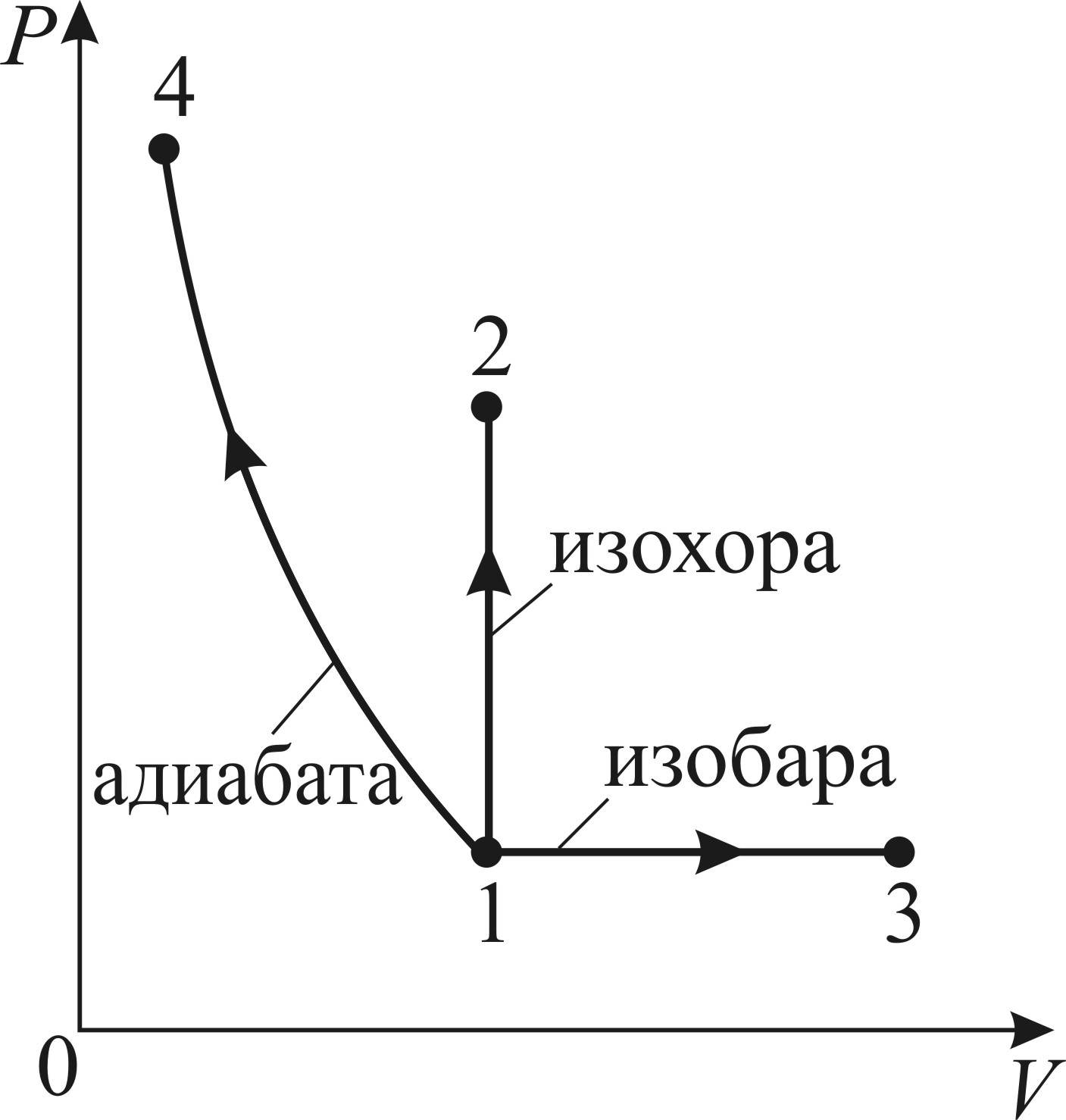
Рис. 32 |
Из графиков рассматриваемых процессов нагрева газа (рис. 32) видно, что параметры газа давление 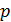 и объем
и объем 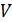 в конечных состояниях 2, 3 и 4 различны во всех трех процессах. Потому энтропия газа, которая так же, как и внутренняя энергия, является функцией состояния, различна:
в конечных состояниях 2, 3 и 4 различны во всех трех процессах. Потому энтропия газа, которая так же, как и внутренняя энергия, является функцией состояния, различна: 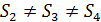 . Следовательно, и приращение энтропии
. Следовательно, и приращение энтропии 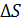 будет различно в этих процессах.
будет различно в этих процессах.
1) Изохорный нагрев газа 1–2.
Приращение энтропии данного количества газа
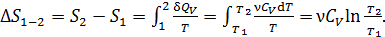 (2)
(2)
Вычисляем величину 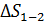 , полагая, что количество газа
, полагая, что количество газа 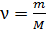 , а молярная теплоемкость при постоянном объеме
, а молярная теплоемкость при постоянном объеме 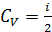 R:
R:
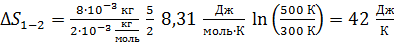 .
.
Работа в изохорном процессе
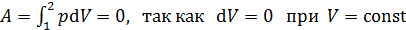 .
.
2) Изобарный нагрев газа 1–3.
Приращение энтропии газа
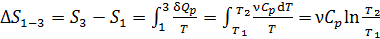 , (3)
, (3)
где 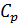 – молярная теплоемкость газа при постоянном давлении:
– молярная теплоемкость газа при постоянном давлении:
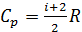 .
.
Сравнивая выражения (2) и (3), видим, что
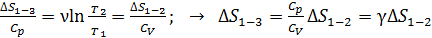 . (4)
. (4)
где 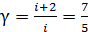 – показатель адиабаты.
– показатель адиабаты.
Вычислим приращение энтропии 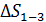 по формуле (4):
по формуле (4):
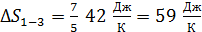 .
.
Работа в изобарном процессе
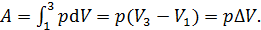 (5)
(5)
Согласно уравнению состояния идеального газа 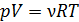 , при
, при 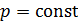 имеем
имеем 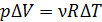 . Подставляя эту величину произведения
. Подставляя эту величину произведения 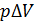 в формулу (5), получаем расчетную формулу работы в изобарном процессе в следующем виде:
в формулу (5), получаем расчетную формулу работы в изобарном процессе в следующем виде:
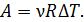 (6)
(6)
Сравнивая формулу работы (6) с формулой (1) для величины 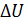 , видим, что
, видим, что 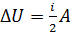 ; следовательно, работа газа
; следовательно, работа газа
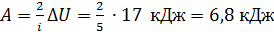 .
.
3) Адиабатный процесс 1–4 происходит без теплообмена газа с окружающей средой: 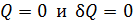 . Соответственно получаем, что приращение энтропии
. Соответственно получаем, что приращение энтропии
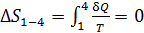 .
.
Следовательно, адиабатный процесс протекает при неизменной энтропии газа: 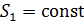 , – это изоэнтропийный процесс.
, – это изоэнтропийный процесс.
Работу газа найдем из формулы первого закона термодинамики:
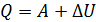 ,
,
которая при 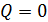 дает величину работы
дает величину работы 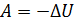 . Согласно этой формуле
. Согласно этой формуле 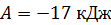 ; работа отрицательна, так как, в соответствии с графиком процесса (см. рис. 32), происходит адиабатное сжатие газа, которое сопровождается его нагревом.
; работа отрицательна, так как, в соответствии с графиком процесса (см. рис. 32), происходит адиабатное сжатие газа, которое сопровождается его нагревом.
ЗАКЛЮЧЕНИЕ
Рассматривая способы решения предложенных задач, видим, что большая часть задач по разделу «механика» решается с использованием законов сохранения.
В связи с этим отметим, что применение законов сохранения представляет собой единственный путь решения физических задач в тех случаях, когда неизвестен закон сил. Это относится к силам, возникающим при неупругой деформации тел, силам мышц человека, силе трения при движении человека, силе трения качения и другим.
Наряду с этим, применение законов сохранения эффективно в тех случаях, когда сила или момент силы изменяется при движении. В таких задачах использование законов динамики требует вычисления интегралов, содержащих более одной переменой, и потому является достаточно сложным. В то же время применение законов сохранения дает сравнительно простой и надежный путь решения.
Следует заметить, что динамические функции механической системы: импульс, момент импульса, механическая энергия, – сохраняются при выполнении определенных условий (замкнутость системы тел, консервативность сил взаимодействия и других). Поэтому выбору того или иного закона сохранения, например, при вращательном движении – ЗСМИ или ЗСМЭ, должен предшествовать анализ сил взаимодействия между телами механической системы и внешних сил.
При рассмотрении термодинамической системы, вычисляя теплоту, переданную газу, и совершенную им работу, в ряде задач использовали первое начало термодинамики – закон сохранения энергии в тепловых процессах.
Отметим, что, как показывают расчеты, выполненные в задачах, величины работы и теплоты различны в разных процессах, т. е. они действительно являются характеристиками процессов, в отличие от функций состояния системы – внутренней энергии и энтропии. Приращения этих величин зависят только от параметров начального и конечного состояния термодинамической системы.
Уравнение состояния идеального газа: уравнение Клапейрона–Менделеева, – является необходимым при решении большей части задач по разделу «Молекулярная физика и термодинамика».
ОГЛАВЛЕНИЕ
Введение …………………………………………………….……….………..3
Список рекомендуемой литературы …….………………….……………….5
Часть 1
МЕХАНИКА
1. Теоретическая часть
1.1 Кинематика поступательного и вращательного движения ..…………..6
1.2. Динамика поступательного движения ………………………………..7
1.3. Динамика вращательного движения ..………………………….………8
1.4. Работа и механическая энергия ….…………………………………......9
1.5. Законы сохранения …………………..……………………..…… . . . . .11
1.5.1. Закон сохранения импульса …...….…..………………………. . . . . 11
1.5.2. Закон сохранения момента импульса .…….…………………...........12
1.5.3. Закон сохранения механической энергии .……..………….………..12
1.6. Механические колебания ……….…….……………………….............13
2. Рекомендации к решению физических задач ………..…..……………..14
3. Примеры решения задач
3.1. Кинематика поступательного и вращательного движения
План решения кинематических задач ….………………………………….15
3.2. Динамика поступательного и вращательного движения
План решения задач с помощью законов динамики …..…..……………..20
3.3. Законы сохранения
План решения задач с использованием законов сохранения: ЗСИ,
ЗСМИ и ЗСМЭ …………………………………………..….……................28
3.4. Механические колебания ………………………………………………41
Часть 2
Дата: 2018-11-18, просмотров: 917.
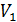
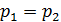
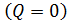 :
: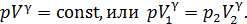
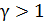 , то кривая адиабатного процесса идет круче, чем изотерма (рис. 24), в уравнении которой показатель степени параметра
, то кривая адиабатного процесса идет круче, чем изотерма (рис. 24), в уравнении которой показатель степени параметра 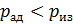 ; тогда, в соответствии с уравнением состояния идеального газа
; тогда, в соответствии с уравнением состояния идеального газа  , т. е. адиабатное расширение газа сопровождается его охлаждением. Аналогично анализируя параметры состояния газа при сжатии, видим, что давление газа
, т. е. адиабатное расширение газа сопровождается его охлаждением. Аналогично анализируя параметры состояния газа при сжатии, видим, что давление газа 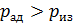 ; соответственно температура газа
; соответственно температура газа  , значит, при
, значит, при