При рассмотрении задач данного раздела вводят понятие материальной точки (МТ). За материальную точку может быть принято любое тело, обладающее массой, размерами которого в условиях данной задачи можно пренебречь. Линия, описываемая материальной точкой в пространстве при ее движении, называется траекторией. Уравнение траектории для плоского движения имеет вид

.

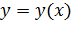  Движение материальной точки в пространстве определяется законом движения, который для МТ может быть задан в виде трех скалярных уравнений:

,

,

,

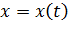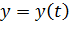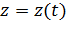либо эквивалентным векторным уравнением:

.

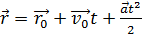  Быстроту движения материальной точки характеризуют средней скоростью

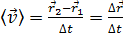или ,

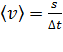где s – путь, пройденный за время 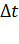, и мгновенной скоростью

,

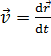которая может быть записана, как любой вектор, в координатной форме:

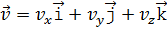,   а  модуль ,

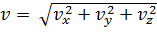где проекции скорости ; ; .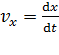

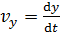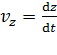  Быстроту изменения скорости при неравномерном движении характеризует ускорение: среднее ускорение

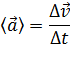
и мгновенное ускорение

.

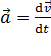С другой стороны,

,

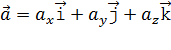где проекции вектора ускорения равны соответствующим производным по времени от проекций скорости: 

; ;                            

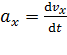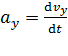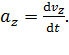
  В криволинейном движении осями координат могут быть касательная к траектории движения материальной точки и нормаль к ней. Орты осей в этом случае 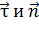. При этом полное ускорение

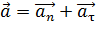,  а его модуль ,

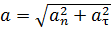где тангенциальное ускорение 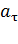 характеризует быстроту изменения модуля скорости и направлено по касательной к траектории:

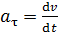, вектор ;

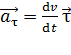нормальное ускорение характеризует быстроту изменения направления скорости и направлено по нормали к центру кривизны траектории:

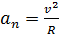, вектор  .

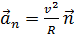Здесь R – радиус кривизны траектории.                                         

  Движение материальной точки по окружности характеризуют угловой скоростью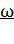

,    

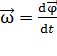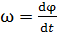
и угловым ускорением

,  .

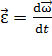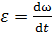  Угловые и линейные величины связаны следующими соотношениями:

;

;

.

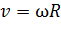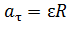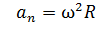  Зная зависимость 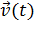 или 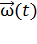, можно найт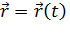и  и :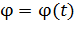

, .

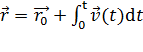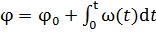Например, для равнопеременного поступательного движения ( 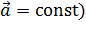и равнопеременного вращения (  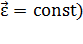) получаем:

, ;

 , .

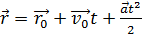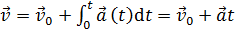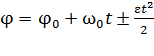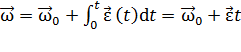1.2. Динамика поступательного движения    

  В основе динамики поступательного движения лежат три закона Ньютона.

  Первый закон Ньютона: всякое тело сохраняет свое состояние покоя или равномерного и прямолинейного движения до тех пор, пока на него не действуют другие тела.

  Второй закон Ньютона (основной закон динамики) гласит, что скорость изменения импульса тела 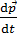равна результирующей всех сил 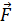, приложенных к телу:

,

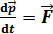где 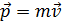  – импульс тела.

  Если 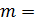 const,  то 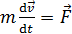;  так как 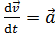, то .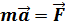

  Третий закон Ньютона: 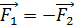, т. е. если первое тело действует на второе с силой 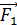, то второе тело действует на первое с силой, равной по модулю, но противоположно направленной.